Математика/ 4.Прикладная математика

К.ф.м.н., доцент Абатов Н.Т.

Костанайский государственный университет имени А.Байтурсынова,

Казахстан

Об решений некоторых тригонометрических уравнений

Выпускники школ затрудняются при решений сложных тригонометрических уравнений, которые встречаются на ЕНТ по математике. Поэтому рассмотрим некоторые сложные тригонометрические уравнения и укажем способ их решения.

№1. Решите уравнение

Решение.

Применяем формулу

Тогда уравнение примет вид:

Воспользуемся формулами:

.

Тогда имеем:

Введем замену Тогда получим квадратное уравнение

Тогда её корни. Произведем обратную замену . Тогда имеем:

a) . Это уравнение не имеет корней.

b)

Итак, корни исходного уравнения.

Ответ:

№2. Решите уравнение

Решение. .

Применяем формулы

Тогда данное уравнение примет вид:

Применяем формулу

Тогда уравнение примет вид:

Применяем формулу

Тогда имеем:

Итак, решение исходного уравнения.

Ответ: .

№3. Решите уравнение

Решение.

Применяем формулу

Тогда данное уравнение примет вид:

Введем замену

Тогда получаем квадратное уравнение её корни.

Производим обратную замену Тогда имеем:

a)

Разделим на обе части уравнения. Тогда имеем:

b)

Обе части данного уравнения умножаем на . Тогда имеем:

Итак,

корни исходного уравнения.

Ответ:

.

№4. Решите уравнение

Решение. Группируем слагаемые:

.

Применяем формулы

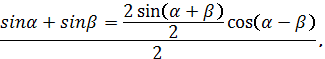
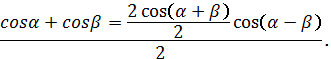
Тогда данное уравнение примет вид:

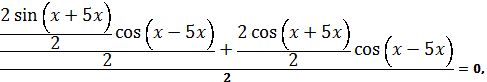
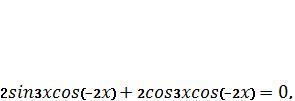
a) , ;

b)

Обе части уравнения разделим на

, .

Итак, , корни исходного уравнения.

Ответ:

Литература

1. Абатов Н.Т. Методы решения задач по математике. Алгебра. Учебное пособие для поступающих в ВУЗы. – Костанай, 1998г.

2. Потапов М.К., Олехник С.Н., Нестеренко Р.В. Конкурсные задачи по математике. Справочное пособие. – Москва, 1995г.