Ìàòåìàòèêà/4.Ïðèêëàäíàÿ ìàòåìàòèêà
O.F. Ryaboshtan,
Ph.D. A.M. Milenin, Ph.D. S.M.
Skofenko
Kharkov National Technical
University of Agriculture after P. Vasilenko
The use of
transition functions for comstructing bypass gas turbine blade
Consider bypass arc passing through the points ![]() and
and ![]() and its derivatives
and its derivatives ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Arc equation can be written as
. Arc equation can be written as
![]() , (1)
, (1)
where the ![]() - transition functions from
- transition functions from ![]() having a bypass nodes together with their derivatives
up to the second and including zero values, except for one that ensures the implementation
of the specified conditions:
having a bypass nodes together with their derivatives
up to the second and including zero values, except for one that ensures the implementation
of the specified conditions: ![]() .
.
![]() ,
, ![]() (2)
(2)
As the transition functions, you
can use algebraic polynomials, although not ruled out the possibility of using
other functions.
If we consider polynomials of the
same degree, then ![]() will have the form
will have the form
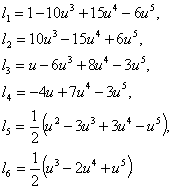 (3)
(3)
In differentiating (1) to ![]() have
have
![]() (6)
(6)
![]() (5)
(5)
Equations (1) to (4) and (5) ![]() give
give ![]() ,
, ![]() ,
, ![]() . At
. At ![]() have
have ![]() ,
, ![]() ,
, ![]() .
.
Equation (1) can be written in
powers ![]()
![]() (6)
(6)
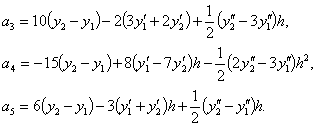 (7)
(7)
Transition functions can be used to
construct the arc II order of smoothness of I commit. In this case, in Equation (1) member ![]() will be omitted, and the coefficients
will be omitted, and the coefficients ![]() you can take other
you can take other
![]() (8)
(8)
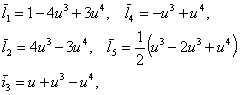 (9)
(9)
The meaning ![]() a first bypass point is given from the additional
conditions (e.g., convexity input), then the equation of the second derivative
of the arc (8) is determined
a first bypass point is given from the additional
conditions (e.g., convexity input), then the equation of the second derivative
of the arc (8) is determined ![]() and equation (8) is used for the next arc.
and equation (8) is used for the next arc.
If the paint (8) in powers ![]() obtain
obtain
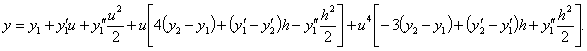 (10)
(10)
To bypass the zero fixation
![]() , (11)
, (11)
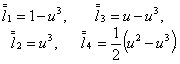 (12)
(12)
Value ![]() and
and ![]() selecting only the first point bypass, the remaining
points are calculated sequentially.
selecting only the first point bypass, the remaining
points are calculated sequentially.
After the transformation (11), we
have
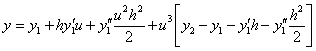 . (13)
. (13)
To bypass the I-order smoothness
![]() (14)
(14)
![]() (15)
(15)
or powers ![]() (16)
(16)
Arc bypass I order smoothness zero
fixation described by the equation
![]() , (17)
, (17)
where ![]()
![]()
![]() (18)
(18)
![]() selected at the first point, and the rest is
calculated by the equation
selected at the first point, and the rest is
calculated by the equation
![]() ,
, ![]() (19)
(19)
Here is a set of trigonometric
polynomials as transition functions to bypass II order smoothness and fixing
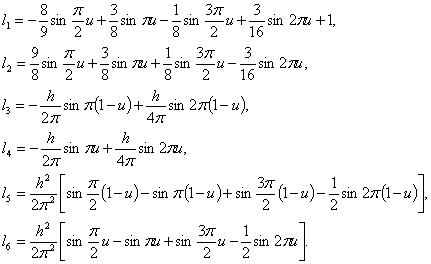 (20)
(20)
You can create a similar set of
contours for a smooth and fixation, but with the implementation of the
necessary conditions preassigned turbine blade design.