Engineering science / 8. Processing of materials in mechanical engineering.

Postgraduate Konkina V.V. , Candidate of Engineering Sciences Solovjev D.S., Eryshova A.S.
Tambov State Technical University, Russia

OPTIMIZATION OF PROCESS CONTROL OF REVERSE MODE ELECTROPLATING IN MULTI ANODE BATH

One of the main objectives of automation of galvanic processes is obtaining uniform plating. According to the authors, an implementation of reverse mode in multi anode bath is the most promising method of reducing the nonuniformity of electrolytic plating. Nevertheless, the implementation would be ineffective without developing algorithms of the process control for such method.

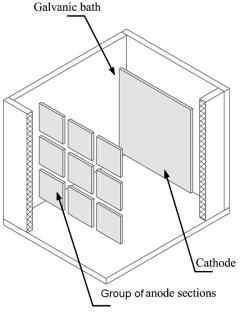
In the proposed process, a monolithic anode (fig. 1a) divides into a group of equal sized sections with density MxN, which are placed in one plane at equal distance from each other, as well as from walls of bath and in front of cathode product (fig. 1b – a group of 3x3 anode sections). Such group of sections connect to a programmable power supply via a device which can turn off the required anode sections. This connection enables to establish either "direct" or "reverse" mode of current reversal in order to reduce the nonuniformity of electrolytic plating due to the fact that during the course of "direct" and "reverse" current the speed of cathode metal coating dissolution is faster on surfaces that nearer to the anode sections, rather than on those which are far from them.

The mathematical formulation of the problem of the optimal process control is as follows: find arrays of active anode sections for "direct" and "reverse" mode of electroplating process reversal, as well as the duration , of such phases, which minimize the criterion of nonuniformity of the thickness of the coating on the cathode surface S_k:

, (1)

the following restrictions must be carried out:

, (2)

(3)

where – the given thickness of plating; – the minimum thickness of the plating; – the maximum thickness of the plating; Т – the duration of electroplating process; Т^max – the maximum length of electroplating process; x, y, z – coordinates of a point in the space of the plating bath; υ – a number of phases of switching on the "direct" and "reverse" current.

(a)

(b)

Fig. 1. Structural scheme of galvanic bath with monolithic anode (a) and a group of 3х3 anode sections (b)

In the work [1] a mathematical model, containing Faraday's law, Ohm’s law in differential form, as well as the Laplace’s differential equation in partial derivatives, is being proposed for the above-described process.

The objective of finding the optimal process control of proposed method represents a partially integer objective of a binary nonlinear programming. On the assumption of the well-known drawbacks of the existing approaches to the solution of integer programming problems (branch and bound methods, combinatorial problems), the authors have chosen the method of an exhaustive search to find the optimal configuration for a group of active anode sections in "direct" or "reverse" mode of current reversal, where pattern-search method, by Hooke-Jeeves, has been used to find durations of duty cycles [2].

After specifying the dimensionality of the group of anode sections and its configuration, as well as the geometry of cathode product, restrictions on the values of the minimum specified thickness of the coating (2) and process duration (3) two cycles begin: cycles on the formation of arrays of active anode sections in "direct" or "reverse" mode of electroplating process. The number of iterations in each cycle is 2^M∙N times, which is explained by the possibility of taking only binary values for the array elements. At the same time the selection of durations τ^dir and τ^rev is carried out according to the selected algorithm. After calculating all the values of criteria of non-uniformity, optimal process control actions are selected to ensure its minimum (1).

References:

1. Konkina V.V., Solovjev D.S. Matematicheskaya postanovka zadachi optimalnogo upravleniya galvanicheskim protsessom v reversivnom rezhime dlya mnogoanodnoy vannyi [Mathematical formulation of the problem of optimal control of electroplating process in reverse mode for multianode bath] // Teoreticheskie i prakticheskie aspektyi tehnicheskih nauk: sb. statey mezhdunar. nauch.-prakt. konf. – Ufa: «Aeterna». 2014. pp. 41 – 43.

2. Konkina V.V., Solovjev D.S. Mathematical modelling of electroplating in reverse mode for the multianode bath. ISJ Theoretical & Applied Science. 2015. vol. 03, no 23. pp. 59 – 62.