Алин Ж.Д.

Казахский Национальный Технический

университет имени К. Сатпаева.

Республика Казахстан, г. Алматы.

Критерий существования гладкого и сильного решений задачи Трикоми для уравнения Геллерстедта

Со времен постановки и исследования краевой задачи Дирихле для уравнения Лапласа теория краевых задач для различных типов линейных дифференциальных уравнений в частных производных занимает одно из центральных мест в анализе, прежде всего благодаря своим приложениям, охватывающим всю математическую физику, а также многие области механики и инженерного дела.

Проблемы теории краевых задач стимулировали появление новых направлений в функциональном анализе, в теории интегральных уравнений и в теории функций, а применение теории интегральных уравнений, теории интегральных преобразований функции, результатов и методов функционального анализа приводило к решению давно стоявших задач теории краевых задач.

Важным направлением исследования в теории краевых задач является постановка и исследование новых корректных краевых задач для линейных уравнений гиперболического и смешанного типов.

Постановка и исследование корректной краевой задачи для уравнения смешанного типа впервые был получен итальянским математиком Ф. Трикоми. Франкль В.И. обнаружил важные приложения задачи Трикоми в газовой динамике. Бицадзе А.В. сформулировал принцип экстремума для задачи Трикоми. Спектральные вопросы для теории уравнении смешанного типа рассматривались в работах Кальменова Т.Ш., Моисеева Е.И.

Основные методы исследования задачи Трикоми подразделяются на следующие два вида.

Первым методом исследования, предложенный Ф. Трикоми, задача Трикоми для широкого класса уравнении смешанного типа сводится к эквивалентной задаче разрешимости и единственности решения одновременно сингулярного уравнения типа Карлемана.

Этим методом исследования задачи Трикоми рассматривалась в работах Бизадзе А.В., Нахушева А.М., Волкодавов В.Ф., Репин О.А., Бабенко К.И., Салахитдинова М.С., Солдатова А.П. и других.

Вторым методом исследования задачи Трикоми является так называемый метод «а», «b», «c». Этот метод предложен американским математиком Проттером М.Х. Основная идея этого метода состоит в том. Что для гладких решений при некоторых ограничениях на поведение границы эллиптической границы области получаются априорные оценки решения задачи Трикоми через правую часть уравнения. Далее, применяя фундаментальную теорему функционального анализа Хана-Банаха из функционального анализа о продолжении функционала из подпространства на все гильбертовое пространство с сохранением нормы получается существование слабого решения задачи Трикоми.

Этим методом задача Трикоми исследовалась в работах Catrheen S. Morawetz, Коврижкина В. и других.

В работах P.D. Lax, R.S. Phillips и Сорокиной Н.Г. применяются специальные методы усреднения функции и доказывается, что слабое решение задачи Трикоми для уравнении Чаплыгина на самом деле являются сильным. В работе задача Трикоми для уравнения Геллерстедта исследуется при помощи применения операционного исчисления. В зависимости от проведения границы эллиптической части смешанной области получены критерии существования гладкого и разрывных решений задачи Трикоми.

Пусть - конечная область, ограниченная при кривой Ляпунова

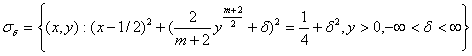
а при - характеристиками

уравнения Геллерстедта

(1)

где

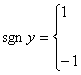при при

В случае и в работах Ф.Трикоми и А.И. Бицадзе для нормального контура

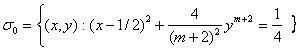
Хорошо изучена следующая задача.

Задача Трикоми. Найти решение уравнения (1), удовлетворяющее краевому условию (2)

При непрерывном условии склеивания решения на линии изменения типа : . Введем следующий класс функции гладких решении задачи Трикоми для уравнения (1)

Определение 1.1. Решение задачи Трикоми называется гладким, если оно принадлежит классу .

Отметим, что в случае нормального контура решение задачи Трикоми для гладких правых частей в уравнении (1) может не принадлежать классу .

Задача Трикоми исследуется для всех контуров . По числу определим следующее число

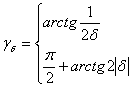при при

И сформулируем основные результаты.

Теорема 1.1. Для всех правых частей в уравнении (1) из класса решение задачи Трикоми будет гладким (то есть ) тогда и только тогда, когда

(3)

Теорема 1.2. Для всех правых частей в уравнении (1) из класса , где решение задачи Трикоми при принадлежит классу тогда и только тогда, когда

При и и решение задачи Трикоми может быть разрывным в области и причем решение обращается в бесконечность в точке порядка

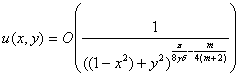
Для задачи Трикоми в уравнении Геллерстедта в зависимости от поведения границы эллиптической части области получен критерий существования гладкого решения. В частности, для некоторых контуров в случае сильного вырождения (т.е. m>2) существует разрывные решения даже для гладких правых частей.