Современные информационные технологии/Вычислительная техника и программирование

Мясищев А.А.

Хмельницкий национальный университет, Украина

Анализ целесообразности использования многоядерных процессоров для решения параллельных задач на примере матричного умножения.

Постановка задачи

Матрицы и матричные операции широко используются при математическом моделировании самых разнообразных процессов, явлений и систем. Матричные вычисления составляют основу многих научных и инженерных расчетов. Они часто связаны с решением систем уравнений в частных производных (задачи расчета на прочность, переноса тепла и т.д.).

С учетом значимости эффективного выполнения матричных расчетов многие стандартные библиотеки программ содержат процедуры для различных матричных операций. Объем программного обеспечения для обработки матриц постоянно увеличивается – разрабатываются новые экономные структуры хранения для матриц специального типа (треугольных, ленточных, разреженных и т.п.), создаются различные высокоэффективные машинно-зависимые реализации алгоритмов, проводятся теоретические исследования для поиска более быстрых методов матричных вычислений.

Являясь вычислительно трудоемкими, матричные вычисления представляют собой классическую область применения параллельных вычислений. С одной стороны, использование высокопроизводительных многопроцессорных систем позволяет существенно повысить сложность решаемых задач. С другой стороны, в силу своей достаточно простой формулировки матричные операции предоставляют прекрасную возможность для демонстрации многих приемов и методов параллельного программирования.

В данной работе рассматривается еще один способ параллельных вычислений – задача перемножения матриц, но для четырехядерных процессоров с помощью технологии MPI. Здесь будем полагать, что рассматриваемые матрицы являются плотными, то есть число нулевых элементов в них незначительно по сравнению с общим количеством элементов матриц.

Для удобства отслеживания производительности компьютера на конкретном приложении будем фиксировать производительность систем в Мегафлопсах (1 Mflops - миллион операций с плавающей точкой за одну секунду). Для оценки этой величины будем измерять время выполнения фиксированного числа реальных операций, которые выполняются системой.

Разделив число операций на время, умноженное на 1000000, получим производительность системы в Мегафлопсах

В качестве вычислительной системы рассмотрим две системы, соединенные с помощью сети Ethernet со скоростью 1 Гбит/с, построенные на базе четырехядерных процессорах CORE 2 QUAD PENTIUM Q6600 2.4GHZ. В качестве программного обеспечения будем использовать кластер PelicanHPC GNU/Linux v.1.7.2, работающего как "Live CD". Адреса входящих в систему компьютеров имели значения 10.11.12.1 и 10.11.12.2. Управление библиотеками MPI выполнялось с помощью файла /home/user/tmp/bhosts, в котором описывались входящие компьютеры в систему и число используемых процессоров в каждом из них. Например, для двух компьютеров с задействованными 4-я ядрами в каждом из них файл имел вид

10.11.12.2 cpu=4

10.11.12.1 cpu=4

В этом случае система рассматривалась как восьми процессорная. Для преобразования ее в четырехпроцессорную, достаточно изменить файл на

10.11.12.2 cpu=2

10.11.12.1 cpu=2

и применить команду

lamboot /home/user/tmp/bhosts

Будем считать, что файл /home/user/tmp/bhosts определяет архитектуру параллельной системы.

Классическая последовательность операций при перемножении матриц

Рассмотрим последовательность действий выполняемых при перемножении квадратной матрицы. В качестве примера для последующего обобщения зависимостей для вычисления членов результирующей матрицы рассмотрим произвольные матрицы размерностью N=4.

* =

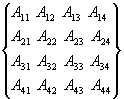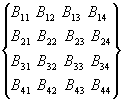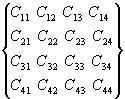
Рассмотрим построчное вычисление членов матрицы C . Это важно для реализации параллельного алгоритма вычисления произведения.

Определение членов матрицы C для первой строки определяется следующим образом:

Аналогично для второй строки:

Окончательно любой элемент матрицы C можно представить так:

, здесь I – номер строки.

Фрагмент программы на Фортране для построчного вычисления произведения может выглядеть так:

do 2 i=1,n

do 2 j=1,n

c(i,j)=0.

do 3 k=1,n

3 c(i,j)=c(i,j)+a(i,k)*b(k,j)

2 continue

Учитывая, что компилятор Фортрана располагает двумерные массивы в памяти по столбцам этот фрагмент можно модернизировать так:

do 2 i=1,n

do m=1,n

aa(m)=a(i,m)

end do

do 2 j=1,n

c(i,j)=0.

do 3 k=1,n

3 c(i,j)=c(i,j)+aa(k)*b(k,j)

2 continue

Такая модернизация более экономно использует кэш память и существенно повышает производительность расчетов при использовании ключа компилятора –O3.

Программа перемножения матриц для одного ядра процессора

Программа выполняет перемножение матриц порядка n=2000. Определение элементов матрицы производится последовательно по строкам.

program lab7_1

include 'mpif.h'

parameter (n=2000)

integer ierr,rank,size,i,j,k,ii

real*8 :: a(n,n), b(n,n), c(n,n), aa(n)

real*8 :: r1,mf,op

double precision time1, time, time2

integer status(MPI_STATUS_SIZE)

call MPI_INIT(ierr)

call MPI_COMM_SIZE(MPI_COMM_WORLD, size, ierr)

call MPI_COMM_RANK(MPI_COMM_WORLD, rank, ierr)

c initial data

do 10 i=1,n

do 10 j=1,n

a(i,j)=1.0d0*i*j

b(i,j)=1.0d0/a(i,j)

c(i,j)=0.d0

10 continue

c First part of the matrix

if(rank.eq.0) then

time1 = MPI_Wtime()

do 2 i=1,n

do m=1,n

aa(m)=a(i,m)

end do

do 2 j=1,n

c(i,j)=0.d0

do 3 k=1,n

3 c(i,j)=c(i,j)+aa(k)*b(k,j)

2 continue

time2 = MPI_Wtime()

time = time2-time1

do 7 i=1,8

7 print 8,c(i,1),c(i,2),c(i,3),c(i,4),c(i,5),c(i,6),c(i,7),

&c(n-i,n/2+i)

8 format(1x,8f9.3)

r1=0.d0

do ii=1,n

r1=r1+c(ii,ii)

end do

op=(2.0*n-1)*n*n

mf=op/(time*1000000.0)

print *,' diagonal=',r1

print *,' process=',rank,' time = ',time, 'mf=',mf

end if

call MPI_FINALIZE(ierr)

end

Программа перемножения матриц для четырехядерного процессора

Программа выполняет перемножение матриц порядка n=2000. Определение элементов матрицы производится построчно. Для нулевого процесса идет расчет матрицы с 1-й строки по n/4. Для первого процесса производится расчет с n/4+1 строки до n/2 -й. Для второго процесса производится расчет с n/2+1 строки до 3*n/4. Для третьего процесса производится расчет с 3*n/4+1 строки до n. Пересылка данных выполняется с помощью дополнительного массива cc(n,n). После пересылки к нулевым членам массива c(i,j) добавляются рассчитанные в 1-м 2-м и 3-м ядрах процессора члены массива cc(i,j). Для повышения производительности выполняется подстановка линейного массива, как и в однопроцессорной программе

program lab7_2

include 'mpif.h'

parameter (n=2000)

integer ierr,rank,size,i,j,k,ii

real*8 :: a(n,n), b(n,n), c(n,n), cc(n,n),aa(n)

&,aa1(n),aa2(n),aa3(n)

real*8 :: r1,op,mf

double precision time1, time, time2

integer status(MPI_STATUS_SIZE)

call MPI_INIT(ierr)

call MPI_COMM_SIZE(MPI_COMM_WORLD, size, ierr)

call MPI_COMM_RANK(MPI_COMM_WORLD, rank, ierr)

c initial data

do 10 i=1,n

do 10 j=1,n

a(i,j)=1.0d0*i*j

b(i,j)=1.0d0/a(i,j)

c(i,j)=0.d0

10 continue

c First part of the matrix

if(rank.eq.0) then

time1 = MPI_Wtime()

do 2 i=1,n/4

do m=1,n

aa(m)=a(i,m)

end do

do 2 j=1,n

c(i,j)=0.d0

do 3 k=1,n

3 c(i,j)=c(i,j)+aa(k)*b(k,j)

2 continue

call MPI_RECV(cc(1,1),n*n,MPI_DOUBLE_PRECISION,1,5,

&MPI_COMM_WORLD,status,ierr)

do 11 i=n/4+1,n/2

do 11 j=1,n

11 c(i,j)=cc(i,j)

call MPI_RECV(cc(1,1),n*n,MPI_DOUBLE_PRECISION,2,5,

&MPI_COMM_WORLD,status,ierr)

do 22 i=n/2+1,3*n/4

do 22 j=1,n

22 c(i,j)=cc(i,j)

call MPI_RECV(cc(1,1),n*n,MPI_DOUBLE_PRECISION,3,5,

&MPI_COMM_WORLD,status,ierr)

do 33 i=3*n/4+1,n

do 33 j=1,n

33 c(i,j)=cc(i,j)

time2 = MPI_Wtime()

do 7 i=1,8

7 print 8,c(i,1),c(i,2),c(i,3),c(i,4),c(i,5),c(i,6),c(i,7),

& c(n-i,n/2+i)

8 format(1x,8f9.3)

time=time2-time1

op=(2.0*n-1)*n*n

mf=op/(time*1000000.0)

print *,' process=',rank,' time=',time,'mf=',mf

r1=0.0d0

do ii=1,n

r1=r1+c(ii,ii)

end do

print *,' diagonal=',r1

end if

c Second part of the matrix

if(rank.eq.1) then

do 4 i=n/4+1,n/2

do m=1,n

aa1(m)=a(i,m)

end do

do 4 j=1,n

c(i,j)=0.d0

do 5 k=1,n

5 c(i,j)=c(i,j)+aa1(k)*b(k,j)

4 continue

call MPI_SEND(c(1,1),n*n,MPI_DOUBLE_PRECISION,0,5,

&MPI_COMM_WORLD,ierr)

end if

c 3-part of the matrix

if(rank.eq.2) then

do 41 i=n/2+1,3*n/4

do m=1,n

aa2(m)=a(i,m)

end do

do 41 j=1,n

c(i,j)=0.d0

do 51 k=1,n

51 c(i,j)=c(i,j)+aa2(k)*b(k,j)

41 continue

call MPI_SEND(c(1,1),n*n,MPI_DOUBLE_PRECISION,0,5,

&MPI_COMM_WORLD,ierr)

end if

c 4-part of the matrix

if(rank.eq.3) then

do 43 i=3*n/4+1,n

do m=1,n

aa3(m)=a(i,m)

end do

do 43 j=1,n

c(i,j)=0.d0

do 53 k=1,n

53 c(i,j)=c(i,j)+aa3(k)*b(k,j)

43 continue

call MPI_SEND(c(1,1),n*n,MPI_DOUBLE_PRECISION,0,5,

&MPI_COMM_WORLD,ierr)

end if

call MPI_FINALIZE(ierr)

end

В представленных выше программах используются числа двойной точности.

Результаты расчетов по представленным выше программам.

1. Двойная точность

В таблице 1 показаны результаты по затратам времени в секундах (числитель) и производительности в Мегафлопсах (знаменатель) для расчета произведений квадратных матриц порядков 500х500, 1000х1000, 2000х2000, 3000x3000 представленными выше программами с использованием 4-х ядер одного компьютера системы. Расчет велся для чисел двойной точности. Файл /home/user/tmp/bhosts имел вид:

10.11.12.1 cpu=4

10.11.12.2 cpu=4

Компиляция и выполнение программ выполнялись командами:

mpi77 prog.f -o prog

mpirun -np 4 prog (для работы 4-х ядер)

Ключ оптимизации –O3 при компиляции не использовался.

Таблица 1

Размер матриц	Одно ядро	Два ядра	Ускорение	Четыре ядра	Ускорение
500	0.715/349	0.363/688	1.97	0.195/1279	3.67
1000	5.88/340	2.98/671	1.97	1.67/1199	3.52
2000	46.31/345	23.44/682	1.98	12.86/1244	3.60
3000	157.71/342	79.38/680	1.99	42.87/1260	3.68

Из таблицы видно, что с увеличением числа ядер практически пропорционально увеличивается ускорение. Поэтому на первый взгляд использование многоядерных процессоров весьма эффективно.

Выполним компиляцию этих же программ, но с ключом –O3:

mpi77 -O3 prog.f -o prog

Затем запустим их:

mpirun -np 4 prog (для работы 4-х ядер)

Результаты эксперимента представлены в таблице 2.

Таблица 2

Размер матриц	Одно ядро	Два ядра	Ускорение	Четыре ядра	Ускорение
500	0.163/1534	0.088/2855	1.85	0.072/3472	2.26
1000	1.66/1199	1.32/1515	1.27	1.58/1269	1.05
2000	13.30/1202	11.72/1365	1.14	12.34/1296	1.08
3000	44.41/1216	39.14/1379	1.13	41.04/1316	1.08

Из таблицы 2 видно, что производительность на одном ядре по сравнению с предыдущим случаем, увеличилась почти в четыре раза. Однако реальное ускорение наблюдается для размера матриц не превышающей 500 элементов, особенно в случае четырехядерного варианта. Таким образом здесь обнаружена неэффективность затрат на приобретение дорогостоящих многоядерных процессоров для решения задач умножения матриц большого размера. Одноядерные процессоры имеют аналогичную производительность в этом примере.

Рассмотрим архитектуру, описанную в файле /home/user/tmp/bhosts в виде:

10.11.12.1 cpu=2

10.11.12.2 cpu=2

В этом случае имеем параллельную вычислительную систему, состоящую из двух компьютеров, соединенных сетью Gigabit Ethernet в каждом из которых установлен двуядерный процессор. Результаты расчетов по представленным выше программам показаны в таблице 3.

Таблица 3

Размер матриц	Одно ядро	Два ядра на одном компьютере	Ускорение	Два компьютера с двуядерными процессорами	Ускорение
500	0.163/1534	0.088/2855	1.85	0.099/2523	1.65
1000	1.66/1199	1.32/1515	1.27	0.85/2352	1.98
2000	13.30/1202	11.72/1365	1.14	6.64/2407	2.00
3000	44.41/1216	39.14/1379	1.13	21.90/2465	2.02

Из таблицы 3 видно, что ускорение для двух ядер на одном компьютере не изменилось, но почти в два раза возросло ускорение для всей системы. Таким образом, система с распределенной памятью дает явный выигрыш в ускорении по сравнению с многоядерной системой в одном процессоре. Следовательно, для рассмотренных программ реального ускорения можно достичь в случае использования систем с распределенной памятью. Окончательное подтверждение этому дает вычислительный эксперимент с архитектурой:

10.11.12.1 cpu=1

10.11.12.2 cpu=1

В этом случае моделируется параллельная система на базе двух компьютеров, в которых используется процессор Q6600 с одним работающим ядром. В таблице 4 представлены результаты расчетов.

Таблица 4

Размер матриц	Одно ядро	Два компьютера по одному ядру	Ускорение
500	0.163/1534	0.11/2360	1.48
1000	1.66/1199	0.93/2150	1.78
2000	13.30/1202	7.40/2162	1.80
3000	44.41/1216	24.08/2243	1.84

Увеличение ускорения с увеличением размера матриц связано с уменьшением доли времени на пересылку данных между компьютерами, по сравнению со временем, затрачиваемым на вычисление. Сравнивая результаты вычислений по таблицам 2 и 4 можно видеть, что одна четырехядерная система выполняет перемножение матриц размерностью 3000 элементов за 41.04 секунды, а соединенные две системы в каждой из которых задействовано только по одному ядру выполняет те же вычисления за 24.08 секунды. Таким образом, в настоящее время предпочтение для решения задач такого типа нужно отдать распределенным системам.

2. Одинарная точность

Рассмотрим решение этой задачи но при условии, что расчеты выполняются с одинарной точностью. Для этого в программах оператор real*8 необходимо заменить real, а значение переменных типа c(i,j)=0.d0 поменять на c(i,j)=0.0. В таблице 5 представлены результаты расчета для архитектуры

10.11.12.1 cpu=4

10.11.12.2 cpu=4

А в таблице 6 для архитектуры

10.11.12.1 cpu=2

10.11.12.2 cpu=2

Таблица 5

Размер матриц	Одно ядро	Два ядра на одном компьютере	Ускорение	Четыре ядра на одном компьютере	Ускорение
500	0.16/1552	0.084/2982	1.92	0.047/5255	3.39
1000	1.32/1520	0.68/2951	1.94	0.72/2788	1.83
2000	11.23/1425	6.21/2575	1.81	6.29/2542	1.78
3000	37.77/1430	21.96/1379	1.72	20.95/2577	1.72

Таблица 6

Размер матриц	Одно ядро	Два ядра на одном компьютере	Ускорение	Два компьютера с двуядерными процессорами	Ускорение
500	0.16/1552	0.084/2982	1.92	0.067/3746	2.41
1000	1.32/1520	0.68/2951	1.94	0.44/4558	3.00
2000	11.23/1425	6.21/2575	1.81	3.51/4555	3.20
3000	37.77/1430	21.96/1379	1.72	11.52/4685	3.28

Из таблицы 5 видно, что для двуядерного варианта достигнуто практически максимальное ускорение, величина которого падает с увеличением размера матрицы. Но для четырех ядер ускорение только для матрицы с размером 500 достигло почти максимального ускорения, но затем стало постепенно падать с увеличением размера матриц. Однако, общее ускорение одной системы с четырьмя ядрами для чисел с одинарной точностью выше, чем для чисел с двойной точностью (см. таблица 2 и таблица 5).

Сопоставление таблиц 6 и 3 показывает, что для одинарной точности расчет на двух компьютерах с двуядерным процессором дает почти 4-х кратное ускорение (3.28), а в случае двойной точности только двукратное (2.02).

Представленный анализ позволяет сделать заключение, что многоядерные системы эффективны лишь для решения тех задач, которые не требуют использования больших объемов оперативной памяти. Т.е. достаточно объема кэш памяти первого уровня. Поскольку у процессора Q6600 размер кэш памяти первого уровня составляет всего 64 килобайт, то это и приводит к такому низкому результату при выполнении параллельных вычислений.

Для примера в таблице 7 представлен результат решения задачи умножения матрицы с числами двойной точности на параллельной системе из двух компьютеров, в которых установлены процессоры AMD Atlon 64x2 4000+. Архитектура системы представлена файлом /home/user/tmp/bhosts в виде:

10.11.12.1 cpu=2

10.11.12.2 cpu=2

Таблица 7

Размер матриц	Одно ядро	Два ядра на одном компьютере	Ускорение	Два компьютера с двуядерными процессорами	Ускорение
500	0.48/519	0.32/790	1.50	0.21/1215	2.29
1000	3.72/537	2.37/842	1.57	1.34/1489	2.78
2000	29.50/542	18.6/861	1.59	9.98/1603	2.96
3000	98.7/547	61.6/876	1.60	32.48/1663	3.04

Сравнение результатов расчетов в таблицах 3 и 7 позволяет сделать вывод, что процессор фирмы AMD более эффективен для использования в многоядерных параллельных системах, так как он выдает ускорение для всей системы 3.04 по сравнению 2.02 для системы с процессором Q6600. Хотя быстродействие процессора Atlon 64x2 4000+ на одно ядро более чем в два раза ниже Q6600. Такое значение ускорения логично связано с объемом кэш памяти процессора Atlon 64x2 4000+, которая равна 128 килобайт. Таким образом, чем выше объем кэш памяти первого уровня многоядерного процессора, тем более он эффективен для решения параллельных задач, требующих использования больших объемов памяти.

Модификация программы умножения матриц

В настоящее время развитие микропроцессоров идет в направлении увеличения количества ядер на одном кристалле. Судя по заявлениям производителей процессоров, эта тенденция будет сохраняться и далее. В связи с этим рассмотрим простой пример такой модификации программы перемножения матриц, которая даст возможность повысить ускорение расчетов за счет более эффективного использования кэш памяти.

Рассмотрим процедуру умножения матриц на примере матриц с 4-я элементами, которую впоследствии усложним в программе для матриц с любым числом элементов.

* =

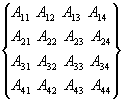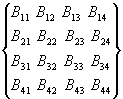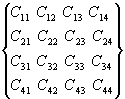
Выделим из матриц A и B четыре матрицы

, , , ,

, , ,

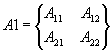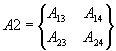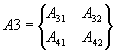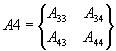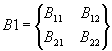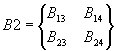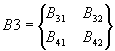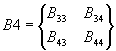
Выполним умножение этих «подматриц» матриц A и B:

,

, ,

, .

,

, ,

, .

,

, ,

, .

,

, ,

, .

,

, ,

, .

,

, ,

, .

,

, ,

, .

,

, ,

, .

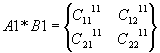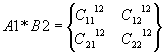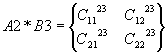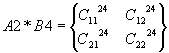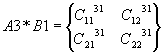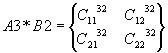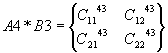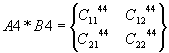Элементы матрицы C с учетом перемножения «подматриц» можно получить в следующем виде:

,

,

,

,

,

,

,,

,

,

,

,

,

,

,

,

Аналогичные зависимости можно записать для перемножения двух матриц с любым числом элементов, но в случае, если исходные матрицы делятся на четыре части. Из простого примера перемножения матриц при их разбиении видно, что модифицированная программа резко усложняется и для ее написания необходимы затраты дополнительного времени и более высокая квалификация программиста.

В программе на каждом ядре процессора выполнялось перемножение двух подматриц:

0-е ядро A1*B1, A1*B2;

1-е ядро A2*B3, A2*B4;

2-е ядро A3*B1, A4*B3;

3-е ядро A3*B2, A4*B4;

Затем результат перемножения передавался на 0-й процессор, который выполнял по последним соотношениям определение элементов матрицы C.

Ниже представлена программа для четырех ядер:

program lab7_3

include 'mpif.h'

parameter (n=1000)

parameter (m=500)

integer ierr,rank,size,i,j,k,ii,m1

real*8 a(n,n),a1(m,m),a2(m,m),a3(m,m),a4(m,m),b(n,n),

& b1(m,m),b2(m,m),b3(m,m),b4(m,m),c(n,n),c11(m,m),c12(m,m),

& c23(m,m),c24(m,m),c31(m,m),c43(m,m),aa(m),

& c32(m,m),c44(m,m)

real*8 r1,op,mf

double precision time1, time, time2

integer status(MPI_STATUS_SIZE)

call MPI_INIT(ierr)

call MPI_COMM_SIZE(MPI_COMM_WORLD, size, ierr)

call MPI_COMM_RANK(MPI_COMM_WORLD, rank, ierr)

c initial data

do 10 i=1,m

do 10 j=1,m

a1(i,j)=0.0d0

a2(i,j)=0.0d0

a3(i,j)=0.0d0

a4(i,j)=0.0d0

b1(i,j)=0.0d0

b2(i,j)=0.0d0

b3(i,j)=0.0d0

b4(i,j)=0.0d0

c11(i,j)=0.0d0

c12(i,j)=0.0d0

c23(i,j)=0.0d0

c24(i,j)=0.0d0

c31(i,j)=0.0d0

c32(i,j)=0.0d0

c43(i,j)=0.0d0

c44(i,j)=0.0d0

10 continue

do i=1,m

do j=1,m

a1(i,j)=1.d0*i*j

b1(i,j)=1.d0/a1(i,j)

end do

end do

do i=1,m

do j=1,m

a2(i,j)=1.d0*i*(j+m)

b2(i,j)=1.d0/a2(i,j)

end do

end do

do i=1,m

do j=1,m

a3(i,j)=1.d0*(i+m)*j

b3(i,j)=1.d0/a3(i,j)

end do

end do

do i=1,m

do j=1,m

a4(i,j)=1.d0*(i+m)*(j+m)

b4(i,j)=1.d0/a4(i,j)

end do

end do

c First part of the matrix

if(rank.eq.0) then

time1 = MPI_Wtime()

do 2 i=1,m

do m1=1,m

aa(m1)=a1(i,m1)

end do

do 2 j=1,m

c11(i,j)=0.d0

do 3 k=1,m

3 c11(i,j)=c11(i,j)+aa(k)*b1(k,j)

2 continue

do 4 i=1,m

do m1=1,m

aa(m1)=a1(i,m1)

end do

do 4 j=1,m

c12(i,j)=0.d0

do 5 k=1,m

5 c12(i,j)=c12(i,j)+aa(k)*b2(k,j)

4 continue

c Zbor massivov

call MPI_RECV(c23(1,1),m*m,MPI_DOUBLE_PRECISION,1,5,

&MPI_COMM_WORLD,status,ierr)

call MPI_RECV(c24(1,1),m*m,MPI_DOUBLE_PRECISION,1,5,

&MPI_COMM_WORLD,status,ierr)

call MPI_RECV(c31(1,1),m*m,MPI_DOUBLE_PRECISION,2,5,

&MPI_COMM_WORLD,status,ierr)

call MPI_RECV(c43(1,1),m*m,MPI_DOUBLE_PRECISION,2,5,

&MPI_COMM_WORLD,status,ierr)

call MPI_RECV(c32(1,1),m*m,MPI_DOUBLE_PRECISION,3,5,

&MPI_COMM_WORLD,status,ierr)

call MPI_RECV(c44(1,1),m*m,MPI_DOUBLE_PRECISION,3,5,

&MPI_COMM_WORLD,status,ierr)

do i=1,m

do j=1,m

c(i,j)=c11(i,j)+c23(i,j)

end do

end do

do i=m+1,n

do j=1,m

c(i,j)=c31(i-m,j)+c43(i-m,j)

end do

end do

do i=1,m

do j=m+1,n

c(i,j)=c12(i,j-m)+c24(i,j-m)

end do

end do

do i=m+1,n

do j=m+1,n

c(i,j)=c32(i-m,j-m)+c44(i-m,j-m)

end do

end do

time2 = MPI_Wtime()

do 7 i=1,8

7 print 8,c(i,1),c(i,2),c(i,3),c(i,4)

&, c(i,5),c(i,6),c(i,7),c(n-i,n/2+i)

8 format(1x,8f9.3)

time=time2-time1

op=(2.0*n-1)*n*n

mf=op/(time*1000000.0)

print *,' process=',rank,' time=',time,'mf=',mf

r1=0.0d0

do ii=1,n

r1=r1+c(ii,ii)

end do

print *,' diagonal=',r1

end if

c Second part of the matrix

if(rank.eq.1) then

do 20 i=1,m

do m1=1,m

aa(m1)=a2(i,m1)

end do

do 20 j=1,m

c23(i,j)=0.d0

do 30 k=1,m

30 c23(i,j)=c23(i,j)+aa(k)*b3(k,j)

20 continue

do 21 i=1,m

do m1=1,m

aa(m1)=a2(i,m1)

end do

do 21 j=1,m

c24(i,j)=0.d0

do 31 k=1,m

31 c24(i,j)=c24(i,j)+aa(k)*b4(k,j)

21 continue

call MPI_SEND(c23(1,1),m*m,MPI_DOUBLE_PRECISION,0,5,

&MPI_COMM_WORLD,ierr)

call MPI_SEND(c24(1,1),m*m,MPI_DOUBLE_PRECISION,0,5,

&MPI_COMM_WORLD,ierr)

end if

c 3-part of the matrix

if(rank.eq.2) then

do 22 i=1,m

do m1=1,m

aa(m1)=a3(i,m1)

end do

do 22 j=1,m

c31(i,j)=0.d0

do 32 k=1,m

32 c31(i,j)=c31(i,j)+aa(k)*b1(k,j)

22 continue

do 23 i=1,m

do m1=1,m

aa(m1)=a4(i,m1)

end do

do 23 j=1,m

c43(i,j)=0.d0

do 33 k=1,m

33 c43(i,j)=c43(i,j)+aa(k)*b3(k,j)

23 continue

call MPI_SEND(c31(1,1),m*m,MPI_DOUBLE_PRECISION,0,5,

&MPI_COMM_WORLD,ierr)

call MPI_SEND(c43(1,1),m*m,MPI_DOUBLE_PRECISION,0,5,

&MPI_COMM_WORLD,ierr)

end if

c 4-part of the matrix

if(rank.eq.3) then

do 24 i=1,m

do m1=1,m

aa(m1)=a3(i,m1)

end do

do 24 j=1,m

c32(i,j)=0.d0

do 34 k=1,m

34 c32(i,j)=c32(i,j)+aa(k)*b2(k,j)

24 continue

do 25 i=1,m

do m1=1,m

aa(m1)=a4(i,m1)

end do

do 25 j=1,m

c44(i,j)=0.d0

do 35 k=1,m

35 c44(i,j)=c44(i,j)+aa(k)*b4(k,j)

25 continue

call MPI_SEND(c32(1,1),m*m,MPI_DOUBLE_PRECISION,0,5,

&MPI_COMM_WORLD,ierr)

call MPI_SEND(c44(1,1),m*m,MPI_DOUBLE_PRECISION,0,5,

&MPI_COMM_WORLD,ierr)

end if

call MPI_FINALIZE(ierr)

end

В таблице 8 представлены результаты работы этой программы для архитектуры параллельной системы

10.11.12.1 cpu=4

10.11.12.2 cpu=4

Таблица 8

Размер матриц	Одно ядро	Два ядра	Ускорение	Четыре ядра	Ускорение
500	0.17/1475	0.089/2793	1.89	0.051/4930	3.34
1000	1.33/1506	0.67/2904	1.93	0.53/3774	2.51
2000	13.25/1207	10.48/1526	1.26	12.41/1288	1.07
3000	45.17/1195	39.73/1379	1.13	41.63/1297	1.08

Сравнение результатов расчета по таблицам 8 и 2 позволяют сделать вывод, что ускорение для матриц с количеством элементов 500 и 1000 возросло (3.34 против 2.26 и 2.51 против 1.05). Для матриц с большим количеством элементов ускорение осталось на прежнем уровне. Также замечено, что для матрицы 1000 несколько увеличилось быстродействие для расчета на одном ядре, хотя количество вычислений для модифицированной программы больше. Таким образом, дальнейшее усложнение программы связанное с дроблением матриц должно привести к более эффективному использованию кэш памяти 1-го уровня, и как следствие, увеличению производительности и достижению ускорения, приближающемуся к количеству ядер процессора.

Выводы.

Для параллельного решения задач на примере перемножения матриц с большим количеством элементов (больше 1000), требующие интенсивной работы с оперативной памятью справедливы утверждения:

1. Многоядерные процессоры не позволяют достичь теоретического ускорения, которое равно количеству ядер для большинства программ, написанных для последовательных систем, которые подверглись распараллеливанию.

2. Системы с распределенной памятью (кластеры для параллельных вычислений), несмотря на относительные медленные каналы связи между вычислительными узлами, позволяют для большинства простых программ достичь ускорения, соответствующее количеству процессоров в системе.

3. Для получения максимального эффекта от применения многоядерных процессоров требуется существенно усложнять программы, приспосабливая их для эффективного использования маленькой кэш памяти 1-го уровня. Это может привести к резкому возрастанию затрат на написание прикладных программ и сделать процесс программирования на многоядерных системах неэффективным.

Литература

1. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб: БХВ – Петербург, 2004.-608 с.: ил.

2. Гергель В.П. Теория и практика параллельных вычислений. http://www.intuit.ru/department/calculate/paralltp/ - 2007.

3. PelicanHPC GNU Linux. http://idea.uab.es/mcreel/ParallelKnoppix/