К.т.н. Гнусов Ю.В., Кубрак В.П.

Харьковский национальный университет внутренних дел

Моделирование с помощью

линейных временных рядов

При построении модели, описывающей динамику изменения социально-экономических показателей на основе имеющихся эмпирических данных необходимо осуществление следующей последовательности действий:

1. Определение порядка модели, который делает модель наиболее адекватной для прогнозирования;

2. Оценка параметров модели, т.е. её коэффициентов;

3. Оценка адекватности построенной модели.

Моделирование помощью

Наиболее распространенным способом определения порядка модели является способ, основанный на использовании так называемой частной автокорреляционной функции.

Рассмотрим последовательность авторегрессионных моделей возрастающего порядка:

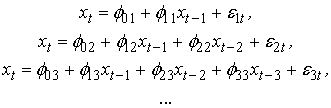
Коэффициенты называют частной автокорреляционной функцией. Так, - частная автокорреляционная функция первого порядка, - частная автокорреляционная функция второго порядка и т.д.

Частная автокорреляционная функция первого порядка показывает, какую часть в величину вносит . Соответственно, показывает вклад в величину и т.д. Следовательно, для модели частная автокорреляционная функция порядка , т.е. , должна быть отлична от нуля, иначе порядок модели можно снизить до . В то же время, частная автокорреляционная функция порядка , т.е. , должна быть равна нулю, иначе порядок модели можно увеличить до .

На практике величины частной автокорреляционной функции заранее не известны и рассчитываются на основе имеющихся реализаций с использованием, например, метода наименьших квадратов. Построенные оценки , и т.д. называются выборочные частные автокорреляционные функции. Для них справедливы следующие утверждения:

сходится к при ;

для всех .

В соответствии с найденным значением , строим модель :

.

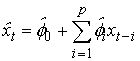В случае адекватности построенной модели ряд остаточных членов , где , является белым шумом. Для проверки гипотез:

где - автокорреляция с лагом ряда применяют так называемую статистику Льюнга-Бокса:

,

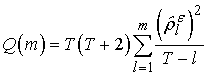которая ассимптотически имеет распределение . Здесь вместо автокорреляций используются выборочные автокорреляции . В качестве параметра можно брать любое целое число, большее порядка модели.

Моделирование с помощью

Определение порядка модели достаточно просто. Оно основано на следующем свойстве автокорреляционной функции модели скользящего среднего, которое мы рассматривали ранее:

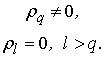
Следовательно, достаточно найти такое значение , для которого выборочная автокорреляция отлична от нуля, а выборочные автокорреляции большего порядка близки к нулю.

Для оценки параметров модели обычно используют метод максимального правдоподобия.

Адекватность построенной модели проверяется тем же способом, что мы рассматривали выше для модели . Однако, в случае модели с параметрами, статистика будет ассимптотически иметь распределение с степенями свободы.

Моделирование с помощью

Моделирование с помощью аналогично выше изложенному.

При определении порядка модели используют выборочную частную автокорреляционную и выборочную автокорреляционную функции. Оценку параметров производят с помощью метода максимального правдоподобия. Статистика Льюнга-Бокса:

,

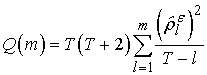используемая для проверки адекватности построенной модели, имеет ассимптотически распределение с степенями свободы.

Остановимся подробнее на особенностях прогнозирования с помощью модели , поскольку нам понадобится этот аспект при расчете величины (Value at Risk). Обозначим через текущий момент времени. Прогноз для момента времени , построенный на основе всей доступной к текущему моменту времени информации обозначим через , т.е. .

Прогноз на один шаг вперед:

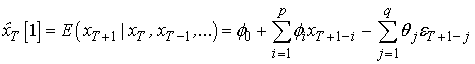
с остатками (ошибками прогнозирования) ,

имеющими вариацию .

Прогноз на шагов вперед:

,

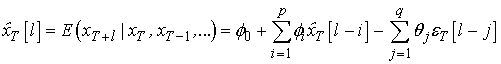где и могут быть получены последовательно.

Из -представления для модели получаем:

,

откуда для ошибки прогнозирования имеем:

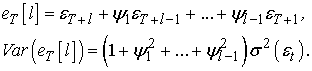
Сезонные модели

Некоторые временные ряды демонстрируют некоторую периодичность в своем поведении. Для того, чтобы провести объективное сравнение таких данных между собой, необходимо прежде всего удалить эту сезонную компоненту. В то же время при прогнозировании поведения таких финансовых временных рядов сезонность является важной компонентой прогноза.

Обычно подразумевается, что финансовый ряд демонстрирует периодичность в своем поведении с периодом , если наблюдается сходство в поведении финансового ряда через каждые временных интервалов. Так, для квартальных данных о прибыли на акцию (квартала), для данных об объемах продаж (месяцев).

Рассмотрим финансовый временной ряд , отражающий, например, квартальные данные о прибыли на акцию. Выборочная автокорреляционная функция, изображенная на рис. 1, демонстрирует высокий уровень корреляции временного ряда.

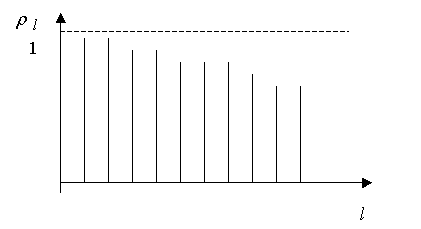
Рис. 1. Выборочная автокорреляционная функция для .

В случае наличия сильной корреляции необходимо рассмотреть ряд разностей первого порядка: .

На рисунке 2 изображена выборочная автокорреляционная функция ряда . Как видно из рисунка, автокорреляция очень сильная при значении лага, кратном четырем. Это и есть эмпирическое подтверждение наличия сезонности с периодом .

Далее рассмотрим следующий ряд разностей, теперь уже четвертого порядка:

.

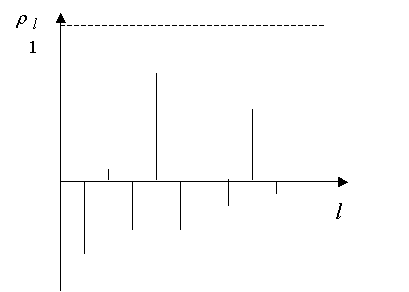
Рис. 2. Выборочная автокорреляционная функция для

В общем случае для временного ряда с сезонной компонентой порядка рассматривается ряд:

или: .

Рисунок 3 показывает выборочную автокорреляционную функцию для . Как видно, выборочные автокорреляции и с лагом 1 и 4 имеют значимое отрицательное значение.

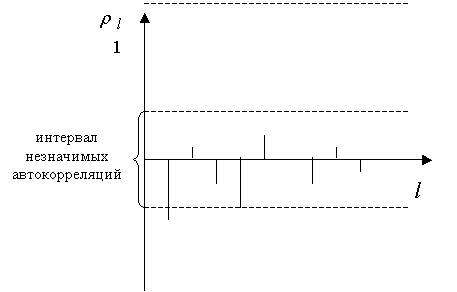
Рис. 3. Выборочная автокорреляционная функция для

Рассмотренные нами линейные модели временных рядов являются важным классом моделей в прогнозировании социально-экономических данных. Однако они не объясняют ряд особенностей поведения временных рядов, таких как кластерность, наличие тяжелых хвостов и асимметрии, долгая память и т.д.