Математика/4. Прикладная математика
К.ф.-м.н. Батыров Б.Е.
Северо-Казахстанский государственный
университет им. М. Козыбаева, Казахстан
Об одном приложении
сверток функций
Изображение – это основной вид представления
информации, которое воспринимается человеком.
Процесс
формирования изображений описывают интегральными уравнениями.
Понятие
изображений полностью укладывается в пространства 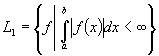 ,
, 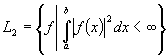 ,
, ![]() . В чисто математическом смысле требование
непрерывности означает, что если есть последовательность функций
. В чисто математическом смысле требование
непрерывности означает, что если есть последовательность функций ![]() , сходящаяся к
, сходящаяся к ![]() , то действие оператора не нарушает сходимости.
, то действие оператора не нарушает сходимости.
Введем
оператор сдвига, который действует на объект ![]() , где
, где ![]() – константа:
– константа: ![]() . Коммутативность
. Коммутативность ![]() с
с ![]() означает, что их
можно менять местами:
означает, что их
можно менять местами:![]() . Это свойство называется пространственной инвариантностью. Наиболее
удобной формой записи изображения является интегральное уравнение Фредгольма I - го рода:
. Это свойство называется пространственной инвариантностью. Наиболее
удобной формой записи изображения является интегральное уравнение Фредгольма I - го рода:
![]() , где
, где ![]() - ядро интегрального
уравнения, описывающего процесс формирования изображения. В физике
- ядро интегрального
уравнения, описывающего процесс формирования изображения. В физике ![]() называется функцией Грина, в оптике – функцией
рассеяния точки, в радиотехнике – импульсной переходной характеристикой, чаще –
аппаратной функцией. В случае коммутации данного интегрального оператора с
оператором сдвига уравнение Фредгольма может быть преобразовано к виду:
называется функцией Грина, в оптике – функцией
рассеяния точки, в радиотехнике – импульсной переходной характеристикой, чаще –
аппаратной функцией. В случае коммутации данного интегрального оператора с
оператором сдвига уравнение Фредгольма может быть преобразовано к виду:
![]() . В этом случае интегральное уравнение сводится к уравнению
типа свертки. Известно, что преобразование Фурье (Фурье-образ) свертки двух
функций равно произведению преобразований Фурье этих функций:
. В этом случае интегральное уравнение сводится к уравнению
типа свертки. Известно, что преобразование Фурье (Фурье-образ) свертки двух
функций равно произведению преобразований Фурье этих функций:
![]() .
.
Для
реконструкции изображения нужно сконструировать обратный оператор, т.е. решить
обратную задачу. Термины прямой и обратной задачи являются строго математическими.
При решении любой обратной задачи возникают три главных вопроса:
1. Существует ли решение
основного интегрального уравнения;
2. Если решение существует, то является ли
оно единственным; 3. Устойчиво
ли решение, т.е. приводят ли малые изменения исходных данных к малым изменениям
решения.
Если решение существует единственное и устойчивое, то
задача называется корректно поставленная. Понятие корректной постановки задач
математической физики было введено Ж.Адамаром и долгое время считалось, что
задача всегда должна удовлетворять этим требованиям. Если задача не
удовлетворяет им, то она называется некорректно поставленная или некорректная.
Задачи реконструкции изображения, как правило, являются некорректно
поставленными, так как не выполняется ни одно из вышеперечисленных условий,
поэтому долгое время считалось, что их решение невозможно. Однако, практика
требовала решение этих задач и в конечном итоге привели к созданию теории
решения некорректных задач.
Рассмотрим
уравнение типа свертки (именно этот тип уравнений используется в томографии):
![]() . (1)
. (1)
Применим преобразование Фурье к двум частям уравнения ![]() : Для нахождения решения возьмем обратное
преобразование Фурье:
: Для нахождения решения возьмем обратное
преобразование Фурье:
![]() .
(2)
.
(2)
Это преобразование возможно при следующих ограничениях
на функции, входящие в состав уравнения: ![]() (интегрируема в квадрате),
(интегрируема в квадрате), ![]() (линейно
интегрируема),
(линейно
интегрируема), ![]() , следовательно,
, следовательно, ![]() при любом
при любом ![]() . Решение, описываемое формулой (2) существует при
. Решение, описываемое формулой (2) существует при ![]() ; если при каких либо ω -
; если при каких либо ω -![]() , то данные частоты не прошли через систему, т.е. в
изображении нет полной информации об объекте. Формально мы не можем
реконструировать объект, следовательно, решение обратной задачи не существует.
В 60-е годы Тихонов А.А. разработал общие принципы решения некорректно
поставленных задач. (Метод реализации Тихонова используется во всех
томографах). Тихонов разработал метод регуляризации решения некорректно
поставленных задач [1]. Решение уравнения (1) имеет вид
, то данные частоты не прошли через систему, т.е. в
изображении нет полной информации об объекте. Формально мы не можем
реконструировать объект, следовательно, решение обратной задачи не существует.
В 60-е годы Тихонов А.А. разработал общие принципы решения некорректно
поставленных задач. (Метод реализации Тихонова используется во всех
томографах). Тихонов разработал метод регуляризации решения некорректно
поставленных задач [1]. Решение уравнения (1) имеет вид
![]() . Функция
. Функция ![]() сглаживает любые
точки выброса и имеет разные виды. Тихонов ввел функцию
сглаживает любые
точки выброса и имеет разные виды. Тихонов ввел функцию
![]() .
.
Оператор ![]() является
регуляризирующим, если функция
является
регуляризирующим, если функция ![]() удовлетворяет
следующим условиям:
удовлетворяет
следующим условиям:
1) ![]() должна быть определена на всей частотной оси в
области -¥<w<¥,
должна быть определена на всей частотной оси в
области -¥<w<¥, ![]() (на всей вещественной оси);
(на всей вещественной оси);
2) Для любого ![]() и
и ![]() ;
;
3) Для любых ![]()
![]() -четная по
-четная по ![]() ;
;
4) Для любых ![]() :
: ![]() при
при ![]() ;
;
5) Если ![]() , то
, то ![]() не убывая, стремится к единице (не может быть колебаний и
осцилляций и функция должна возрастать);
не убывая, стремится к единице (не может быть колебаний и
осцилляций и функция должна возрастать);
6) Для любых ![]() :
: ![]() (иначе не
посчитаем обратное преобразование Фурье);
(иначе не
посчитаем обратное преобразование Фурье);
7) Для любых ![]() при
при ![]() .
.
Функция ![]() , удовлетворяющая этим условиям, называется стабилизирующим
множителем.
, удовлетворяющая этим условиям, называется стабилизирующим
множителем. ![]() можно представить в
виде:
можно представить в
виде:
 ,
,
где ![]() -
неотрицательная четная функция.
-
неотрицательная четная функция.
В качестве
примера функции ![]() можно рассмотреть
функцию
можно рассмотреть
функцию ![]() .
.
Тихонов ввел сглаживающий функционал ![]() , минимизирующий разницу между
, минимизирующий разницу между ![]()
и ![]() :
:  ,
,
где ![]() -
стабилизирующий функционал, который зависит от
-
стабилизирующий функционал, который зависит от ![]() и
и ![]() .
.
Нужно, чтобы изображение от объекта отличалось на
конечную величину. Тихонов доказал, что при выборе a перебором, можно добиться наличия устойчивого решения.
Аналогичную
задачу автор рассматривал для функций из пространства Лизоркина-Трибеля ![]() [2], делал оценки
квазинорм сверток в различных функциональных пространствах для пробных функций [3].
[2], делал оценки
квазинорм сверток в различных функциональных пространствах для пробных функций [3].
Литература:
1.
Тихонов А.Н., Арсенин
В.Я. Методы решения некорректных задач. М. 1979. 283 с.
- Батыров Б.Е. Регуляризация решений уравнения I рода типа свертки в пространствах Лизоркина-Трибеля. I-съезд математиков Казахстана, тезисы докладов. Шымкент. - 1996.- С.99.
- Батыров Б.Е., Буренков В.И. Об оценках сверток в пространствах Никольского-Бесова. // Доклады Российской Академии Наук.-1993.- Т 330.- С. 99 -101.