В. Н. Глушков, Н.В.Могилевская, Е.А.Сизько

Днепропетровский Национальный Университет им.О.Гончара

Вариационный принцип Рэлея-Ритца

с оптимизацией базиса для возбужденных

электронных состояний

Хорошо известно, что многие задачи физики могут быть сведены к проблеме собственных значений самосопряженного оператора Н (гамильтониана в нашем случае), на собственные векторы которого наложены ограничения в виде их ортогональности к некоторому вектору связи. Так, например, для определения первого электронного возбужденного состояния требуется решить задачу (напр.,[1]):

(H – E) |F ñ = 0, (1)

при дополнительном условии

áF₀ |F ñ = 0. (2)

Для приближенного решения задачи (1) хорошо приспособлены схемы, основанные на вариационном принципе Рэлея-Ритца [2]. В соответствии с этим принципом энергия основного состояния, E₀ определяется в результате минимизации частного Рэлея:

E(F) = áF| H |Fñ / áF|Fñ,

E ₀ = E (F₀) = áF₀ | H |F₀ ñ = min áF| H |Fñ / áF|Fñ, áF₀ |F₀ ñ = 1, (3)

FÎM₀

При этом приближенное решение F представляют в виде разложения по конечному числу базисних функций c_р, p = 1,2,…, m₀

|Fñ = S_p C_p |c_pñ, (4)

Через М₀ в (3) обозначено подпространство состояний, натянутое на конечный базис, оптимизированный для основного состояния.

Энергия первого возбужденного состояния Е₁ находится из требования

E ₁ = E (F₁) = áF₁ | H |F₁ ñ = min áF| H |Fñ / áF|Fñ, áF₁ |F₁ ñ = 1, (5)

FÎ {F₀}^{^}

Где минимум берется по всем векторам, принадлежащим ортогональному дополнению {F₀}^{^}, к F₀, т.е. мы имеем дело с условной минимизацией частного Рэлея. Подобным образом определяются более высокие возбужденные состояния. При этом, следует отметить, что в общем случае, базис в (4) для возбужденного состояния должен отличается от базиса, приспособленного для основного состояния, если мы хотим достичь разумной точности расчета возбужденного состояния. На преимущества использования различных базисов для разных состояний указывалось еще в работе [3].

Традиционные методы условной оптимизации (напр.,[4]) плохо приспособлены для решения сложных задач квантовой механики молекул, особенно, если варьировать нелинейные параметры базиса. В данном сообщении мы исследуем эффект оптимизации конечного базиса на точность расчета возбужденных электронных состояний простых молекулярных ионов Н₂⁺ и Н₃²⁺ и используем для этого метод асимптотического проектирования [1, 5, 6], который оказался эффективным инструментом для решения подобного рода задач (см. обзор [1]). Этот метод позволяет свести минимальными вычислительными усилиями условную оптимизацию (5) к безусловной для модифицированного гамильтониана H_mod = H + l|F₀ ñáF₀|, l® ¥. Ключевой идеей подхода является теорема, которая утверждает, что вектор |F₀ ñ становится собственным для модифицированного оператора H_mod при l® ¥. Выполнение ортогональности следует из ортогональности собственных векторов, принадлежащих различным собственным значениям. На практике значение l = 10³ а.е. обеспечивало требуемую точность выполнения условия ортогональности, а именно |áF₀ |F ñ| < 10^-5 (см. подробней [1,5] и ссылки там).

Выбор этих молекулярных систем для исследования обусловлен тем, что для них известны результаты численного решения уравнения Шредингера [7,8] и, таким образом, возможно оценить точность и эффективность используемой методики. Расчеты проводились для основного и первого возбужденного состояний одинаковой симметрии при следующей геометрии ионов: Н₂⁺- межъядерное расстояние R = 2.0 bohr; для линейной конфигурации Н₃²⁺ ядра располагались в точках с координатами: (0.0, 0.0, -2.0), (0.0, 0.0, 0.0) и (0.0, 0.0, +2.0) (все значения в bohr). В качестве базиса были использованы дистрибутивные гауссовые s-функции, параметры экспонент и центровки которых определялись минимизацией энергии данного состояния.

Рис. 1 демонстрирует поведение абсолютной погрешности в энергии | E – E_exact | молекулярного иона Н₂⁺ в зависимости от размерности базиса - m. Кривые “ ¾ “ и “ - - - “ обозначают основное и возбужденное состояния соответственно. При этом для разных состояний использованы различные базисы, оптимизированные для индивидуального состояния, тогда как кривая “ х х х “ соответствует расчетам, где для возбужденного состояния использовался базис, оптимизированный для основного. Как видно из рисунка, даже для малых базисов (напр., m=8), их оптимизация обеспечивает сравнимую погрешность для основного и возбужденного состояний (см. кривые “ ¾ “ и “ - - - “ ). Это означает, что энергия возбуждения DЕ = Е₁ – Е₀ может быть получена с хорошей точностью. Напротив, применение базиса основного состояния для расчета энергии возбужденного состояния ведет к погрешности ~ 10⁵ микрохартри (см. кривая “ ххх “). Эти же тенденции проявляются при изучении трехатомного иона H₃++ . В таблице 1 мы приводим значения полных энергий и погрешность в энергиях вертикального возбуждения для ионов H₂+ и H₃++ . Результаты показывают, что оптимизация базиса в сочетании с методологией асимптотического проектирования позволяет достичь высокой точности в расчетах как энергии возбужденных состояний, так и энергий возбуждения.

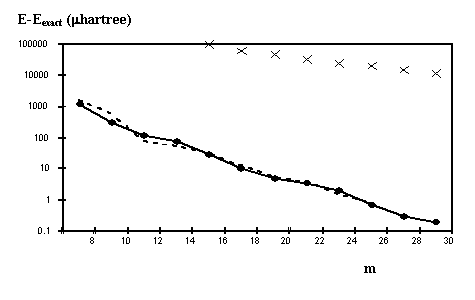
Рис.1 – Ошибка в энергии | E – E_exact | для основного ( ¾ ) и возбужденного ( - - - , х х х) состояний иона H₂⁺ как функция количества базисных функций (m).

Таблица 1: Полные энергии (хартри) и погрешность в энергиях вертикального возбуждения (микрохартри) для H₂+ и H₃++

молекула	базис	E 0	E 1	DE =E1 –Е0	DЕ^exact– DЕ
Н2^+	29s	-0.602 633 99	0.139 135 54	0.741 769 53	0.19
Н3^2+	42s	-1.524 159 62	-1.173 373 83	0.350 785 81	0.21

Литература

1.V. N. Glushkov, N. I. Gidopoulos, and S. Wilson, in Frontiers in Quantum

Systems in Chemistry and Physics, edited by S. Wilson, P. J. Grout, J. Maruani, G. Delgado-Barrio, and P. Piecuch (Springer, Dordrecht, 2008), p. 429.

2. С.Гулд, Вариационные методы в задачах о собственных значениях, Мир: Москва, 1970

3. H.Shull and P.-O. Lowdin, Phys. Rev. Vol. 110, 1466-1467 (1958).

4. P.E.Gill and M.Murray, Numerical methods for constrained optimization, London, Academic Press (1978).

5. V.N.Glushkov, Opt.&Spectrosc. Vol. 93, 15-22 (2002).

6. V.N.Glushkov, J.Math.Chem. Vol. 31, 91-103 (2002).

7. M.M.Madsen and J.M.Peek, Atom. Data. Vol. 2, 171-203 (1971)

8. S.Hackel, D.Heinemann, D.Kolb and B.Fricke, Chem.Phys.Lett. Vol. 206, 91-95 (1993).