Comparative analysis of
approximate methods of solving of differential equations for continuously
variable transmissions
Numerous mechanisms based on a pulsed mechanism with unbalanced elements
are available now [1]. Their dynamics is described by systems of nonlinear
differential equations. In general, precise methods of solution for such
equations do not exist. Therefore, in practice, approximate analytical and
numerical methods must be employed. The main analytical methods employ
successive approximation, a small parameter, or power series expansion. Each
approach has its advantages and disadvantages. Therefore, we need to compare
them in order to select the best method for dynamic study of such kind of
transmissions.
A mathematical model of inertia-pulsed transmission may be based on
Lagrangian equations of the second kind. Using this equation, we obtain a
mathematical model of an inertia-pulsed drive in the form of fifth-order system
of non-linear equations
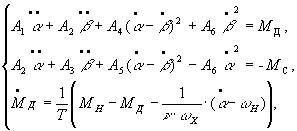(1)
where
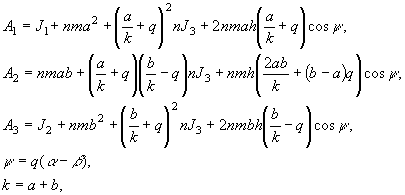
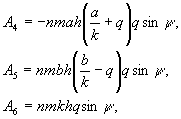
is the reduced drag torque on
the driven shaft of the pulsed mechanism,
are the moments of inertia of
the elements; 
is the total moment of inertia
of the unbalanced elements relative to the geometric center; 
is the total mass of the
unbalanced elements; 
is the distance between the
geometric center and the center of mass of the unbalanced elements; 
are parameters of the pulsed
mechanism.
To
determine the torque 
acting on the driveshaft of the
pulsed mechanism, we use the dynamics characteristic of an asynchronous
electric motor, taking the influence of electromagnetic transient processes
into account
where 
is the rated moment of motor
rotor; 
are the angular velocity in
ideal idling and the rated angular velocity; 
is the electromagnetic time
constant of the motor; 
is the slope of the static
characteristic.
For the
sake of comparison, we solve Eq. (1) by several approximate analytical methods.
METHOD OF SMALL PARAMETER
We rewrite Eq. (1)
in the form
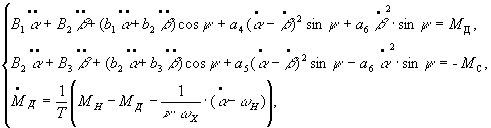(2)
where
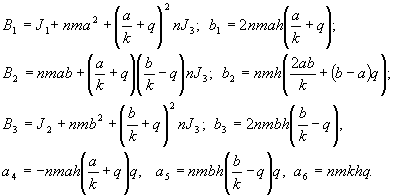
The
coefficients 
contain the moments of inertia 
of the elements of the inertial-pulsed
transmission and are considerably larger than the other coefficients. This
permits the introduction of the small parameter 
in Eq. (2). The system then
takes the form
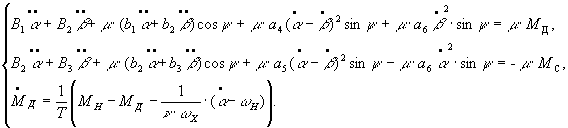(3)
On the
basis of the fundamental principle of the method of small parameter, we look
for the solution in serial form
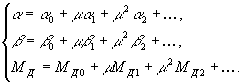(4)
Assuming
that 
, we obtain the generating system
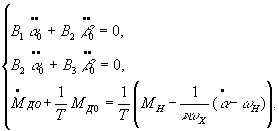
With
the initial conditions 
, the solution of the generating system is
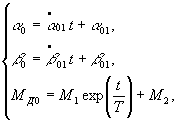
where 
Retaining
only term where 
is of first order and taking
account of the series expansion of the trigonometric functions, we obtain a
system of equations for 
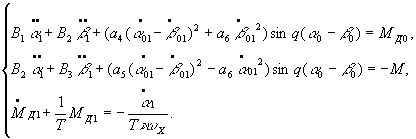(5)
Solving
Eq. (5) with null initial conditions, we obtain expressions for 
and 
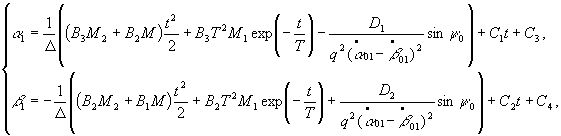
where
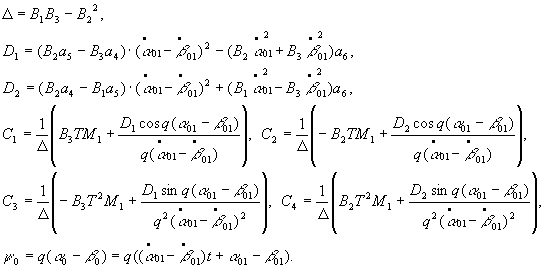
The
solution for 
is
where
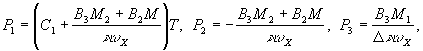
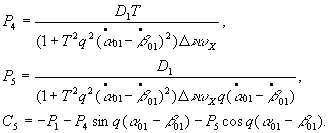
Retraining only the
first two terms in Eq. (4) and assuming that 
, we write the final solution of Eq. (1) by the method of small
parameter
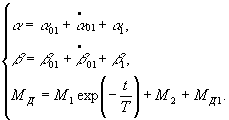
SUCCESSIVE─APPROXIMATION METHOD
The first
approximation is obtained on the basis of the initial conditions
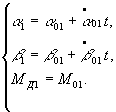
In
particular, taking account of the first approximation and the conditions 
, we obtain the system of differential equations for the second
approximation
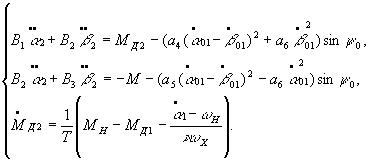(6)
Solving
Eq. (6) with the specified initial conditions, we obtain the second
approximation of Eq. (1). For the motor torque, the second approximation takes
the form 
where 
.
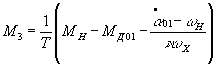The
second approximation for the angle of drive shaft rotation is
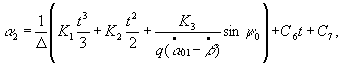
where
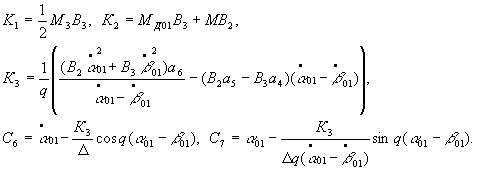
The
second approximation for the angle of driven shaft rotation is
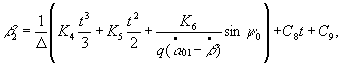
where
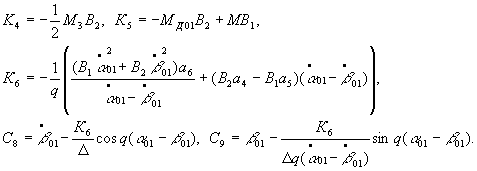
Confining
our attention to the second approximation for 
and 
, we find the third approximation for the motor torque
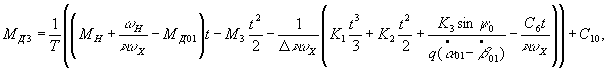where
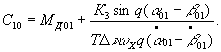
EXPANSION IN POWER SERIES
By this
method, the solution of Eq. (1) is sought in the form
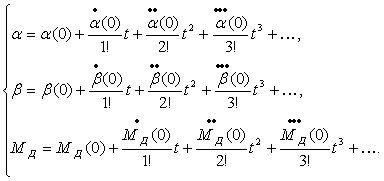(7)
We find
from the initial conditions 
To
determine the second derivatives of 
, and 
, and the first derivative of
the motor torque when 
, we solve Eq. (1) for higher derivatives
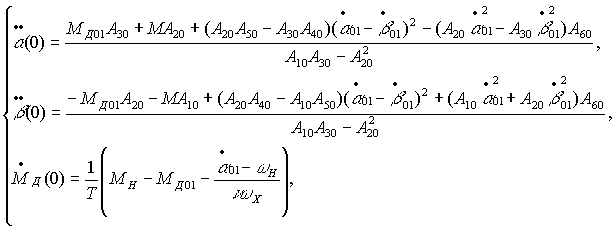
where
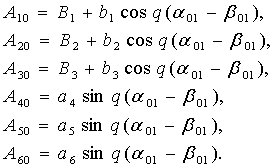
By
differentiating Eq. (1), we find the third derivatives, when 
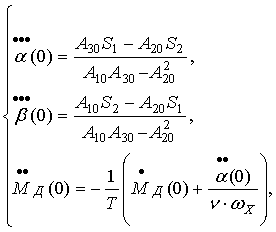
Substituting the
derivatives in Eq. (7), we obtain the final solution of Eq. (1).
In Fig., we plot
the solutions of Eq. (1) [6], obtained
by approximate analytical methods and by the Runge-Kutta methods.
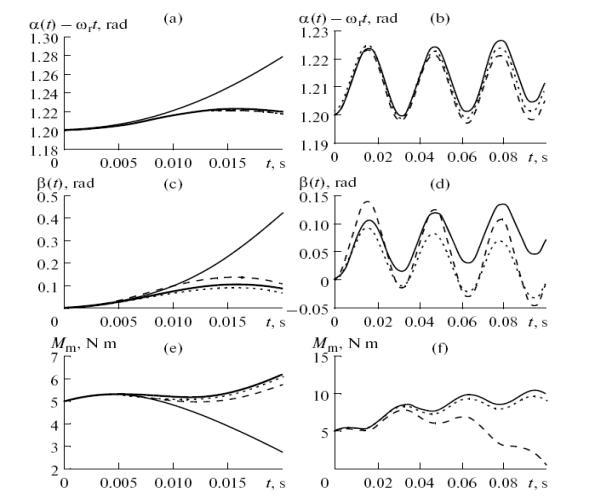
Fig. Dependence of the angles of drive shaft rotation (a, d), and driven
shat rotation (b, e), and motor torque (c, f) on the time t
REFERENCES
1. Leonov A.I.
Inertia-Impulse Automatic Continuously Variable Transmissions, Moscow,
Mashinostroenie, 1978.
2. Alyukov S. V,
Approximate Solution of the Differential Equations of Motion of the Inertial─Pulsed
Transmission. Russian Engineering Research, 2010, Vol. 30, #7.