Экономические
науки/8. Математические методы в экономике
Студентка Лисовская Д.В., 2 курса
Научный руководитель – ассистент Базака Л.Н.
Полесский
государственный университет, Беларусь
Построение регрессионной модели с помощью универсального пакета
программ Statistica
Стабильность цен на потребительском рынке является одним из ключевых
факторов устойчивости макроэкономической ситуации в стране. В соответствии с
Программой социально-экономического развития Республики Беларусь на 2011 – 2015
гг. инфляция по индексу потребительских цен к 2015 году должен составить не
выше 5-6 %. Это предусмотрено Программой деятельности правительства на 2011-
2015 годы [1].
Основным показателем макроэкономической
ситуации является показатель инфляции. Индекс потребительских цен являются
сопутствующими и одним из основных
показателей инфляции.
Целью работы является рассмотрение
основного понятия макроэкономического показателя как индекса потребительских
цен. Его воздействие на макроэкономическую ситуацию: инфляцию, инвестиционную
обстановку, экономический рост.
Мировой опыт свидетельствует, что для
одновременного достижения устойчивости денег, инвестиционной активности и
высокого уровня занятости очень важно, чтобы все участвующие в экономическом
процессе субъекты преследовали цель стабильности и приспосабливали свои
требования к финансово-экономическому потенциалу экономики [5].
На сегодняшний день цель денежной политики
- управление инфляционным процессом рыночными и государственными методами в
интересах подъема национального производства и экономической безопасности
страны. Исходя из мирового опыта, допустима небольшая инфляция, если это
увеличивает платежеспособный спрос и тем самым стимулирует экономический рост
[6].
Особое место при исследовании
экономических явлений между субъектами экономики занимают математические
методы. Они представляют собой инструментарий, позволяющий воспроизводить
реально существующие экономические отношения посредством абстрагирования
незначительных моментов. Отображая различные фрагменты экономических отношений,
математические методы позволяют в то же время исследовать рассматриваемое
экономическое явление с различных позиций
и т.д. [7]. Для выполнения анализа причинно-следственных связей между
экономическими переменными;
прогнозирования значений экономических переменных использовался метод -
основанный на использовании
математических моделей [9].
Для построения этой модели можно применить
универсальный пакет программ Statistica. Данный пакет программ
является универсальной интегрированной системой. Система позволяет выполнять
статистический анализ и визуализацию данных. Содержит широкий набор процедур анализа для применения в научных исследованиях
различных направлений, технике, бизнесе, учебном процессе [2].
При построении модели необходимо включить
те факторы, которые описывают влияние на ИПЦ. Исследование экономических
факторов позволило выявить те факторы, которые имеют наиболее сильную линейную
зависимость c результирующим фактором ИПЦ [3].
Исследовалась зависимость от следующих
потенциальных факторов продуктов питания: мясо и мясопродукты, рыба и
рыбопродукты, молоко и молочные продукты, масло и жиры.
Исходные данные по каждому из показателей
представлены временными рамками за 36 месяцев 2010 – 2012 гг [10].
Таким образом, проведенный анализ,
имеющийся информации и теоретические соображения позволили сформировать
исходный набор факторов, представленных короткими временными рядами.
Таблица 1 - Переменные
|
Переменная |
Фактор |
|
|
Индекс
потребительских цен |
|
|
Мясо
и мясопродукты |
|
|
Рыба
и рыбопродукты |
|
|
Молоко
и молочные продукты |
|
|
Масло
и жиры |
Анализ матриц парных коэффициентов
корреляции позволил выявить статистически значимые линейные и нелинейные
корреляционные связи между исследуемыми переменными. Результаты корреляционного
анализа в целом согласуются с результатом анализа диаграмм рассеивания [4].
Таблица 2 – Матрица парных коэффициентов
корреляции
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0,842102859 |
1 |
|
|
|
|
|
0,911850841 |
0,691639 |
1 |
|
|
|
|
0,68396235 |
0,826386 |
0,423274349 |
1 |
|
|
|
0,666637687 |
0,815498 |
0,539911205 |
0,699516 |
1 |
Результаты корреляционного
анализа свидетельствует о наличии мультиколлинеарности между независимых переменными (сильной
зависимость между факторами). Сильные корреляционные связи были выявлены между
переменными 
и 
, 
и 
. В дальнейшем при построении модели использовались
переменные 
, 
.
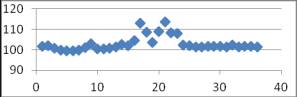
Исследуемые временные ряды представлены на
рисунках.
Рисунок 1 – Временной ряд 
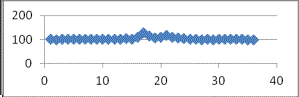
Рисунок 2 – Временной ряд 
Рисунок 3 –
Временной ряд 
Спецификация уравнения регрессионной модели зависимости 
от переменных 
, 
задавалась,
исходя из результатов анализа диаграмм рассеяния и корреляционного анализа
(табл. 2). С помощью метода наименьших квадратов была построена регрессионная
модель.
y=0.26*
+0.37*
+38.16 (1)
t-значения: (5.84) (9.1) (11.06)
R2 =0.92; F(2,33)=182.7038, Fkr=3.284917651, tkr=2.034515297.
Все коэффициенты значимы на уровне 0.05.
Уравнение значимо в целом на уровне 0.05 по F-статистике критерия Фишера.
Коэффициент детерминации равен 0.92. Это значит, что изменения результирующего
фактора на 92 % зависят от изменения
исследуемых факторов, а на долю других факторов приходится 8 % вариаций.
При увеличении переменной 
на одну единицу результативный признак 
(ИПЦ) в средне
увеличится на 0,26.
Полученная модель может быть использована для прогнозирования ИПЦ на краткосрочных
временных интервалах.
Источники
1.
Национальный правовой
интернет-портал Республики Беларусь [Электронный ресурс]/ Минск, 2003 г. –
Режим доступа: http://www.pravo.by/main.aspx?guid=3871&p0=P31100136&p2={NRPA} - Дата
доступа: 20.04.2013.
2.
Прогнозирование в
системе Statistica в среде Window: Основы теории и интенсивная практика на
компьютере: учебное пособие / В.П. Боровиков, Г.И. Ивченко. Под ред.
В.П. Боровиков. – Мн.: Финансы и статистика, 1999. – 382 с.
3. Чернова, Т.В. Экономическая статистика:
учебное пособие: электронная книга / Т.В. Чернова. – Таганрог: Изд-во
ТРТУ, 1999. – 140 с.
4.
Белов, А. А. Теория
вероятностей и математическая статистика: учебник / А.А. Белов,
Б.А. Баллод, Н.Н. Елизарова. – Ростов-на-Дону: Феникс, 2008. - 318 с.
5.
Инюшин, В.
Денежно-кредитное регулирование в условиях глобализации: статья /
В. Инюшин – «Полярная звезда», 2002. – с. 1-14.
6.
Борисов, А.Б. Большой
экономический словарь / А.Б. Борисов. – М.: Книжный мир, 2003. – 895 с.
7.
Замков, О.О.
Математические методы в экономике / О.О. Замков, А.В. Толстопятенко,
Ю.И. Черемных. – М.: МГУ им. М.В.
Ломоносова, Изд-во «ДИС», 1997.
8.
Тихомиров, Н.П.
Методы социально-экономического прогнозирования / Н.П. Тихомиров,
В.А. Попов – М.: Изд-во ВЗПИ, А/О «Росвузнаука», 1992.
9.
Крук, Д.М. Основы экономического и
социального прогнозирования / Д.М. Крук, Лукин B.C., Мосин В.И.
и др. – М.: Высшая школа, 1985.
10. Национальный
статистический комитет Республики Беларусь [Электронный ресурс]/ Минск,
1998-2013 гг. – Режим доступа: http://belstat.gov.by/ - Дата доступа: 13.03.2013