Магистрант  Елешова-Турсунова А.Е.

«Тұран-Астана» университеті, Қазақстан

 

Конструкция элементтерінің қолданбалы есептеу теориялары

Жазық элемент осы жазықтыққа перпендикуляр (көлденең) жүктеме әсерінен иіле алатын пластина деп аталады. Осы пластинаны координаттық жүйеде  қарастырайық: - пластинаның координаттық өстер  бойындағы өлшемдері (қабырғаларының ұзындықтары);  - координаттық өс  бойындағы өлшемі (пластинаның қалыңдылығы). Жазықтық  пластинаның орта (бейтарап) жазықтығы болып табылады да сыртқы көлденең күштер әсерінен пластинаның иілуінде бетке айналады. Өлшемдердің  шамалары бір – біріне парапар  болғандықтан  және  пластинаның тәуелсіз өлшемдері болып табылады. Пластинаның қалыңдылығы  оған тікелей әсер етеді: егер  болса, онда пластина қалың болады (қалың пластина); егер  болса, онда пластина өте жұқа болады (жарғақ); егер  болса, онда пластина жұқа болады (жұқа); егер үлкен майысу – () болса, онда пластина қатты деп аталынады; егер  болса, онда пластина майысқақ болады. Ұсынылып отырған нақтыланған классикалық теория келесі болжамдарға негізделген:

-         көлденең қысылу заңдылық бойынша өзгереді:

,                                             (1)

 - көлденең қысым параметрі;  - көлденең өлшемсіз координата;  - негізгі майысу функциясы;  - координаттық өс  бойымен бағытталған жылжу; көлденің ығысулар (сырғулар) белгілі деп саналынады.

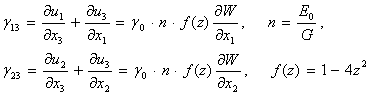                    (2)

мұнда  - көлденең ығысу параметрі;  - серпімділік тұрақтылар параметрі;  - көлденең ығысу таралу функциясы; көлденең қысым тангенциалдық деформацияларға пропорционал болады.     (3)мұнда  - көлденең қысым параметрі. Егер  болса, осы теорияның дербес түрі болып белгілі классикалық (техникалық) теория табылады.

Жылжулар мен деформациялар. Болжам (1) – ді интегралдау және шартты  ескеру арқылы көлденең жылжу функциясын анықтаймыз      (4) Табылған жылжуды (4) болжам (2) – ге енгізіп оны интегралдау арқылы және шарттарды (бейтарап жазықтық созылмайды немесе қысылмайды)  қолдану арқылы тангенциалдық жылжуларды табамыз:

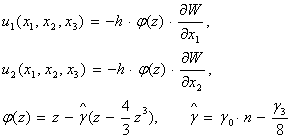                        (5)

мұнда - тангенциалдық жылжулар таралу функциясы. Осы жылжуларды (4) және (5) ескере отырып серпімділік теориясының формулалары бойынша деформацияларды анықтаймыз:

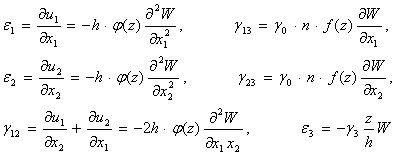               (6)

Осы алты деформациялардың үшеуі  қабылданып және үшеуі  анықталынады. Кернеулер мен ішкі күштер. Гуктың жалпы заңдары пластинаның материалы изотропты болғанда былайша жазылады.

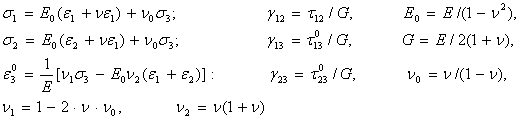         (7)

мұнда  - пластинаның материалының серпімділік модулі мен Пуассон коэффициенті. Осы заңдардың кейбірлерін болжам (3) бойынша келесі түрге келтіруге болады:

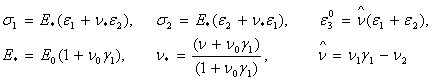                 (8)

 - жалпыланған серпімділік модулі мен Пуассон коэффициенті.

Деформациялар компоненттерін (6) өрнектерге (7) және (8) – ге енгізу арқылы кернеулер компоненттерін табамыз.

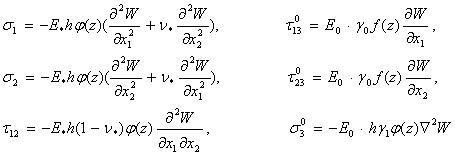             (9)

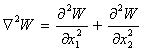 - Лаплас операторы.

Жанамалық кернеудің  ығысу модулі былайша түрлендірілген:

Көлденең нормальдық және жанамалық кернеулер компоненттері кернеулік тепе – теңдік теңдеулеріне

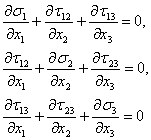
(9) – шы өрнектегі кернеулерді  енгізіп, оларды интегралдау арқылы анықталады:

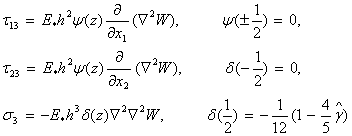                                    (10)

мұнда ,  - жанамалық және нормалды кернеулердің таралу функциялары. Ішкі күштер компоненттері тең болады:

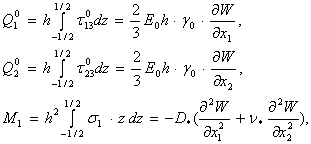                                            (11)

мұнда  - пластинаның жалпыланған цилиндрлік қатаңдығы. Кернеулер (9) және (10) ішкі күштер (11) арқылы былайша анықталады:

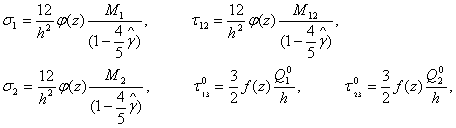   (12)

мұнда  - тепе-теңдік теңдеулерін, ал  - Гук заңдарын қанағаттандыратын кернеулер. Егер тангенциалдық деформацияларды келесі түрде қабылдап алатын болсақ,

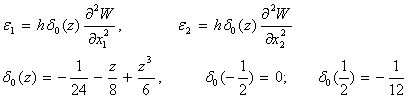   (13)

онда болжам (3) бойынша анықталатын кернеу тең болады.               (14) Гук заңы бойынша анықталатын көлденең деформация (8) деформацияларды (6) ескеру арқылы былайша жазылады:

          (15) Пластинаның жалпыланған цилиндрлік қатаңдығын (11) жалпыланған серпімділік модулін (8) ескеру арқылы келесі түрге келтіруге болады:

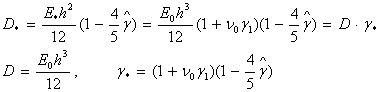                              (16)

 - пластинаның классикалық теориясындағы цилиндрлік қатаңдығы;  - жалпыланған қатаңдық параметрі.

Пластинаның дифференциалдық тепе-теңдік теңдеуі мен шекаралық шарттары. Тепе-теңдік теңдеуін алу үшін көлденең нормалдық кернеудің шекаралық шарттарын қолданамыз:  мұнда  - пластинаға әсер ететін жүктеменің қарқындылығы. Осы шартқа (10) өрнекті енгізу арқылы мынаны аламыз  яғни    (17) мұнда  - пластинаның жалпыланған цилиндрлік қатаңдығы (16). Осы теңдеу пластинаның иілуінің дифференциалдық теңдеуі болып табылады. Пластинаның бұрылу бұрыштары  жылжулардың (5) интегралдық сипаттамалары болып табылады.

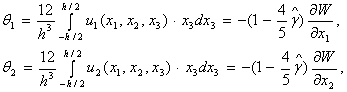      (18)

Пластинаның жақтарында  түрлі бекіністер болуы мүмкін. Олардың негізгілері болып  табылады:

1)                Топсалы бекініс

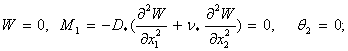                                    (19)

2)                Қатты бекініс

                         (20)

3)                Бекініссіз (бос)

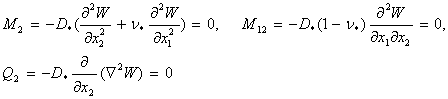                       (21)

4) Тірелген

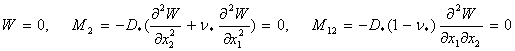 (22)

Осы шарттар пластинаның негізгі шекаралық шарттары болып табылады. Сөйтіп, пластинаның иілуін сипаттайтын майысу функциясы  теңдеуді (17) шекаралық шарттардың (19)-(22) бірін қанағаттандыру арқылы анықталады. Сөйтіп, нақтыланған классикалық теория бойынша факторларды көлденең қысым , сырғу  және қысылу  оңай ескеруге болады. Осы теорияның дербес түрі болып көпшілікке мәлім классикалық теория  табылады. Оның басқа теориялардан [1] айырмашылығы есептеу формулалары классикалық теориядағындай болатындығында.

Әдебиеттер:

1.     Александров А.В., Потапов В.Д. Основы теории упругости и пластичности. –М.:Высшая школа, 1990. -400с.

2.     Тимошенко С.П., Войновский – Кригер С. Пластинки и оболочки. –М.: Физматгиз. 1963. -635с.

3.     Турсунов К.А., Турсунов А.К. Основы расчета плоских элементов конструкций. - Караганда.: КарГУ, 2000. - 41с.

4.     Турсунов К.А. Об одном методу расчета изгибаемой пластины. Вестник КарГУ, №3(27)/2002, с.14-21.