Экономические науки/8. Математические методы в экономике.

Шевченко Я.Т., д.т.н Бідюк П.І.

Національний технічний університет України «Київський політехнічний інститут», Україна

ПОБУДОВА ІНФОРМАЦІЙНО — АНАЛІТИЧНОЇ СИСТЕМИ АДАПТИВНОГО ПРОГНОЗУВАННЯ ФІНАНСОВИХ ПРОЦЕСІВ ТА ЇЇ ЗАСТОСУВАННЯ

Вступ. Розв’язання задач ефективного прогнозування на новому якісному рівні вимагає застосування сучасних методів системного аналізу до існуючих підходів та методів, коректного використання методів математичного моделювання на основі досягнень теорії оцінювання та статистичного аналізу даних. Деякі можливості розв’язання задачі адаптивного прогнозування розглядаються в роботах [1, 2, 3]. Однак, методи, представлені в цих роботах, фактично не дають відповіді на основне запитання: як організувати процес обробки даних таким чином, щоб отримати кращі оцінки прогнозів в умовах наявності невизначеностей структурного, параметричного і статистичного характеру? Подібні невизначеності можуть бути зумовлені нестаціонарністю процесу, пропусками даних, неякісними зашумленими даними, екстремальними значеннями та ін.

Актуальність. Існуючі методи прогнозування, які ґрунтуються на аналітичних процедурах, логічних правилах та раціональному експертному мисленні, у багатьох випадках не дають бажаного результату стосовно якості оцінок прогнозів, а тому виникає проблема значного і прискореного підвищення якості коротко- та середньострокового прогнозування.

Постановка задачі. Необхідно розробити концепцію адаптивного прогнозування процесів довільної природи на основі підходів та методів системного аналізу, які передбачають ієрархічний аналіз процесів моделювання та прогнозування, врахування невизначеностей структурного параметричного і статистичного характеру, адаптування моделей до змін у процесах з метою пошуку кращих оцінок прогнозів за допомогою множини числових критеріїв їх якості. Запропонувати нові обчислювальні схеми побудови прогнозуючих систем із зворотним зв’язком на основі використання статистичних параметрів якості моделей та оцінок прогнозів.

Побудова інформаційно-аналітичної системи для порівняння методів прогнозування фінансових процесів та методика розв’язання задачі. Спрощена концептуальна схема процесу моделювання, прогнозування та керування (як логічного завершення двох попередніх етапів) наведена на рис. 1. Розглянемо докладніше кожний з етапів. Створення системи адаптивного прогнозування починається з вибору процесу, аналізу його поточного стану, існуючих моделей та підходів до прогнозування його розвитку. Це можуть бути математичні моделі у вигляді систем рівнянь, закони розподілу вхідних та вихідних величин (статистистичні моделі) або логічні моделі у вигляді наборів правил, які характеризують взаємодію входів і виходів.

Так, модель, створена на основі теоретичних уявлень і закономірностей стосовно конкретного процесу, може потребувати лише деякого уточнення її параметрів за допомогою статистичних даних. А модель, яка повністю грунтується на статистичних дослідженнях, може потребувати значно більших об’ємів інформації та часу для її побудови. Огляд літературних джерел також може бути корисним з точки зору вибору методів адаптивного оцінювання параметрів моделі. Кожний метод має свої особливості та межі застосування, а тому необхідно знати ці особливості до його застосування на практиці.

Формування даних

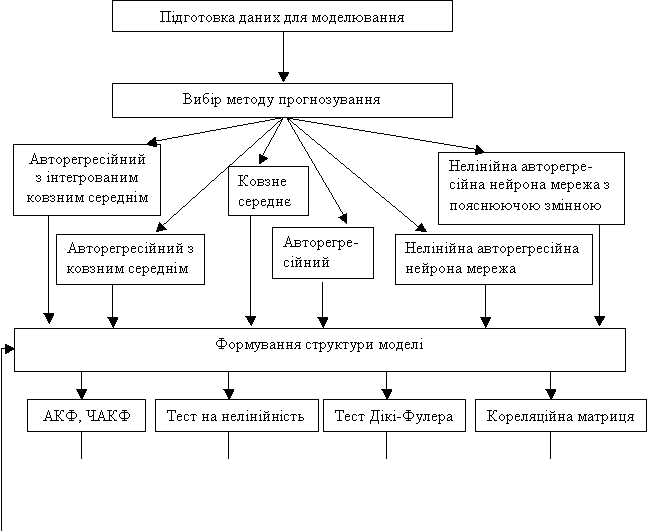
Критерії якості моделі

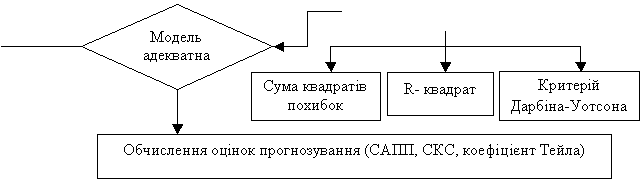
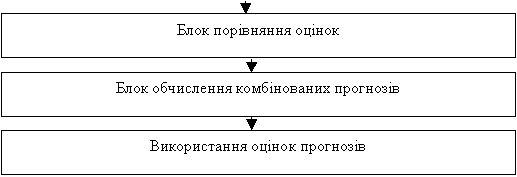
Рис. 1. Схема адаптивного оцінювання моделі

Практика створення прогнозуючих систем для процесів довільної природи свідчить про те, що готові до використання моделі зустрічаються дуже рідко. Навіть існуючі апробовані моделі потребують корегування їх структури та/або параметрів з метою їх адаптування до конкретних умов. Тому в більшості випадків необхідно будувати нову модель на основі наявних статистичних даних. Якість даних відіграє надзвичайно важливу роль при побудові математичної моделі, а тому при зборі даних необхідно керуватись відомими вимогами стосовно їх інформативності, синхронності та коректності [4].

Попередня обробка даних необхідна для приведення їх до форми, яка забезпечить можливості коректного застосування методів оцінювання параметрів моделі та отримання їх статистично значущих оцінок. Так, досить часто необхідно заповнювати пропуски даних, корегувати значні імпульсні (екстремальні) значення, нормувати значення у заданих межах, логарифмувати великі значення та фільтрувати шумові складові.

На основі даних, коректно підготовлених для подальших обчислювальних процедур, оцінюють структури та параметри математичних моделей-кандидатів процесів, вибраних для прогнозування та керування. Вибір (оцінювання) структури моделі – ключовий момент її побудови. Нагадаємо, що структура моделі включає п’ять елементів: (1) вимірність (число рівнянь, які утворюють модель); (2) порядок – максимальний порядок диференціальних або різницевих рівнянь, які входять в модель; (3) нелінійність та її тип (нелінійності відносно змінних або параметрів); (4) час затримки (лаг) реакції відносно входу та його оцінка; (5) зовнішнє збурення процесу та його тип (детерміноване або випадкове) [5]. Як правило, для одного процесу оцінюють декілька моделей-кандидатів, а потім вибирають з них кращу за допомогою множини статистичних параметрів якості моделі.

Більшість процесів в техніці, економіці та фінансах мають детерміновану та випадкову складові. Тому як статистичну модель будемо розуміти модель процесу у вигляді розподілу випадкових величин [5]. Обґрунтований вибір типу розподілу та оцінювання його параметрів за допомогою експериментальних даних представляє собою процес побудови статистичної моделі процесу.

Побудована модель ще не гарантує високої якості оцінок прогнозів. Тому після побудови модель необхідно перевірити на можливість застосування до розв’язання задачі прогнозування. На сьогодні існує широкий спектр методів прогнозування, які застосовують в економіці та фінансах. Однак, далеко не всі методи забезпечують високоякісні прогнози у конкретних випадках їх застосування. Тому вибір методу прогнозування – це досить непроста задача, яка часто потребує одночасного застосування декількох альтернатив і вибору кращого результату.

Самими популярними на сьогодні методами прогнозування розвитку процесів довільної природи є такі: методи регресійного аналізу, нечітка логіка, ймовірнісні методи, метод групового врахування аргументів (МГВА), нейронні мережі, методи на основі „м’яких” обчислень, метод подібних траєкторій та деякі інші. Кожний із згаданих методів в тій чи іншій мірі може враховувати невизначеності структурного, статистичного або параметричного характеру. За своєю природою ці методи близькі до способів моделювання ситуацій та прийняття рішень людиною, а тому їх застосування в системах управління та підтримки прийняття рішень (СППР) можуть дати значний позитивний ефект.

Аналіз якості моделі і прогнозу. Якість моделі оцінюють за допомогою декількох статистичних критеріїв якості, зокрема таких: коефіцієнта множинної детермінації (), який характеризує інформативність моделі по відношенню до інформативності даних; статистики Дарбіна-Уотсона (), що визначає ступінь автокорельованості похибок моделі; інформаційного критерію Акайке (), суми квадратів похибок моделі (), та інших.

Важливим моментом процесу прогнозування є об’єктивне визначення якості отриманого прогнозу. Оскільки оцінки прогнозів – це випадкові величини, то для визначення їх якості використовують множину статистичних критеріїв. Досить часто якість оцінок прогнозів визначають лише за допомогою середньоквадратичної похибки (СКП). Однак, значення СКП залежить від масштабу даних, а тому цієї характеристики недостатньо для аналізу якості прогнозу. Поглиблене оцінювання якості прогнозів досягається за рахунок використання критеріїв, які дають відносні оцінки якості (наприклад, коефіцієнт Тейла) та відносні оцінки в процентах (наприклад, ). Перевагою їх використання є те, що вони не залежать від масштабу даних. і коефіцієнт Тейла обчислюють за виразами:

,

,

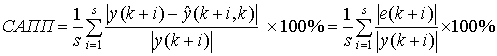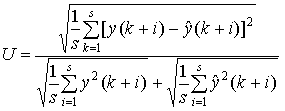де число кроків прогнозування; фактичні значення даних; оцінки прогнозів. Коефіцієнт Тейла – це важливий індикатор якості моделі і прогнозу; за означенням, . При оцінки прогнозів наближаються до фактичних значень ряду і модель має високу ступінь адекватності. Тобто дає можливість встановити придатність моделі (методу) для оцінювання прогнозу в принципі. У багатьох випадках кращих результатів прогнозування можна досягти за рахунок усереднення (або комбінування за допомогою вагових коефіцієнтів) оцінок прогнозів, отриманих за допомогою різних методів.

Адаптивне обчислення оцінок прогнозів. Для збереження якості оцінок прогнозів в умовах нестаціонарності досліджуваного процесу, а також для підвищення якості прогнозування процесів з довільними статистичними характеристиками необхідно застосовувати адаптивні схеми оцінювання прогнозів. Вихідними величинами для аналізу якості прогнозів та формування адаптивних схем їх оцінювання є значення похибок прогнозів та їх статистичні характеристики. Для розв’язання задачі адаптації прогнозуючої моделі до вимог стосовно якості прогнозу можна скористатись такими обчислювальними можливостями:

– рекурсивне оцінювання параметрів моделей, що сприяє уточненню моделі та підвищенню якості прогнозу;

– автоматизований аналіз часткової автокореляційної функції (ЧАКФ) , автокореляційної функції(АКФ)

– автоматизований аналіз функції взаємної кореляції

– автоматизований тест Дікі –Фулера

– почергове введення в модель можливих регресорів та аналіз їх впливу на якість прогнозу.

Застосування тієї чи іншої схеми обчислень залежить від конкретної постановки задачі, якості та об’єму експериментальних (статистичних) даних, сформульованих вимог до якості оцінок прогнозів та часу, наявного для виконання обчислень. Кожний метод адаптивного формування оцінки прогнозу має свої особливості, які мають бути враховані при створенні системи адаптивного прогнозування.

Приклад застосування концепції адаптивного прогнозування до процесів ціноутворення на біржі. У даному прикладі будуть розглянуті котування компаній з S&P 500 на біржі NASDAQ.

У таблицях 1-6 будуть приведені середні значення показників якості моделі і показників якості прогнозу для 100 вибірок.

Розглянемо спочатку авто-регресійну модель. Для кожної моделі порядок авторегресійної складової буде обраний автоматично. Для цього введемо кількість лагів ЧАКФ для аналізу 10 та межу значимості, яка визначає, що значення ЧАКФ статистично відмінне від нуля на рівні 0,2.

Таблиця 1

Авторегресійна модель

Довжина кожної вибірки	100
Горизонт прогнозу	10
Кість лагів ЧАКФ	10
Межа значимості ЧАКФ	0,2
Статистика Дорбіна - Уотсона	2.05258
R - квадрат	0.972833
Сума квадратів похибок	99.771
Середньоквадратична похибка	1.42361
Середньоарифметична процентна похибка	3.141 %
Коефіцієнт Тейла	0.00053835
Критерій Акайке	5.9435

Далі проведемо аналіз тих самих вибірок застосовуючи модель ковзного середнього. Порядок моделі визначається за допомогою функції взаємної кореляції, визначаючи останній лаг, що більше за межу значимості.

Таблиця 2

Модель з ковзним середнім

Довжина кожної вибірки	100
Горизонт прогнозу	10
Ширина вікна функції взаємної кореляції	3
Кількість лагів функції взаємної кореляції	10
Межа значимості функції взаємної кореляції	0,2
Статистика Дорбіна - Уотсона	1.53464
R - квадрат	0.964273
Сума квадратів похибок	145.816
Середньоквадратична похибка	4.35648
Середньоарифметична процентна похибка	9.5748 %
Коефіцієнт Тейла	0.00143977
Критерій Акайке	9.0566

Якість моделі та якість прогнозу значно погіршилися по всім показним. Далі виконаємо побудову автегресійнихмоделі з ковзним середнім.

Таблиця 3

Авторегресійна модель з ковзним середнім

Довжина кожної вибірки	100
Горизонт прогнозу	10
Ширина вікна функції взаємної кореляції	3
Кількість лагів функції взаємної кореляції	10
Межа значимості функції взаємної кореляції	0,2
Кількість лагів ЧАКФ	10
Межа значимості ЧАКФ	0,2
Критерій Дарбіна - Уотсона	1.95258
R - квадрат	0.942833
Сума квадратів похибок	104.771
Середньоквадратична похибка	1.46361
Середньоарифметична процентна похибка	3.341 %
Коефіцієнт Тейла	0.00073234
Критерій Акайке	6.0835

За допомогою АРКС моделі були отримані кращі моделі і прогнози, ніж за допомогою КС моделі, але АРКС модель не враховує наявність одиничних коренів. Проведемо тест Дікі-Фулера для автоматичного вибору порядку авторегресійної моделі з інтегрованим ковзним середнім. Порядок авторегресійної частини та ковзного середнього визначається автоматично так само, як в моделях АР і КС відповідно.

Таблиця 4

Авторегресійна модель з інтегрованим ковзним середнім

Довжина кожної вибірки	100
Горизонт прогнозу	10
Ширина вікна функції взаємної кореляції	3
Кількість лагів функції взаємної кореляції	10
Межа значимості функції взаємної кореляції	0,2
Кількість лагів ЧАКФ	10
Межа значимості ЧАКФ	0,2
Критерій Дарбіна - Уотсона	1.99268
R - квадрат	0.983433
Сума квадратів похибок	94.368
Середньоквадратична похибка	1.54912
Середньоарифметична процентна похибка	1.931 %
Коефіцієнт Тейла	0.00023234
Критерій Акайке	3.5835

Результати АРІКС моделі найкращі серед усіх розглянутих регресійних моделей. Це може бути пояснено не стаціонарністю процесу формування котувань на фондовій біржі, а, отже, необхідністю врахування одиничних коренів.

Таблиця 5

Нелінійна авторегресійна нейронна мережа

Довжина кожної вибірки	100
Горизонт прогнозу (тестова вибірка)	10
Тренувальна вибірка	85
Перевірочна вибірка	15
Кількість прихованих нейронів	10
Кількість затримок	2
Критерій Дарбіна - Уотсона	2.02298
R - квадрат	0.989733
Сума квадратів похибок	90.578
Середньоквадратична похибка	1.36012
Середньоарифметична процентна похибка	1.731 %
Коефіцієнт Тейла	0.00092347
Критерій Акайке	2.81234

Нейронна мережа дала значно кращі результати за авторегресійні моделі, що може бути пояснено наявністю прихованих закономірностей у процесах утворення котувань на фондовому ринку.

Побудуємо модель нелінійна авторегресійної нейронної мережі з пояснюючою змінною. У якості пояснюючої змінної використаємо індекс S&P 500.

Таблиця 6

Нелінійна авторегресійна нейронна мережа з пояснюючою змінною

Довжина кожної вибірки	100
Горизонт прогнозу (тестова вибірка)	10
Тренувальна вибірка	85
Перевірочна вибірка	15
Кількість прихованих нейронів	10
Кількість затримок	2
Критерій Дарбіна - Уотсона	2.019324
R - квадрат	0.988732
Сума квадратів похибок	88.395
Середньоквадратична похибка	1.3134
Середньоарифметична процентна похибка	1.711 %
Коефіцієнт Тейла	0.00098437
Критерій Акайке	2.81234

Порівняємо критерії якості прогнозу для всіх моделей.

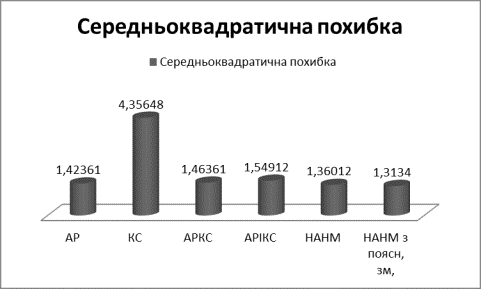
Рис.1 Середньоквадратична похибка

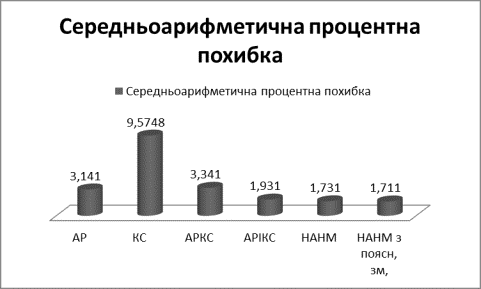
Рис.2 Середньоарифметична процентна похибка

Як видно з рис 1-2: найкращі прогнози отримано за допомогою нейромереж та АРІКС моделі, що може бути пояснено складними прихованими закономірностями, що з’являються при формуванні котувань на фондових біржах, а також нестаціонарною структурою вибірок.

Висновки. Запропонована концепція формулювання та розв’язання задач адаптивного прогнозування ґрунтується на комплексному використанні методів попередньої обробки і аналізу даних, математичного і статистичного моделювання, прогнозування. Циклічне адаптування моделі до процесу на основі застосування множини статистичних характеристик процесу, зокрема, кореляційних та автокореляційних функцій забезпечує отримання високоякісних коротко- та середньострокових прогнозів за умови наявності інформативних даних.

Побудовано математичні моделі високого ступеня адекватності для процесів формування котувань на фондовій біржі. Запропоновано метод побудови регресійних моделей з використанням схеми адаптивного прогнозування.

В подальших дослідженнях доцільно розглянути моделі інших типів, а також застосувати удосконалені схеми адаптивного прогнозування з можливістю покращення якості попередньої обробки вхідних даних, що використовуються для побудови моделей.

Література

1. Box, G.E.P., G.M. Jenkins, and G.C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice-Hall, 1994.

2. W.A. Brock, J.A. Scheinkman, W.D. Dechert and B. LeBaron. "A Test for Independence based on the Correlation Dimension". 15:197-235, 1996.

3. Chatfield C. Time series forecasting. – London: Chapman & Hall, 2000. – 267 p.

4. Altman E.I., Avery R.B., Eisenbeis R.A., Sinkey J. Application of Classification Techniques in Business, Banking and Finance. – Greenwich: JAI Press, 1981 – 418 p.

5. Бидюк П.И., Романенко В.Д., Тимощук О.Л., Учебное пособие по "Анализу временных рядов" - НТУУ "КПИ", 2010, 230 с.

6. Hosmer D.W., Lemeshow S. Applied Logistic Regression. – New York: John Wiley & Sons, Inc., 2000. – 380 p.