Современные информационные технологии/3.Программное обеспечение

Сергатая И.Ю.

ГВУЗ «Национальный горный университет», Днепропетровск, Украина

Исследование применение метода для обработки слабоконтрастных изображений в пространстве модели эллипсометрических параметров Стокса.

Для области цифровой обработки изображений большой интерес представляет возможность исследования применения виртуальных физических методов для обработки и анализа слабоконтрастных изображений. Эти методы обладают наибольшей чувствительностью к незначительным вариациям физических параметров исследуемых объектов, в частности, эллипсометрические методы измерений.

Виртуальная реализация «эллипсометрического подхода» основана на свойствах поляризованной электромагнитной волны. Известно, что электрический вектор соответствует волне, в комплексном представлении описываемой выражением

, (1)

Тогда в каждой точке пространства вектор E описывает замкнутую кривую, являющуюся эллипсом, уравнение которого имеет вид

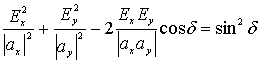, (2)

где ; ; Если и , то эллипс вырождается в окружность (круговая поляризация), а если , то он вырождается в прямую линию (линейная поляризация).

Таким образом, поле в каждой точке характеризуется плоскостью, в которой лежит его эллипс поляризации, который может быть полностью охарактеризован параметрами Стокса определяемыми как

; ; (3)

Параметр пропорционален интенсивности анализируемого изображения, а можно интерпретировать как декартовы координаты точки на сфере радиусом известной как сфера Пуанкаре.

Структура алгоритма для реализации виртуального эллипсометрического метода для слабоконтрастных изображений включает в себя следующие этапы.

1. Модуляционное преобразование исходного изображения

(4)

позволяет сопоставить каждому пикселю анализируемого изображения две ортогональные компоненты векторного поля – действительная и мнимая части выражения

,

которые интерпретируются в виде аналога ортогональных составляющих и в выражениях (2) и (3), соответственно.

2. Фазовая компонента вычисляется следующим образом

, (5)

где H – оператор эквализации (выравнивания) гистограммы исходного изображения , – стабилизирующий параметр (выбирался равным 0.001).

3. Синтез четырех эллипсометрических характеристик и исходного изображения на основе использования выражения (3) .

4. Визуализация и анализ новых виртуальных изображений, полученных на основе эллипсометрических характеристик.

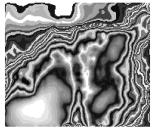
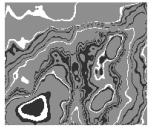
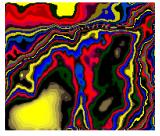
На рис. 2. представлены эллипсометрические характеристики, полученные для геофизического потенциального электрического поля, из рассмотрения которых видно, что они являются очень чувствительными к изменению исходной яркости и обеспечивают высокую детализацию изображения.

Рис. 2. Эллипсометрический синтез в пространстве параметров Стокса геофизического поля

Таким образом, отображение анализируемых слабоконтрастных изображений в пространстве самоорганизующихся эллипсометрических параметров Стокса обеспечивает дополнительные информационные возможности, которые повышают степень чувствительности и надежности анализа, обеспечивают высокую детализацию изображения.

Литература:

1. Аззам Р. Эллипсометрия и поляризованный свет / Р. Аззам, Н. Башара; под ред. А.В. Ржанова., К.К. Свиташева. – М.: Мир, 1981. – 583 с.

2. Основы эллипсометрии / [под ред. А.В. Ржанова]. – Новосибирск: Наука, 1979. – 422 с.

3. Шовенгердт Р.А. Дистанционное зондирование. Модели и методы обработки изображений / Р.А. Шовенгердт; [пер с англ. И.А. Громова]. – М.: Техносфера. – 2010. – 560 с.