УДК 517.95

N - солитонные решения для 3-х мерного нелинейного уравнения

Сурнева О.Б.

Для построения солитонных решений будем использовать алгоритм метода Хироты [1]:

1. Произвести замену зависимой переменной, так чтобы уравнение имело билинейную форму.

2. Рассмотреть формальные ряды теории возмущений.

3. Построить 1- солитонное решение, провести исследования и доказать существование N- солитонных решений.

ЛЕММА 1. Нелинейное уравнение в частных производных

(1)

где - произвольная постоянная, а - неизвестная функция, с помощью замены 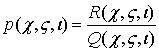приводится к однородному виду

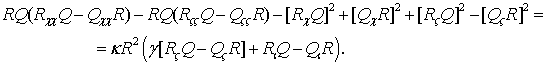(2)

ЛЕММА 2. Выражение (2) эквивалентно однородному уравнению

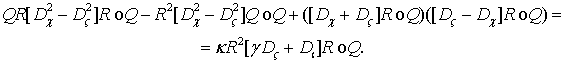(3)

где в записи использован оператор дифференцирования Хироты: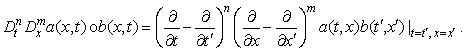

ДОКАЗАТЕЛЬСТВО. Используя, операторы дифференцирования Хироты

выделим в равенстве (2) следующие связи:

,

, .

Выполним соответствующую подстановку в имеющемся уравнении (2)

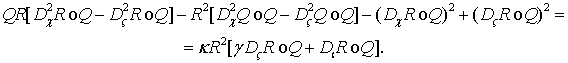(4)

Сгруппируем операторы, связанные отдельно с упорядоченной парой функций и отдельно с парой в результате получим связь (3). Полученное выражение однородно относительно , все слагаемые имеют четвертый порядок.

ЛЕММА 3. Выражение (3) эквивалентно системе уравнений

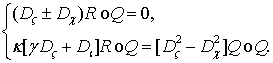(5)

ДОКАЗАТЕЛЬСТВО. Сгруппируем элементы с , а так же первое и третье слагаемые (3) и вынесем общий множитель справа

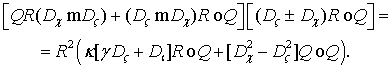
Так как полученное равенство имеет две неизвестные функции, то, очевидно, что оно распадается на систему

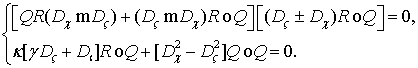(6)

В первом равенстве системы первая скобка представляет собой оператор, тогда для того чтобы первое равенство системы (6) выполнялось достаточно положить , в результате имеем систему (5).

Посмотрим, возможно, ли применение алгоритма Хироты для построения 1-солитонного решения.

Точное решение уравнения (1) можно построить в виде обрывающихся рядов теории возмущений по некоторому малому параметру . Представим функции в виде таких рядов:

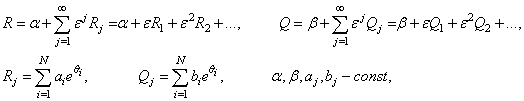(7)

где .

Для получения одно - солитонного решения положим и, считая , ряды (7) обрываются, тогда

(8)

ТЕОРЕМА 1. Нелинейное уравнение (1) имеет одно - солитонное решение

,

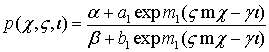где произвольные постоянные.

ДОКАЗАТЕЛЬСТВО. При , представляем в виде (8). Подставим полученные в систему (5), тогда получим в первом равенстве посте взятия производных:

(9)

Аналогично поступим и со вторым равенством системы (5), после приведения подобных имеется только член с показательной функцией

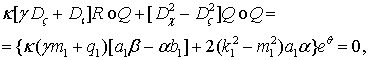(10)

В результате объединения (9) и (10) операторная система (5) перешла в систему на определение неизвестных параметров

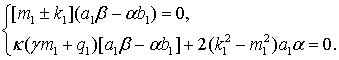(11)

Полученная система имеет большую степень произвола, проанализируем, какие возможности решения здесь имеются.

Если предположить, что и первое равенство обращается в нуль, то это приведет к пропорциональности коэффициентов и отношение 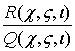даст просто постоянную, поэтому и, следовательно

. (12)

Отсюда получаем, что система уравнений (11) выполняется тождественно только при

. (13)

В результате получено точное решение

.

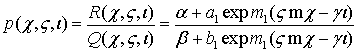ТЕОРЕМА 2. Нелинейное уравнение (1) имеет точное решение вида

,

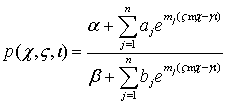где произвольные постоянные.

ДОКАЗАТЕЛЬСТВО. Для получения двухсолитонного решения положим и, считая, что ряды (7) обрываются, положим

, (14)

Подставим вид (14) в систему (5), тогда получим первое и второе равенство после взятия производных тождественно обращаются в нуль.

Аналогичные рассуждения приводят к тождественному выполнению системы (5) при , следовательно, теорема верна при любом значении .

Литература

1. Абловиц М., Сигур Х. Солитоны и метод обратной задачи. - М.: Мир, 1987.