К. ф.-м. н. Мирская Е.И.,

к. ф.-м. н. Марзан С.А.

Брестский государственный университет имени А.С. Пушкина,

Республика Беларусь

СРАВНИТЕЛЬНЫЙ АНАЛИЗ ДИСПЕРСИИ ОЦЕНКИ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ В ЗАВИСИМОСТИ ОТ

ОКОН ПРОСМОТРА ДАННЫХ

Исследование статистических оценок спектральных плотностей является одной из классических задач анализа временных рядов.

Среди непараметрических методов спектрального оценивания одним из наиболее распространенных является метод Уэлча [1]. Этот метод предполагает деление временного ряда на интервалы и вычисление периодограммы для каждого из них. Итоговая оценка получается путем осреднения отдельных периодограмм. Введение такой процедуры осреднения позволяет уменьшить дисперсию оценки в число раз, равное числу интервалов разбиения.

Рассмотрим r-мерный стационарный случайный процесс , , с , , неизвестной взаимной спектральной плотностью , , .

Пусть − последовательных наблюдений за составляющей процесса , , , и , где − число пересекающихся интервалов разбиения длины .

В качестве оценки взаимной спектральной плотности процесса исследована статистика вида

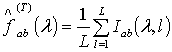, (1)

где

,

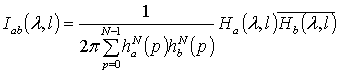, , , модифицированная периодограмма на −ом интервале разбиения, а задано выражением

, , , .

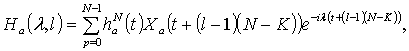
Исследовано асимптотическое поведение дисперсии оценки (1).

Теорема 1. Если взаимная спектральная плотность , ,

непрерывна в точке и ограничена на , семиинвариантная спектральная плотность 4−го порядка ограничена на , окна просмотра данных , ограничены единицей и имеют ограниченную вариацию, выполняется соотношение

, (2)

то для оценки , , заданной выражением (1), справедливо соотношение

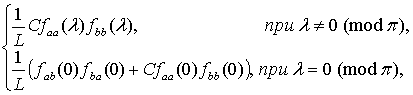
где − некоторая постоянная, , .

Доказательство. В соответствии с работой [2] ковариация оценки , , , может быть представлена в виде суммы трех слагаемых , и . Рассмотрим каждое из слагаемых.

Учитывая, что семиинвариантная спектральная плотность 4-го порядка ограничена, выполняется соотношение (2), можно показать, что .

Рассмотрим случай: . Учитывая непрерывность взаимной спектральной плотности в точке , используя неравенство Гельдера, и так как ограничена на , получим, что

, .

Рассмотрим случай: . Аналогично можно показать, что

, .

Теорема доказана.

С помощью математического пакета Matlab для конкретного временного ряда был проведен сравнительный анализ дисперсии оценки (1) для окон просмотра данных Блэкмана, Хэмминга, Тьюки для 50%-ного перекрытия интервалов. Показано, что дисперсия оценки минимальна при использовании окна просмотра данных Тьюки.

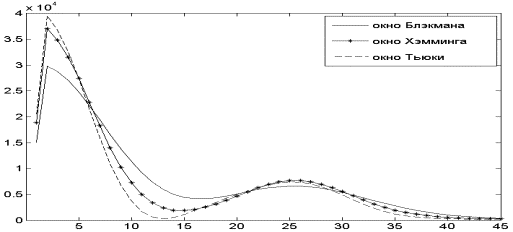
Рисунок – 1 График оценки спектральной плотности, построенной по 50 наблюдениям групп солнечных пятен за период с 1940 по 1990 год.

СПИСОК литературы

1. Welch, P. D. The use of FFT for the estimation of power spectra / P.D.Welch // IEEE Trans. Electroacoust. – 1967. – V. 15, № 2. – Р. 70–73.

2. Труш, Н.Н. Асимптотические методы статистического анализа временных рядов / Н.Н. Труш. – Мн.: БГУ, 1999. – 218 с.