Д.т.н,профессор, Айдосов А., д.т.н.,профессор, Айдосов Г.А.

Исследования условия формирования атмосферных циркуляций локальных областей под влиянием изменений термических и орографических характеристик поверхности;

Во многих численных моделях динамики атмосферы для нахождения температуры почвы используется уравнение теплового баланса. Теплофизические характеристики почвы разнообразны, в результате чего даже в небольших расстояниях температуры над различными типами почвы могут резко различаться и тем самым влиять на динамику атмосферы в нижних слоях. Кроме того, тепловой и влажностные режимы в системе почва – воздух из-за взаимной связи между собой воздействуют на формирование и развитие растений и тем самым влияют на окружающую среду.

Тепловой режим в почве может быть наиболее полном описан на основе совместного рассмотрения процессов молекулярной теплопроводности почве и турбулентной теплопроводности в области приземного слоя атмосферы. В рамках одномерной модели пограничного слоя эти работы использовались в работах [1].

Рассмотрим процессы теплообмена в почве с учетом термодинамического состояния почвенной среды совместно с пространственной моделью пограничного слоя атмосферы. Исходным для нахождения температуры на поверхности земли является уравнение теплового баланса. Для определения тепловых и влажностных характеристик почвы рассмотрим следующее уравнение:

. (1)

Здесь С – теплоемкость почвы, задаваемая по формуле:

, (2)

где: – объемное влагосодержание; а – насыщающая влага или пористость почвы; – теплоемкость сухого грунта для соответствующего почвенного типа i.

В уравнении (2) теплоемкость воздуха не учитывается из-за ее малости. Коэффициент теплопроводности определяются с помощью следующих эмпирических формул, полученных из аппроксимации эмпирических данных /1/:

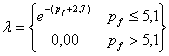, (3)

где ; – потенциал влаги в почве.

Здесь, как и в модели квазиоднородного приземного слоя, однородность почвы по горизонтали предполагается только в пределах одной ячейки сеточной области.

Отметим, что потенциал влаги соответствует верхнему горизонту воды и представляет собой работу против капиллярных сил и силы сопротивления, затрачиваемую на выделение воды из почвы. Из анализа экспериментальных данных получено, что связь между коэффициентом теплопроводности и потенциалом влаги слабо зависит от типа почвы.

Распределение количества влаги в почве определим из уравнения:

, (4)

Где , (5)

или , ; (6)

– поток влаги в почве; – гидравлическая проводимость; – плотность воды; z – вертикальная координата, определяемая как и в атмосфере; – коэффициент диффузии.

Следуя [1] определим переменные , , с помощью формул:

; (7)

; (8)

, (9)

где индексом “Н” отмечены значения соответствующих функции в условиях насыщения.

Одним из основных искомых параметров является относительная влажность или потенциал поверхности влаги. Связь между ними при равновесии представим в виде:

. (10)

Тогда удельная влажность на поверхности земли равна:

, (11)

а находится из формулы Магнуса.

Изменение влажности почвы влечет за собой изменение баланса радиации на поверхности земли из-за изменения альбедо подстилающей поверхности. С увеличением влажности альбедо уменьшается. Альбедо на поверхности почвы в первом приближении определим с помощью следующих эмпирических формул /1/:

- для чернозема: 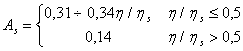; (12)

- для торфа: .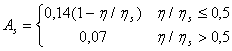

Общее альбедо подстилающей поверхности можно представить в виде:

, (13)

где учитывает зависимость зенитного угла солнца следующим образом:

, (14)

– зенитный угол солнца, , . Теперь с учетом уравнения теплового баланса необходимо согласовать поток влаги , идущий из почвы к поверхности земли, и турбулентный поток влаги, поступающий из почвы в атмосферу . Для этого достаточно потребовать, чтобы

. (15)

Система уравнений, описывающая динамику пограничного слоя атмосферы, является незамкнутой относительно величин , представляющих собой тензор вязких напряжений Рейнольдса. В настоящее время уже хорошо известно, что роль этих напряжений в динамике осредненного течения очень велика и пренебречь ими никак нельзя.

При самых ранних попытках решить систему уравнений гидротермодинамики турбулентные напряжения представлялись по аналогии с вязкими напряжениями в ньютоновской жидкости, только коэффициент пропорциональности перед градиентом скорости задавался большим и назывался коэффициентом турбулентного обмена или турбулентной вязкости:

, . (16)

В ранних работах, начиная с работы Экмана [1], уравнения решались с постоянными или как-либо априорно заданными коэффициентами турбулентного обмена. Решение системы уравнений гидродинамики при показывает, что оно не согласуется с некоторыми физически ясными свойствами интересующего нас течения, даже если толщину пограничного слоя рассматривать как заданный внешний параметр. Недостаток решения заключается в том, что из него следует пропорциональность сдвига ветра сдвигу скорости геострафического ветра при сколь угодно больших значениях .

Следующим этапом явились исследования Е.Н. Блиновой и И.А. Кибеля, М.Н. Юдина [1], в которых предложено выражать некоторые характеристики профиля коэффициенты турбулентного обмена через характеристики профиля средней скорости.

Далее А.С. Монин предложил для замыкания использовать уравнения баланса турбулентной энергии, и вытекающие из гипотезы приближенного подобия Колмогорова некоторые соотношения.

Суть моделей, основанных на замыкании второго порядка состоит в том, что вторые моменты, а именно напряжения Рейнольдса и потоки скалярных субстанции не апроксимируются посредством приближения турбулентной диффузии, а сохраняются как неизвестные параметры. Для замыкания задачи вводятся уравнения вторых моментов. Моменты из третьего порядка, которые появляются в уравнениях, апроксимируются на основании некоторых предположений подобия.

В данной работе, следуя [1], симметричный тензор напряжения , представим в виде функции, зависящей от тензора деформации среднего движения следующим образом:

, i, j=1, 2, 3, (17)

где 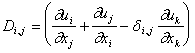. (18)

Поток тепла определим по формуле:

, j=1, 2, 3, (19)

где – параметры кинематической вязкости и диффузии.

Для определения пространственно-временных изменений параметра будем пользоваться формулировкой схемы замыкания:

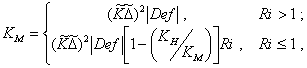, (20)

где , – объем элементной расчетной ячейки сеточной области; – числовая константа. Деформацию Def определим по формуле:

. (21)

Число Ричардсона Ri представим в следующем виде /1/:

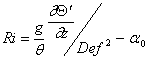, (22)

где ,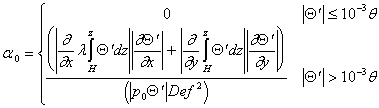

дополнительное слагаемое имеет стабилизирующий характер. Поскольку при наличии сильной орографической и термической неоднородности могут возникнуть большие температурные градиенты, введение параметра способствует погашению мелкомасштабных колебательных процессов. В численных расчетах значения безразмерной константы брались из интервала 0,2-0,4 .

При проведении численных расчетов в квазистатистическом приближении применяется несколько упрощенное представление турбулентных слагаемых в виде:

, , ;, ; , , , i=1, 2, , (23)

где коэффициенты вертикального турбулентного обмена определяются из уравнения баланса энергии турбулентности. Такое упрощение имеет смысл, поскольку в нижних слоях атмосферы одним из существенных факторов, влияющих на турбулентную структуру пограничного слоя атмосферы, являются вертикальные градиенты скорости ветра и температуры, которые на 1-2 порядка превосходят горизонтальные градиенты.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Айдосов А.А., Айдосов Г.А., Данаев Н.Т.,Аажиева Г. Математическое моделирование распространение вредных веществ в природной среде и методы оценки влияния нефтегазодобывающенй отрасли на экологическую обстановку региона. - Алматы: Изд-во «Қазақ университеті”, 2012.- 485 с.