ОЦЕНКА АППРОКСИМАЦИИ

НЕЛИНЕЙНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ ЛИНЕЙНЫМИ

¹Будылина Е.А., ²Гарькина И.А., ²Данилов А.М.

¹Московский государственный машиностроительный университет

²Пензенский государственный университет архитектуры и строительства

Трудности исследования нелинейных систем и процессов общеизвестны. Преодолевают их различного рода ухищрениями, а чаще всего используется аппроксимация более простыми объектами. В приложениях реальные сложные нелинейные системы и их математические модели заменяют линейными без соответствующих оценок. Иногда погрешности при такой замене столь значительны, что не только количественные характеристики, но даже качественное поведение реальной и аппроксимирующей систем является не адекватной.

Так, рассмотрим нелинейную систему

	(1)
,	(2)

здесь соответственно определяют траекторию объекта управления и управляющее воздействие.

Одновременно рассмотрим также систему

	(3)
,	(4)

где A, B – некоторые постоянные матрицы, - функция, определяемая условиями аппроксимации.

Если правая часть системы (1) является почти линейной по , а по меняется мало (система почти стационарна), то можно ожидать близость движения указанных двух систем. На мысль о такой линейной аппроксимации наводит также теоремы о непрерывной зависимости решений системы от параметров и возможности линейной аппроксимации непрерывных функций. Однако эти теоремы обосновывают лишь локальную аппроксимацию (на этом основаны и многие достаточно надежные численные методы решения дифференциальных уравнений), в частности, непрерывную функцию можно аппроксимировать линейной лишь в достаточно малой (зависит от требуемой точности) окрестности. Насколько существенными могут быть погрешности при глобальной аппроксимации, проиллюстрируем на примере системы второго порядка (с увеличением размерности погрешности могут значительно возрасти).

Решение задачи (3)-(4) в интегральном виде:

,

где - фундаментальная матрица решения системы

, .

Столбцы матрицы есть векторы вида

,

где - собственные числа матрицы A, - натуральные числа, не превосходящие кратности соответствующих чисел .

О погрешности между решениями задач (1) - (2) и (3) - (4) можно судить по изменению характеристических чисел в зависимости от изменения коэффициентов матрицы A (при глобальной аппроксимации матрица A определяется не однозначно правой частью системы (1)).

Проследим изменения собственных чисел матрицы в зависимости от изменения коэффициентов .

Собственные числа и определятся из уравнения (,). Изменим числа и , приняв и ( может быть как действительным, так и комплексным). Тогда и будут собственными числами некоторой новой матрицы , для которой в силу справедливо:

,	(5)
.	(6)

Из (5) и (6) следует, что, если мало, то матрицы и будут почти совпадать, но их собственные числа (определяют поведение решений) будут существенно отличаться. Так, если

, ,

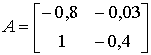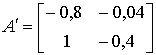то ,; ,. Как видим, матрицы и отличаются лишь одним коэффициентом (); их собственные числа отличаются по модулю на 0,1. Общие решения однородных систем с матрицей и отличаются по структуре и соответственно имеют вид

,

.

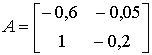Более того, изменение коэффициента на ту же величину 0,01 в системе с матрицей превращает колебательную систему в апериодическую.

Рассмотренная оценка корректности и точности линеаризации нелинейных уравнений движения объекта использовалась при разработке эргатической системы с высокоавтоматизированной системой автоматического управления.

Литература

1. Гарькина И.А., Данилов А.М., Домке Э.Р. Промышленные приложения системных методологий, теорий идентификации и управления / Вестник МАДИ. – 2009. – № 2(17). – С.77-82.

2. Гарькина И.А., Данилов А.М. Управление в сложных технических системах: методологические принципы управления / Региональная архитектура и строительство, №1 (12) , 2012, С.39-43.