Математика/5.
Математическое моделирование
Д.ф.-м.н. Соловьев С.В., К.т.н. Гринкруг Л.С.1
Тихоокеанский государственный университет, Россия
1. Приамурский государственный университет, Россия
Моделирование теплообмена и магнитной
гидродинамики в жидком ядре Земли
Современная теория геомагнитного поля
предполагает, что в жидком ядре Земли происходит непрерывное перемещение
вещества. В настоящее время не вызывает сомнений, что тепловая или
гравитационная конвекция в земном ядре является именно той причиной, которая
приводит к созданию геомагнитного поля. Теория геомагнитного поля получила
название гидромагнитного динамо (ГД) по аналогии с действием обычной
динамо-машины с самовозбуждением. Математическая трактовка теории вихревого
движения в ядре и возникновения в нем индукционных токов чрезвычайно затруднена
и в общем виде до сих пор не получила своего решения [1], так как решение
уравнений магнитной гидродинамики сопряжено с большими трудностями. Поэтому
теория ГД, в основном, развивается путем исследования кинематических моделей, в
которых скорость движения жидкости считается заданной, а определяется только
магнитное поле.
В
данной работе, в отличие от кинематических моделей гидромагнитного динамо, рассматривается конвективный теплообмен
электропроводящей жидкости в сферическом слое, моделирующем жидкое ядро Земли.
Исследовано влияние безразмерных критериев подобия на структуру течения и
теплообмен жидкости в сферической прослойке. Рассматриваются совместно уравнения
энергии - с учетом внутренних
источников тепла и джоулевой диссипации; движения - с учетом магнитных, вязких и подъемных сил; индукции
и неразрывности для скорости и магнитной индукции. Используется приближение
Буссинеска. Ускорение свободного падения направлено к центру ядра.
Математическая постановка задачи в безразмерной форме описывается
системой уравнений:
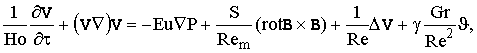 (1)
(1)
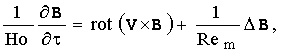
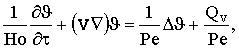 (2)
(2)
![]()
![]() (3)
(3)
Постоянная величина J в (1), определяющая джоулеву диссипацию, принимает различные значения в зависимости
от типа граничных условий (ГУ) для температуры. Задача решалась в переменных
температура-вихрь-функция тока.
Для температуры задавались следующие
граничные условия:
1. Температуры на Г1,2 : ![]() ;
;
2. Подвод тепла на Г1 и задание
температуры на Г2:
![]() ;
;
3. Задание температуры на Г1 и
теплового потока на Г2:
![]() («+» - подвод тепла; «-» - отвод тепла).
(«+» - подвод тепла; «-» - отвод тепла).
 .
. 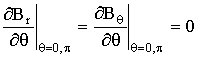 ,
, ![]() ,
,
![]() .
.
Для решения задачи
использовался метод конечных элементов. Для аппроксимации рассчитываемых полей
применялись билинейные конечные элементы. Дискретный аналог системы
дифференциальных уравнений был получен с применением метода взвешенных невязок.
Полученная система алгебраических уравнений решалась методом Зейделя с применением
нижней релаксации. По времени использовалась неявная схема.
На рис. 1-4 приведены результаты
стационарных расчетов для граничных температурных условий I рода полей температуры, функции тока, вихря,
радиальной и меридиональной составляющей магнитной индукции; локальные числа
Нуссельта.
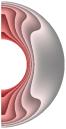
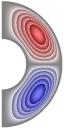
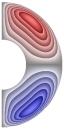
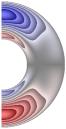

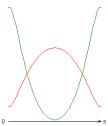 Рис. 1 ( J= Qv =0
)
Рис. 1 ( J= Qv =0
)
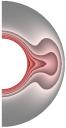
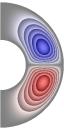
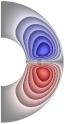
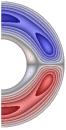

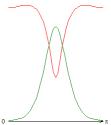 Рис. 2 (J≠0, Qv =0)
Рис. 2 (J≠0, Qv =0)
Gr = 103;
Re = 10 (Gr/Re2 = 10); S = 10-5; Rem = 1; Pe = 10; r2/r1 = 2,5.
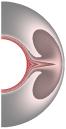
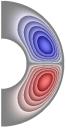
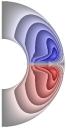
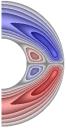
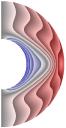
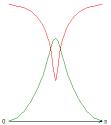 Рис. 3 (J= Qv =0)
Рис. 3 (J= Qv =0)

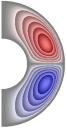
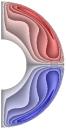
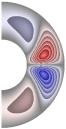
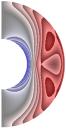
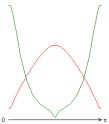 Рис. 4 (J≠0, Qv =0)
Рис. 4 (J≠0, Qv =0)
Gr = 104;
Re = 10; Gr/Re2 = 102; S = 10-5; Rem
= 1; Pe = 10
По предложенной математической модели были
получены результаты, анализ которых
позволил сделать следующие выводы:
- конвекция оказывает значительное влияние на магнитное
поле ядра Земли;
- учет джоулевой диссипации приводит к изменению
направления движения жидкости в
конвективных ячейках на противоположное (магнитные
полюса Земли изменяют свое местоположение на противоположное), что приводит к перестройке поля температуры в
ядре. Аналогичный результат был отмечен в работе [1];
- изменение внутреннего источника тепла на сток также
приводит к изменению направления движения
жидкости в конвективных ячейках на противоположное.
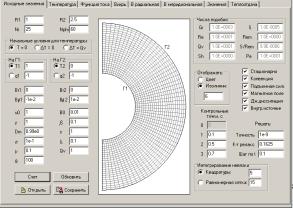
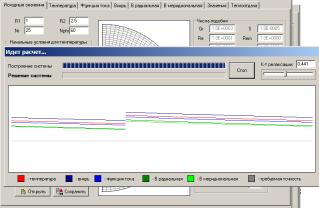
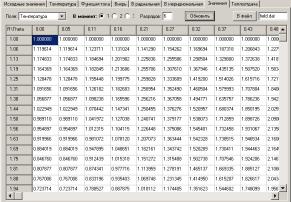
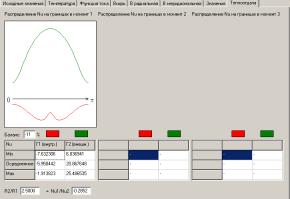
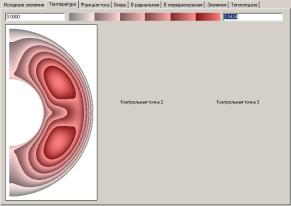
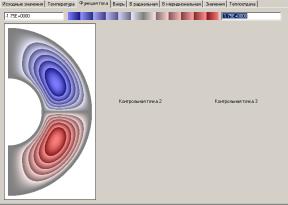
- создан ППП, экранные
формы которого приведены ниже
Литература
1.Краузе Ф., Рэдлер К.-Х. Магнитная гидродинамика
средних полей и теория динамо /Пер. с англ. А. Г. Муслимова, Н. А. Силантьева;
под ред. А. З. Доминова. - М.: Мир, 1984. - 314 с.