ЛИНГВОМАТЕМАТИЧЕСКАЯ МОДЕЛЬ

ДЛЯ АНАЛИЗА СТРУКТУРЫ КАЗАХСКОГО ТЕКСТА

Кажикенова С.Ш., Мазиева К.

Мы предлагаем идеальную лингвоматематическую модель для анализа структуры текста. Она построена на основе фундаментального закона сохранения суммы информации и энтропии с применением формулы Шеннона [1-4]. При общей характеристике энтропийно-информационного (энтропия - мера беспорядка, а информация – мера снятия беспорядка) анализа текстов мы использовали статистическую формулу Шеннона для определения совершенства, гармонии текста:

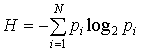, (1)

где р_i – вероятность обнаружения какого-либо однородного элемента системы в их множестве ; , .

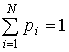До опубликования созданной Шенноном теории Хартли предложил определять количество максимальной энтропии по формуле

.

Казахский алфавит содержит 43 буквы (42 буквы, 1 пробел), то согласно этому результату

бит.

- энтропия опыта, заключающегося в приеме одной буквы казахского текста (информация, содержащаяся в одной букве), при условии, что все буквы считаются одинаково вероятными.

В качестве примера был рассмотрен текст, связанный с казахской музыкой. Текст содержит знаков с пробелами –500, без пробелов –431

Ориентировочные значения частот отдельных букв казахского языка представлены в таблице 1и 2 (тире здесь обозначает пробел между словами). В таблице 1 буквы расположены в алфавитном порядке, таблице 2 по мере убывания относительных частот.

Таблица 1

	Буква	Относительная частота	№	Буква	Относительная частота
1.	пробел	0,138	23	п	0,008
2.	а	0,112	24	р	0,052
3.	ә	0,01	25	с	0,026
4.	б	0,018	26	т	0,042
5.	в	0	27	у	0,022
6.	г	0,004	28	ұ	0,002
7.	ғ	0,008	29	ү	0,008
8.	д	0,034	30	ф	0
9.	е	0,042	31	х	0,01
10	ё	0	32	һ	0
11	ж	0,014	33	ц	0
12	з	0,028	34	ч	0
13	и	0,004	35	ш	0,006
14	й	0,018	36	щ	0
15	к	0,036	37	ъ	0
16	қ	0,018	38	ы	0,124
17	л	0,036	39	і	0,032
18	м	0,05	40	ь	0
19	н	0,044	41	э	0
20	ң	0,026	42	ю	0
21	о	0,014	43	я	0,004
22	ө	0,01

Таблица 2

буква относ.частота	__ 0,138	ы 0,124	а 0,112	р 0,052	м 0,05	н 0,044	е 0,042	т 0,042
буква относ.частота	к 0,036	л 0,036	д 0,034	і 0,032	з 0,028	ң 0,026	с 0,026	у 0,022
буква относ.частота	б 0,018	й 0,018	қ 0,018	ж 0,014	о 0,014	ә 0,01	ө 0,01	х 0,01
буква относ.частота	ғ 0,008	п 0,008	ү 0,008	ш 0,006	г 0,004	и 0,004	я 0,004	ұ 0,002

Приравняв эти частоты вероятностям появления соответствующих букв, получим на основании информационной энтропии Шеннона формулу для расчета максимального значения энтропии текста при учете одной буквы казахского текста:

:

Ориентировочные значения частот двухбуквенных сочетаний казахского языка представлены в таблице 3 (тире здесь обозначает пробел между словами). В таблице 3 буквы расположены по мере убывания относительных частот.

Таблица 3

сочетание относ.частота	ы - 0,032	- м 0,022	ры 0,022	ың 0,020	ң - 0,020	му 0,020	уз 0,020	зы 0,020
сочетание относ.частота	ык 0,020	ка 0,020	ты 0,018	- т 0,018	та 0,018	н - 0,018	і - 0,016	а - 0,016
сочетание относ.частота	ыр 0,016	лы 0,016	- б 0,014	ар 0,014	- ж 0,014	мы 0,014	ал 0,012	ық 0,012
сочетание относ.частота	ас 0,012	сы 0,012	ба 0,012	- к 0,012	ам 0,012	ен 0,012	ер 0,012	- х 0,001
сочетание относ.частота	ха 0,01	да 0,01	рі 0,01	- о 0,01	ын 0,01	нд 0,01	ан 0,01	де 0,001
сочетание относ.частота	р - 0,008	қт 0,008	- ә 0,008	ән 0,008	ді 0,008	- д 0,008	п - 0,008	ай 0,008
сочетание относ.частота	ны 0,008	ла 0,008	ме 0,008	жы 0,008	ні 0,006	із 0,006	жа 0,006	кө 0,006
сочетание относ.частота	- а 0,006	ды 0,006	кү 0,006	үй 0,006	йл 0,006	ле 0,006	ол 0,006	ыл 0,006
сочетание относ.частота	- с 0,006	рм 0,006	қ - 0,006	ор 0,004	йт 0,004	ег 0,004	ге 0,004	ім 0,004
сочетание относ.частота	мі 0,004	ат 0,004	з - 0,004	зд 0,004	ағ 0,004	ға 0,004	л - 0,004	- ө 0,004
сочетание относ.частота	се 0,004	ед 0,004	аң 0,004	ңа 0,004	ып 0,004	ей 0,004	рл 0,004	аш 0,004
сочетание относ.частота	- е 0,004	йд 0,004	лм 0,004	ма 0,004	әр 0,002	бі 0,002	ің 0,002	ақ 0,002
сочетание относ.частота	қс 0,002	өр 0,002	іп 0,002	ңд 0,002	өп 0,002	ым 0,002	ыз 0,002	өт 0,002
сочетание относ.частота	тк 0,002	ке 0,002	са 0,002	йы 0,002	өс 0,002	е- 0,002	тү 0,002	аб 0,002
сочетание относ.частота	үс 0,002	өб 0,002	бе 0,002	йе 0,002	шт 0,002	си 0,002	ия 0,002	яқ 0,002
сочетание относ.частота	еш 0,002	шқ 0,002	қа 0,002	ша 0,002	ес 0,002	ск 0,002	кі 0,002	ір 0,002
сочетание относ.частота	со 0,002	то 0,002	ығ 0,002	ғы 0,002	от 0,002	ра 0,002	ад 0,002	- я 0,002
сочетание относ.частота	яғ 0,002	ғн 0,002	ни 0,002	и - 0,002	он 0,002	ст 0,002	ау 0,002	у - 0,002
сочетание относ.частота	бұ 0,002	ұл 0,002

Далее подсчитаем условную энтропию опыта , состоящего в определении одной буквы казахского текста при условии, что нам известен исход опыта , состоящего в определении предшествующей буквы того же текста. Согласно вышесказанному определяется следующей формулой:

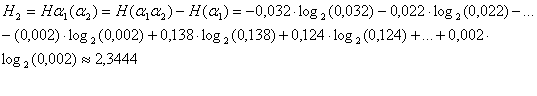
Аналогично этому можно определить и энтропию .

Приравняв эти частоты вероятностям появления соответствующих трехбуквенных сочетаний, что находит отражение в разности , получим для энтропии трех букв казахского текста приближенное значение:

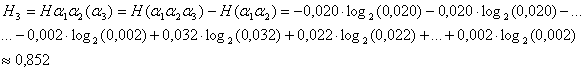
для расчета максимального значения энтропии текста при учете четырех букв казахского текста:

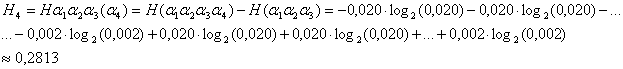
при учете пяти букв казахского текста составляет приближенное значение:

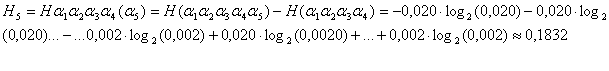
Согласно сказанному выше, для определения условной энтропии посчитали число всех шестибуквенных сочетаний в данном тексте. Посчитали шестибуквенные сочетания и применили формулу классического определения вероятности

,

где п - число всех 6-ти буквенных сочетаний,

m – число сочетании, например, музыка.

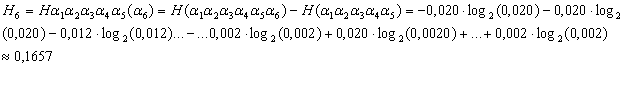
В результате были получены следующие значения (в битах):

4,3598 2,3444 0,852 0,2813 0,1882 0,1657.

Таким образом, полный анализ показывает, что план построения сложной информационной системы может формироваться только на верхних иерархических уровнях и оттуда спускаться на нижележащие уровни, задавая на них тот или иной порядок чередования элементов.

Используемый теорией информации статистический метод учета межбуквенных корреляций в литературных текстах обоих языков зависит от смыслового контекста и одна, и две, и три буквы и т.д. могут быть в одних случаях самостоятельным словом, а в других - входить в состав других слов.

Очевидно, что рассматриваемые сочетания букв относятся к различным иерархическим уровням текста, однако подобное разграничение уровней может осуществляться только по смыслу, который заключает в себе анализируемый текст.

Литература

1 Кажикенова С.Ш., Оспанова Б.Р. Информационно-энтропийный анализ структуры текста // Караганда: Изд-во КарГТУ, 2012. – 251с.

2 Кажикенова С.Ш., Оспанова Б.Р. К вопрос у о формировании концептуальной системы целевого языка в структуре коммуникативной компетенции // Язык и культура. – Томск, 2012.- №3. – С. 111-121.

3 Кажикенова С.Ш., Оспанова Б.Р. О некоторых аспектах языковой модели в теории информации // Международный журнал экспериментального образования. – М., 2012. - №8. – С. 115-120.

4 Кажикенова С.Ш., Оспанова Б.Р. Лингвосинергетический подход к исследованию текста как самоорганизующегося объекта // Хаос и структуры в нелинейных системах. Материалы междунар. науч.-практ. конф.(18-20 июня)/КарГУ. – Караганда: Изд-во КарГУ, 2012. – С.546-550