Наметбаев
Г.Ш., Чернявская Н.П.,Туленбаев Ж.С.
Таразский
государственный университет им.М.Х.Дулати, Казахстан
ПРЕОБРАЗОВАНИЕ
АНАЛОГОВЫХ СИГНАЛОВ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ НА ПРИМЕРЕ СЕЙСМОГРАММ.
Значительная группа измерительных
устройств преобразует измеряемую величину в пропорциональный аналоговый чаще
всего электрический сигнал. При
анализе, исследовании или проектировании возникает необходимость
математического описания подобных сигналов в виде функций. С подобной задачей
авторы столкнулись при экспериментальном исследовании различных видов
фундаментов на сейсмостойкость. Для определения параметров колебаний
исследуемых фундаментов был использован гальванометрический способ регистрации.
Этот способ, благодаря высокой точности и простоте осуществления многоканальной
записи, широко применяется в экспериментальной практике. В качестве первичного
преобразователя использованы сейсмоприемники
C5G в комплекте с гальванометрами МО02 (смещение) и сейсмоприники 0СП-2М
в комплекте с гальванометрами МОХ7 (ускорение).
Подбор гальванометров для измерения параметров
колебаний был осуществлен согласно техническим характеристикам сейсмоприборов, запись
осуществлялась на светолучевых осциллографах Н041 и Н044.2.
Для ступенчатого снижения величины электрического сигнала
между сейсмоприемниками и гальванометрами были подключены шунтовые коробки Щ-1.
Все приборы стандартные заводского изготовления. Получение достоверных результатов
измерений связано с построением амплитудно-частотных характеристик каналов
измерительного стенда. Аналитические методы построения их по паспортным
параметрам приборов весьма трудоемки. В связи с этим характеристики виброизмерительных
приборов стремятся определить экспериментально.
По результатам экспериментов были получены
сейсмограммы, примеры которых приведены на рис.1. В ходе дальнейших
исследовании, а именно определения оптимальных параметров исследуемых
фундаментов, возникла необходимость математического описания этих сейсмограмм.
Для этих целей был использован метод быстрого преобразования Фурье(БПФ).
Основная проблема, возникающая при практической реализации преобразования
Фурье, заключена в большом количестве вычислительных операций, пропорциональном
N2-колличеству дискретизации. Хотя еще задолго до появления компьютеров было
предложено несколько эффективных вычислительных схем, позволяющих существенно
сократить число вычислительных операций, настоящую революцию произвела
публикация в 1965 году статьи Кули (Cooly) и Тьюки (Tukey) c практическим
алгоритмом быстрого (число операций Nlog2N) вычисления 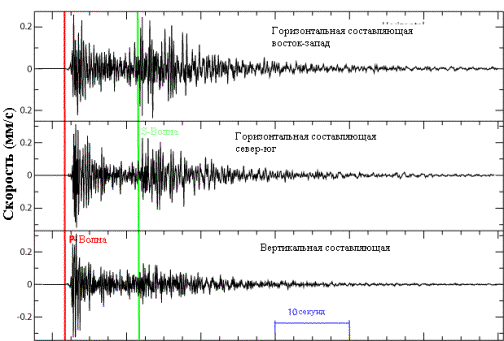
Рисунок 1. Сейсмограмма.
После этого было разработано множество вариантов,
усовершенствований и дополнений основной идеи, составивших класс алгоритмов,
известных под названием быстрого преобразования Фурье. Основная идея БПФ -
деление N-точечного ПФ на два и более ПФ меньшей длины, каждый из которых можно
вычислить отдельно, а затем линейно просуммировать с остальными, с тем чтобы
получить ПФ исходной N-точечной последовательности.
Представим дискретное преобразование Фурье (ПФ) в виде
![]() , (1)
, (1)
где величина WN=exp(-j2/N) носит название
поворачивающего множителя (здесь и далее в этом разделе период выборки T=1).
Выделим из последовательности x[n] элементы с четными и нечетными номерами
![]() (2)
(2)
Но так
как![]() то
то
![]() .
Следовательно, (36) можно записать в виде
.
Следовательно, (36) можно записать в виде
![]() , (3)
, (3)
где
каждое из слагаемых является преобразованием длины N/2
![]() (4)
(4)
Заметим, что последовательность
(WN/2)nk периодична по k с периодом N/2. Поэтому, хотя номер k в
выражении (3) принимает значения от 0 до N-1, каждая из сумм вычисляется для
значений k от 0 до N/2-1. Можно оценить число комплексных операций умножения и
сложения, необходимых для вычисления преобразования Фурье в соответствии с
алгоритмом (3)-(4). Два N/2-точечных преобразования Фурье по формулам (4)
предполагают выполнение 2(N/2)2 умножений и приблизительно столько
же сложений. Объединение двух N/2-точечных преобразований по формуле (3)
требует еще N умножений и N сложений. Следовательно, для вычисления
преобразования Фурье для всех N значений k необходимо произвести по N+N2/2
умножений и сложений. В то же время прямое вычисление по формуле (1) требует по
N2 умножений и сложений. Уже при N>2 выполняется неравенство N+N2/2
< N2 и, таким образом,
вычисления по алгоритму (3)-(4) требуют меньшего числа математических операций
по сравнению с прямым вычислением преобразования Фурье по формуле (1). Так как
вычисление N-точечного преобразования Фурье через два N/2-точечных приводит к
экономии вычислительных операций, то каждое из N/2-точечных ДПФ следует
вычислять путем сведения их к N/4-точечным преобразованиям:
![]() ,
(5)
,
(5)
![]() (6)
(6)
При этом, вследствие периодичности последовательности WnkN/4
по k с периодом N/4, суммы (6) необходимо вычислять только для значений k от 0
до N/4-1. Поэтому расчет последовательности X[k] по формулам (3), (4) и (6)
требует, как нетрудно подсчитать, уже по 2N+N2/4 операций умножения
и сложения.
Следуя таким путем, объем вычислений X[k] можно все более и
более уменьшать. После m=log2N разложений приходим к двухточечным
преобразованиям Фурье вида
![]() (7)
(7)
где
"одноточечные преобразования" X1[k,p] представляют собой
просто отсчеты сигнала x[n]:
X1[k,q] = x[q]/N,
q=0,1,...,N-1. (8)
В
итоге можно записать алгоритм БПФ, получивший по понятным причинам название алгоритма с прореживанием по времени
:
X2[k,p] = (x[p] + Wk2x[p+N/2])
/ N,
где k=0,1,
p=0,1,...,N/2 -1;
X2N/M[k,p] =XN/M[k,p]
+ Wk2N/MXN/M[k,p+M/2],
где k=0,1,...,2N/M -1,
p=0,1,...,M/2 -1;
X[k] = XN[k]
=XN/2[k,0] + WkNXN/2[k,1], (9)
где
k=0,1,...,N-1
На каждом этапе вычислений
производится по N комплексных умножений и сложений. А так как число разложений
исходной последовательности на подпоследовательности половинной длины равно log2N,
то полное число операций умножения-сложения в алгоритме БПФ равно Nlog2N.
При больших N имеет место существенная экономия вычислительных операций по
сравнению с прямым вычислением ДПФ. Например, при N = 210 =
1024 число операций уменьшается в 117 раз.
Рассмотренный нами алгоритм БПФ с прореживанием по времени
основан на вычислении преобразования Фурье путем формирования
подпоследовательностей входной последовательности x[n]. Однако можно
использовать также разложение на подпоследовательности преобразования Фурье
X[k]. Алгоритм БПФ, основанный на этой процедуре, носит название алгоритма с
прореживанием по частоте.
Подробнее о быстром преобразовании Фурье можно прочитать, например, в [1,2].
Программная реализация БПФ есть практически во всех математических пакетах и
библиотеках. Между тем, опыт показывает, что, при всей своей простоте, метод
начинает вызывать некоторые вопросы, когда возникает необходимость не просто
посмотреть наличие дискреток в сигнале, но и выяснить их абсолютные значения,
т.е. нормализовать полученный результат. MATLAB позволяет
не связываться с ручным удалением ненужных объектов, однако, при работе с более
менее объемными массивами данных, имеет привычку капризничать и жаловаться на
недостаток памяти. Для освобождения памяти используется процедура clear с
указанием имени объекта, который необходимо удалить. [3] Использовав,
стандартную программу БПФ из пакета MATLAB мы получили функцию, представляющую
собой сумму синусоид и описывающую подобные сейсмограммы рис.1. Кроме того, мы
определили частоты наиболее энергонесущие, т.е. частоты наиболее
разрушительные.
1.
Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. М.:Мир,
1978.
2.
Марпл-мл. С.Л. Цифровой спектральный анализ и его приложения: Пер. с англ. -М.:
Мир, 1990.
3. http://psi-logic.narod.ru/fft/fft.htm