Л.Г. Поляков ¹, М.А. Гаврилов ², Е.М. Тишина ³

¹Кандидат технических наук, доцент, ²старший преподаватель, ³старший преподаватель, Пензенский Государственный Университет Архитектуры и Строительства, г. Пенза

МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ БЕЗОТКАЗНОСТИ СИСТЕМ ЗНАНИЙ, УМЕНИЙ И НАВЫКОВ

В данной статье рассматривается один из возможных математических подходов количественной оценки безотказности знаний специалистов. Основным принципом оценки является расчленение общей задачи на элементы решения и определения их количественных значений показателей безотказности (вероятность безотказности полученных знаний). Далее на основе этих значений, с использованием теории надежности, производится оценка системы знаний специалиста в целом. Кроме того, в статье приведены примеры использования предлагаемой математической методики применительно к начертательной геометрии.

Ключевые слова: математическое обеспечение, безотказность, надежность, знания, специалисты, начертательная геометрия.

Подготовка высококвалифицированных специалистов неразрывно связано с качеством их профессиональной подготовки, т.е. с надежностью обучения. Одним из составляющих свойств надежности обучения является безотказность применения полученных знаний, умений и навыков на практике [1]. Под безотказностью обучения предлагается понимать свойство процесса обучения, который позволяет непрерывно сохранять возможность использования полученных знаний, умений и навыков в течение некоторого (заданного) времени. (В дальнейшем под понятием сочетания «Знание, умение и навыки» будем использовать термин «Знание»).

Для всесторонней количественной оценки этого свойства обучения возникает необходимость рассмотрения процесса реализации полученных знаний (процесс решения задач), т.е. умение решение задач.

Решение любой задачи, в общем случае, представляет собой выполнение отдельных операций (шагов). Если введем понятие элемент решения, тогда решение задачи в целом есть система взаимодействия элементов. Под элементом решения следует понимать один шаг решения задачи, заключающийся в применении конкретной формулы, отдельной операции, использования отдельного навыка или умения, принятие промежуточного решения по принципу «да – нет» и т.п. Говоря другими словами, шаг это элементарное действие или этап в процессе решения задачи. Если элементарное действие это шаг решения задачи тогда совокупность элементов решение задачи в целом это система, а их соединение есть последовательность решения задачи.

Учитывая, определения элемент и система, то показатели безотказности можно подразделять на показатели безотказности элементов и показатели безотказности систем знаний, умений и навыков.

В данной статье рассматривается только показатели безотказности, применительно к системам знаний. Для дальнейших рассуждений введем понятия «Работоспособное состояние» и «Состояние отказа» уровня знаний испытуемого в текущий момент времени. Если под работоспособным состоянием системы понимать такое состояние уровня знаний испытуемого, при котором он может достичь положительного результата решения, то не возможность получения положительного решения будет являться состоянием отказа системы.

Для безотказности системы знаний предлагается использовать только один показатель[1, 2, 3, 4] - вероятность безотказности полученных знаний системы p_c(t) (ВБЗС). Расчет ВБЗС зависит от способа соединения элементов.

Различают три основных способа соединения элементов в системах:

a) последовательное (основное);

b) параллельное (кроме основного включает избыточные элементы);

c) смешанное соединение, т.е. часть элементов соединены последовательно, а часть параллельно.

Последовательное соединение. Оно еще называется основным (рис.1)

Рис.1. Последовательное соединение

В этом соединении нет резервных элементов. При таком соединении утрата знаний (отказ) хотя бы по одному элементу приводит к наступлению отказа всей системы, т.е. задача не может быть решена. Для определения ВБЗС, имеющей основное соединение элементов, существует мнемоническое правило: p_c(t) равна произведению вероятностей безотказности полученных знаний всех элементов p_i(t), т.е.

, (1)

где N – количество элементов в системе;

p_i(t) – вероятность безотказности полученных знаний по i-му элементу.

Формула (1) справедлива в том случае, когда отказы i – х элементов являются независимыми. Для зависимых отказов используются другие формулы. Вероятности не утраты знаний p_i(t) могут быть определены, согласно [2,3], по следующей статистической формуле

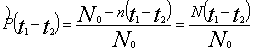, (2)

где

N₀ – число испытуемых до начала наблюдений;

t₁-t₂ – отрезок времени, в течении которого велись наблюдения;

n(t₁-t₂) – число испытуемых, утративших знания за время (t₁-t₂).

В некоторых случаях в место значения p_i(t) можно задаются интенсивностью утраты знаний составляющих элементов системы l_I. Учитывая, что

Λ_сt=, (3)

где Λ_сt - интенсивность отказа в положительном решении для системы в целом по истечению времени t.

Тогда

. (4)

Правая часть зависимости (20) определяется при разложении в ряд величины

. (5)

На практике желательно использовать только составляющие первого порядка, составляющие высших порядков на точность расчетов оказывают несущественное влияние. При этом зависимость 1 - Λ_сt можно использовать при условии, когда

Λ_сt≤0,2. (6)

Параллельное соединение. При параллельном соединении только один элемент является основным, все остальные – избыточные (резервные). В этом случае система откажет тогда, когда откажут и 1-й, и 2-й, и 3-й, и N-й элементы (рис.2).

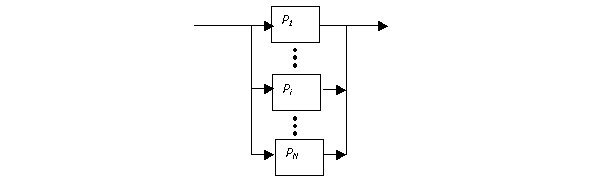
Рис.2. Параллельное соединение

Для параллельного постоянного соединения элементов существует мнемоническое правило: вероятность отказа системы Q_с(t) равна произведению вероятностей утраты знаний составляющих элементов q_i(t), т.е.

. (7)

В этом случае ВБЗС определяется по формуле

. (8)

Если для составляющих i-тых элементов заданы вероятности безотказности полученных знаний p_i(t), то зависимость (24) можно записать в следующем виде:

. (9)

Общая схема соединения элементов. На практике чаще всего встречается смешенное соединение элементов. Это соединение имеет две разновидности, упрощенный вид их приведен на рис.3.

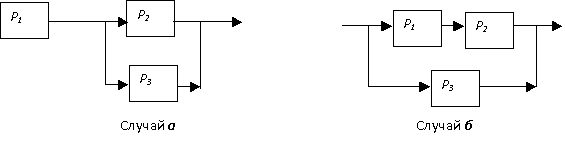
Рис.3. Смешенное соединение

На рис.3 для случая а схема имеет последовательно-параллельное соединение отдельных элементов. Элементы 2 и 3 соединены параллельно, а элемент 1 последовательно к ним. В этом случае в основу берется основное соединение. Величина p_c(t) всей системы определяется по формуле

, (10)

где Р₁ – вероятность безотказности полученных знаний 1-го элемента;

Р_2,3 – вероятность безотказности полученных знаний подсистемы, состоящей из элементов 2 и 3.

Подсистема элементов 2 и 3 определяется на основе параллельного соединения элементов

, (11)

где Q_2,3 – вероятность утраты знаний подсистемы элементов 2 и 3.

Теперь, подставляя (26) в формулу (27) окончательно получим:

. (12)

Если вместо исходных величин Р₁, Р₂, Р₃ будут заданы интенсивности утраты знаний l₁, l₂, l₃ и время использования системы t, то величину p_c(t) этой системы можно определить также по формуле (18). Вместо Р_i здесь надо подставить значение P_i(t)=1-l_i(t), полученное по формуле (20). Тогда

. (13)

Общая схема имеет параллельное соединение одной или нескольких подсистем или элементов. На рис.3, случай б подсистема (1, 2) параллельно соединена с элементом 3. В этом случае за основу расчета берется параллельное соединение (см рис.2). Для случая б (рис.3)

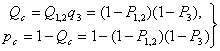, (14)

где Р_1,2 – вероятность безотказности полученных знаний подсистемы (1, 2), которая определяется по формуле (1)

. (15)

Теперь окончательно формула (14) будет иметь вид:

. (16)

Если в качестве исходных данных будут заданы интенсивности утраты знаний системы l₁, l₂, l₃ и время использования системы t, то формула (16) запишется в следующем виде:

. (17)

Рассмотрим пример для предмета «Начертательная геометрия». В состав изучения этого предмета входят следующие темы: тока; прямая; плоскость; позиционные задачи; метрические задачи.

Через год после изучения данной дисциплины в результате экспертного опроса были выявлены следующие результаты вероятностей безотказности полученных знаний, умений и навыков по указанным темам [2]. Некоторые результаты этого опроса приведены в табл.

Таблица

Результаты усвоения материала по начертательной геометрии

(через год после изучения курса)

№ п/п	Наименование темы	Вероятность безотказности полученных знаний Рi
1	Точка на эпюре Монжа	0,92
2	Прямая на эпюре Монжа	0,90
3	Прямые частного положения	0,89
4	Определение натуральной величины отрезка способом прямоугольного треугольника	0,64
5	Определение натуральной величины отрезка способом замены плоскостей проекций	0,69
6	Определение натуральной величины отрезка способом вращения вокруг проецирующей прямой	0,59

Пример № 1. Пусть задана задача. Построить Эпюр фронтали, проходящей через точку А(40;50;30) под углом 45⁰ к плоскости проекций П₁. Определить вероятность правильного решения задачи студентами через год после изучения курса «Начертательная геометрия».

Решение. Чтобы решить задачу по построению фронтали необходимо знать темы: точка на эпюре Монжа; прямая на эпюре Монжа; прямые частного положения. Следовательно, имеется три элемента: элемент 1 – точка на эпюре Монжа; элемент 2 – прямая на эпюре Монжа; элемент 3 – прямые частного положения. Не знание одной из этих тем приводит к отрицательному результату решения. Значит, элементы в системе соединены между собой последовательно (рис.1) и описывается формулой (17). Из табл. имеем Р₁=0,92, Р₂=0,90, Р₃=0,89. Теперь вероятность правильности решения задачи составит

.

Пример №2. Пусть задана задача. По заданным точкам А(10;20;.30) и В(90;100;80) найти натуральную величину отрезка [AB]. Рассчитать вероятность безотказного решения задачи студентами через год после изучения курса «Начертательная геометрия».

Решение. Для решения задачи вначале необходимо построить отрезок [AB], а затем определить его натуральную величину. Для определение натуральной величины отрезка можно использовать следующие способы: способ прямоугольного треугольника определения натуральной величины отрезка; метод замены плоскостей проекций; метод вращения вокруг проецирующей прямой. Следовательно, система состоит из пяти элементов: элемент 1 – точка на эпюре Монжа; элемент 2 – прямая на эпюре Монжа; элемент 3 – определение натуральной величины отрезка способом прямоугольного треугольника; элемент 4 – определение натуральной величины отрезка способом замены плоскостей проекций; элемент 5 – определение натуральной величины отрезка способом вращения вокруг проецирующей прямой. Элементы 1, 2 и подсистема элементов 3, 4, 5 соединены последовательно. Подсистема элементов 3, 4 и 5 имеет параллельное соединение. Общая схема имеет смешенный вид рис. 3 (случай б). Из табл. имеем Р₁=0,92, Р₂=0,90, Р₃=0,64, Р₄=0,69, Р₅=0,59. Теперь используя зависимости (8) и (16), применительно к данной системе, вероятность правильности решения задачи составит

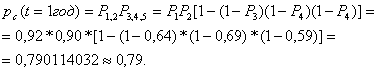
Таким образом, на основе математические зависимостей (1 – 17), с использованием статистических данных по усвоению отдельных элементов знаний, умений и навыков, можно количественно оценить эффективность любой системы обучения специалистов. Кроме того, появляется возможность управления самим процессом обучения исходя из условий изменения требований предъявляемым к специалистам.

Список используемой литературы

1. Л.Г. Поляков, Е.Е. Петрикова. К вопросу о безотказности использования полученных знаний. Сборник статей 1 городской межвузовской научно-практической конференции. Молодежь ХХI столетия: вопросы образования, воспитания и социализации. - Пенза: ПГПУ, 2010

2 Л.Г. Поляков, Е.Е. Петрикова. Показатели безотказности системы полученных знаний. Сборник статей международной научно-методической конференции. Инновационные технологии организации обучения в техническом ВУЗе. Часть 1. – Пенза: ПГУАС, 2010

3. Надежность технических систем: Справочник. Ю. К. Беляев, В. А. Богатырев, В. В. Болотин и др.; Под ред. И. А. Ушакова. - М.: Радио и связь, 1985. - 608 с, ил.

4. Справочник по расчету надежности машин на стадии проектирования /Б.Ф. Хазов, Б.А. Дедусев. -. М.: Машиностроение, 1986.