Педагогические науки. Проблемы подготовки специалистов.

Небратенко О.В., Спица А.И.

Харьковский национальный автомобильно-дорожный университет

ПРИМЕНЕНИЕ МЕТОДА МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ

К ВЫЧИСЛЕНИЮ СУММ И ПРОИЗВЕДЕНИЙ

На разных этапах развития науки преобладали различные стороны познавательных процессов, вследствие чего на первый план исследований выдвигались соответствующие типы умозаключений – логических выводов. Менялись и принципы описания умозаключения, и уровень строгости анализа.

При исследовании умозаключений уже давно обратили внимание на два принципиально различных направления мышления: дедуктивное, когда мысль движется от общего – к менее общему, частному, единичному, и индуктивное, при котором движение мысли происходит от менее общего, частного, единичного – к более общему. Соответственно, выводы, стали называть дедуктивными и индуктивными.

«Индукция, «наведение» на мысль, на догадку, на гипотезу, играет в математике очень большую, но чисто эвристическую роль: позволяет догадываться о том, каким, по всей видимости, должно быть решение». [1]. В качестве доказательства метод индукции в математике не применяется. Но в области натуральных чисел многие утверждения доказываются особым методом рассуждений, представляющим синтез дедуктивного и индуктивного, называемым методом математической индукции.

В работе приведены некоторые примеры применения метода математической индукции в теории числовых рядов в математическом анализе. Рассмотрим применение метода математической индукции к решению задач, связанных с вычислением сумм и произведений. Суть метода состоит в доказательстве, что некоторое утверждение (формула) справедлива для любых целых n. Для доказательства следует выполнить два действия: убедиться, что утверждение справедливо при n=1; предположить, что утверждение справедливо при n=k, и доказать, что оно остается справедливым при n=k+1. Если это удалось выполнить, то утверждение справедливо для любых n.

Вывод формул для n-частичных сумм числовых рядов

1) Пусть

геометрическая прогрессия со знаменателем q. n - частичная сумма геометрической прогрессии равна

.

Замечаем, что

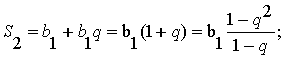
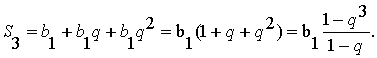
Предполагаем, что 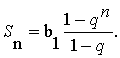(1)

Убедимся, что утверждение справедливо при n=1. Пусть n=1, тогда , т.е. формула справедлива при n=1.
Предположим, что равенство 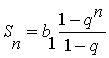справедливо при n=k, т.е. верно 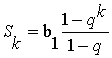. Находим частичную сумму

.
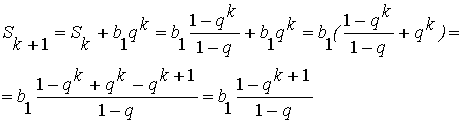Получили, что при n=k+1 равенство (1) выполнено. Так как утверждение справедливо при n=1 и позволяет перейти от n=k к n=k+1, то формула (1) справедлива при всех целых n ()

.

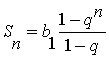2) Зададим числовой ряд . Вычислим n-частичную сумму этого ряда и докажем, что 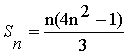(2)

Формула (2) справедлива при n=1 ().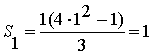

Допустим, что равенство (2) верно и при n=k, т.е.

.

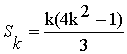Равенство (2) рассмотрим при n=k+1

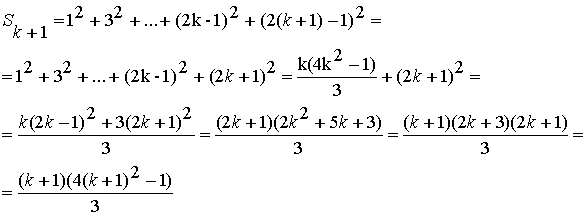. Так как равенство справедливо при n=1 и позволяет переходить от n=k к

n=k+1, то утверждение (2) справедливо.

3) Зададим числовой ряд . Вычислим n-частичную сумму этого ряда и докажем, что . (3)

.

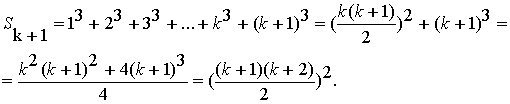
Видим, что равенство (3) справедливо при n=k+1. Поскольку утверждение выполнено при n=1 и позволяет переходить от k к k+1, то формула (3) справедлива при всех .

Докажем, что произведение равно

, . (4)

Убедимся, что формула (4) верна при n=2

. Действительно, .

Полагаем, что . Вычислим :

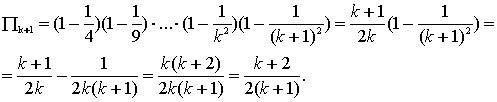
Получили, что утверждение (4) при n=k+1 справедливо. Так как утверждение (4) справедливо при n=2 и допустим переход от k к k+1, то утверждение справедливо при всех целых .

Метод математической индукции, как синтез дедуктивного и индуктивного методов, является чрезвычайно плодотворным методом доказательств в области натуральных чисел. «Метод математической индукции позволяет в поисках общего закона испытывать возникающие при этом гипотезы, отбрасывая ложные и утверждать истинные».[1]. В результате развивается логическое мышление, формируется умение обобщать и анализировать. Поэтому метод математической индукции должен быть всегда в «багаже» учащихся, ориентированных на обучение деятельности по приобретению новых знаний.

Литература

[1] – Соминский И.С. О математической индукции / И.С. Соминский, Л.И.Головина, И.М. Яглом // М: Изд-во «Наука». – 1967. – 144 с.