Физика /3. Физика плазмы и плазменная техника

Г.С. Калюжный, Е.Ю. Лыштван, Н.В. Солодухин

Восточноукраинский национальный университет им. Владимира Даля

ДИНАМИКА РАЗВИТИЯ ВОЗМУЩЕНИЙ

ТОКА ДУГИ ПЛАЗМОТРОНА

ВВЕДЕНИЕ

Проблема устойчивости системы источник питания – дуга плазмотрона по отношению к малым возмущениям тока рассматривалась во многих работах [1,2]. При этом само возмущение предполагалось уже сформировавшимся. В настоящей работе рассматривается динамика развития возмущения тока дуги, вызванного малыми изменениями напряжения источника питания и скорости расхода продуваемого сквозь плазмотрон газа.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Рассмотрим математическую модель возмущений тока дуги для простейшей схемы питания плазмотрона, показанной на рисунке 1.

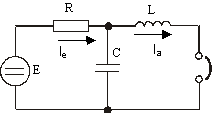
Рисунок 1 – Схема питания плазмотрона

Внутреннее сопротивление источника питания будем считать равным нулю. Из уравнений Кирхгофа, после простых преобразований, получим

(1)

(здесь индекс "а" относится к параметрам дуги).

Из стационарного режима система может выйти за счет самопроизвольных, случайных возмущений параметров, например, за счет изменения напряжения источника питания на величину или скорости расхода газа на . Это приведет к отклонению тока дуги от равновесного значения на величину и изменению напряжения дуги. Для малых значений отклонений параметров можно записать

. (2)

,

где - дифференциальное сопротивление дуги. Его величина отрицательна и в дальнейшем, под величиной будем понимать его модуль.

Подставляя (2) в (1), получим уравнение для отклонений тока от стационарного значения

, (3)

где

, . (4)

Уравнение (3) и является основным уравнением рассматриваемой математической модели.

Это линейное, неоднородное дифференциальное уравнение второго порядка, известное в физике как уравнение вынужденных колебаний. Коэффициент при токе имеет смысл квадрата частоты собственных колебаний эквивалентного контура, а коэффициент при производной тока – удвоенного коэффициента затухания. Отметим, что для асимптотической устойчивости стационарного решения , они должны быть положительны [3].

Для дальнейшего анализа удобно перейти к безразмерным величинам. В качестве масштаба времени выберем и введем безразмерные время и коэффициент затухания

, .

Уравнение (3) в новых переменных будет выглядеть следующим образом

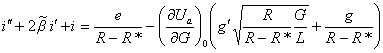(5)

Отметим, что при колебательном режиме в цепи величина лежит в пределах от нуля до единицы.

Влияние скачков напряжения источника питания на ток дуги

Рассмотрим вначале влияние скачков напряжения источника питания на ток дуги. В этом случае и уравнение (5) дает

(6)

Его решение для нулевых начальных условий может быть записано как

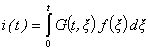(7)

где - функция Грина уравнения (6), которая, при колебательном режиме цепи, имеет вид

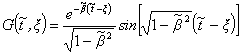(8)

т.е. представляет собой затухающую синусоиду с периодом [3].

При , положение максимума функции Грина за счет большого периода колебания изменяется незначительно и находится в точке . Поэтому и интеграл (7) также) будет иметь максимум в этой области. Его величину можно оценить как

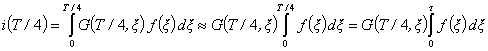(9)

где очень слабо зависит от .

Таким образом, при длительностях импульсов возмущения амплитуда возмущения тока пропорциональна интегралу от импульса возмущения напряжения источника. В свою очередь, для импульсов постоянной формы и амплитуды, этот интеграл пропорционален длительности импульса напряжения .

При больших длительностях импульса возмущения напряжения () максимум возмущения тока будет достигаться внутри временного интервала действия импульса и будет смещаться вдоль него с увеличением . Это значит, что примерно воспроизводится полная форма импульса возмущения .

Влияние коэффициента затухания на величину импульса возмущения тока будет определяться зависимостью функции Грина (8) от . В точке максимума тока ее можно оценить следующим образом

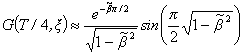(10)

Это довольно медленно убывающая функция, которая, при увеличении от 0 до 1, уменьшается от 1 до ~0,4. Для практических целей достаточно взять .

Влияние скачков скорости расхода газа на ток дуги

Основное уравнение математической модели (5) для этого случая запишется в виде

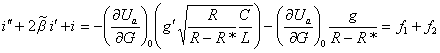(11)

В силу линейности уравнения, его решение будет являться суммой решений уравнений с правыми частями и . Свойства решения с правой частью были проанализированы в предыдущем разделе. Как было там же показано, амплитуда возмущения тока дуги при малых длительностях импульса возмущения, пропорциональна интегралу от правой части уравнения. Интеграл от равен

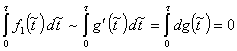
в силу конечности длительности существования возмущения скорости расхода газа g. Поэтому изменение тока дуги, вызванное действием будет значительно меньше изменения тока, вызванного действием и им, в первом приближении, можно пренебречь. Следовательно, для возмущения тока дуги, вызванного скачками скорости расхода газа, остаются в силе все выводы предыдущего анализа.

Расчет параметров цепи питания плазмотрона

Как показывает проведенный анализ, амплитуда возмущения тока дуги уменьшается пропорционально длительности импульса изменения внешнего параметра при (для определенности будем говорить о напряжении источника питания.

Этот вывод определяет условие для выбора собственной частоты системы

,

где дает величину порядка, на который надо уменьшить импульс возмущения.

Выбор собственной частоты фиксирует величину произведения . Величина индуктивности определяется из условия согласно (4). Определение величин и позволяет найти и значение .

Приведем пример использования предложенной методики. Пусть скачок напряжения источника питания в цепи с R=1 Ом и R^* =0.6 Ом имеет форму прямоугольного импульса с амплитудой 1В и длительностью . Максимальное изменение тока дуги, которое он может вызвать, равно 2,5 А. Требуется уменьшить это возмущение на порядок. Расчет по приведенной схеме дает: , , , . Форма импульса возмущения тока дуги при этих параметрах показана на рисунке 2.

Как и требовалось, его амплитуда уменьшилась на порядок по сравнению с максимально возможной. Длительность возмущения при этом значительно возросла. Если есть жесткие требования к ее величине, придется искать компромисс между уменьшением амплитуды и увеличением длительности возмущения.

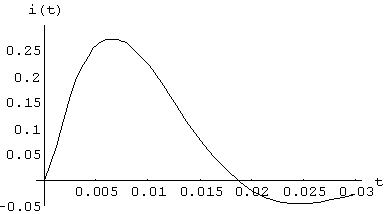
Рисунок 2 - Импульс возмущения тока дуги

ЗАКЛЮЧЕНИЕ

Рассмотрена математическая модель, описывающая динамику развития возмущений тока дуги плазмотрона, вызванных влиянием малых случайных изменений напряжения источника питания и скорости расхода продуваемого газа. На основе проведенного анализа модели предложена методика расчета параметров схемы питания плазмотрона, позволяющая уменьшить величину возмущения тока дуги.

Литература

1. Даутов Г. Ю. Плазмотроны со стабилизированными электрическими дугами / Г. Ю. Даутов, В. Л. Дзюба, И. Н. Карп – Киев: Наук. Думка, 1984. – 168 с.

2. Устойчивость горения электрической дуги. – АН СССР, Сибирское отделение, Институт теплофизики. – Новосибирск, 1973. – 151 с.

3. Зельдович Я. Б. Элементы прикладной математики / Я. Б. Зельдович, А.Д.Мышкис – М.: Наука, 1967. – 648 с.