Физика/7. Оптика

Одаренко Е. Н., Пих А. Б., Сашкова Я. В.

Харьковский национальный университет радиоэлектроники, Украина

РАССЕЯНИЕ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ НА ДИЭЛЕКТРИЧЕСКОМ ДВУХСЛОЙНОМ ЦИЛИНДРЕ

Задача о рассеянии электромагнитных волн цилиндрическими объектами является одной из основных при исследовании свойств электродинамических структур разной сложности [1]. Подобные структуры составляют основу для многих устройств антенной техники, а также используются для моделирования различных волноведущих систем. Например, оптического волокна [2]. Для моделирования волоконной структуры необходимо рассматривать задачу о рассеянии электромагнитного излучения двухслойными цилиндрами, поскольку сердцевина волокна и оболочка имеют разные материальные параметры. Следует также отметить, что цилиндрические структуры с диэлектрическими покрытиями различной толщины широко используются для создания различных функциональных устройств: управляемых фотонных кристаллов, элементов антенн, различных диагностических приборов и т.д.

Кроме того, именно двухслойный цилиндр обычно рассматривается в задачах, связанных с явлением электромагнитной маскировки (cloaking). В этом случае внешний слой изготавливается из метаматериала с отрицательным показателем преломления [3].

В данной работе рассматривается задача о рассеивании плоской электромагнитной волны, в которой моделируется лазерное излучение, на двухслойном диэлектрическом цилиндре с произвольными значениями показателей преломления в различных слоях. Эта задача является базовой для многих приложений в волоконной оптике, радиолокации, диагностике диэлектрических покрытий и т.д. На основе аналитического решения созданы средства визуализации пространственного распределения различных характеристик рассеянного электромагнитного поля, что обеспечивает наглядность представления результатов и облегчает понимание основных физических закономерностей.

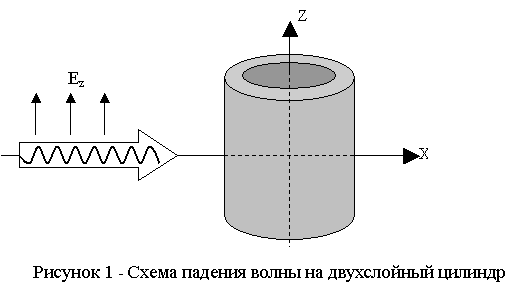
На рис. 1 представлена схема нормального падения волны на бесконечный двухслойный диэлектрический цилиндр с произвольными материальными параметрами. Образующая цилиндра – ось Oz. Показатель преломления сердцевины обозначим n₁, оболочки – n₂. Радиус сердцевины цилиндра r, радиус цилиндра с оболочкой R. Вдоль оси Ox падает электромагнитная монохроматическая волна с параллельной поляризацией (вектор напряженности электрического поля параллелен образующей цилиндра).

Выражения для напряженности электрического поля в цилиндрических координатах представляются в виде:

· Падающая волна 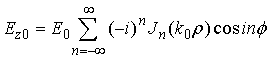(1)

· Рассеянная волна 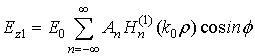(2)

· Поле внутри цилиндра 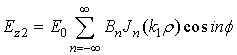(3)

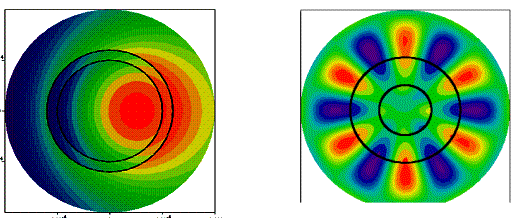
· Поле внутри слоя 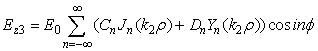(4)

Здесь: – функция Бесселя, – функция Неймана, – функция Ханкеля 1-го рода, , , – волновые числа окружающей среды, цилиндра и слоя соответственно, , , , – амплитудные коэффициенты.

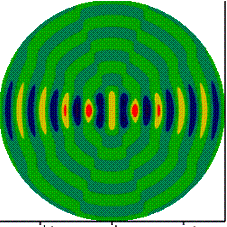
Так как выражения для полей (1) – (4) являются бесконечными рядами, то при расчетах возникает необходимость ограничиться конечным числом слагаемых. Для определения максимального индекса суммирования использовалось представление плоской волны через цилиндрические функции (1). На рис. 2 представлены результаты расчета пространственного распределения действительной части напряженности электрического поля для двух значений . Очевидно, что для выбранных параметров системы при суммировании необходимо удерживать не менее 50 слагаемых.

(а) (б)

Рисунок 2 – Пространственное распределение напряженности поля

плоской волны: (а) n = 5, (б) n = 25

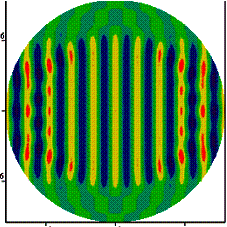
На рис. 3 представлены результаты расчета пространственного распределения напряженности электрического поля для различных значений материальных параметров и относительных размеров слоев исследуемой структуры.

(а) (б)

Рисунок 3 – Результаты расчетов

На рисунке 3(а) представлено пространственное распределение для таких параметров задачи: ; ; ; . В этом случае фактически происходит рассеяние волны на двухслойном тонком цилиндре и видна фокусировка излучения внутри структуры и в области за цилиндром.

На рисунке 3(б) параметры следующие: ; ; ; . Очевидно, что здесь реализуется распределение поля, характерное для мод шепчущей галереи. Следует отметить, что данное распределение отличается высокой чувствительностью к изменению толщины слоев структуры. Следовательно, решение задачи можно использовать при разработке систем контроля геометрических размеров многослойных диэлектрических структур.

Список источников

1. Balanis C.A. Advanced engineering electromagnetic. John Wiley & Sons. – 1989. – 981 pp.

2. Owen J.F., Barber P.W., Messinger B.J., Chang R.K. Determination of optical-fiber diameter from resonances in the elastic scattering spectrum // Optics letters. – 1981. – Vol.6, No.6. – Р. 272-274.

3. Zolla F., Guenneau S., Nicolet A., Pendry J. Electromagnetic analysis of cylindrical invisibility cloaks and the mirage effect // Optics letters. – 2007. – Vol. 32, No. 9. – P. 1069-1071.