Строительство и архитектура / 7. Водоснабжение и канализация
К.т.н. Калякин А.М., Чеснокова Е.В., Сауткина Т.Н.
Саратовский государственный технический университет
имени Гагарина Ю.А., Россия
Особенности кинематики течения перед
цилиндром при обтекании его открытым потоком.
Особенности решения задачи при
заданных вспомогательных функциях.
Как и
в предыдущих частях необходимо выбрать для основных составляющих скорости – ![]() ,
, ![]() и
и ![]() функции – сомножители
с целью удовлетворения граничных условий.
функции – сомножители
с целью удовлетворения граничных условий.
Составляющую
![]() в общем случае выбираем в виде:
в общем случае выбираем в виде:
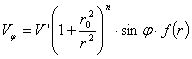 , (1)
, (1)
Условие
![]() при
при ![]() выполнено,
как и в предыдущем случае выбором
выполнено,
как и в предыдущем случае выбором ![]() .
.
Возможно
задать функцию ![]() в виде
в виде
![]() , (2)
, (2)
И
такую, чтобы:
![]() при
при ![]() , (3)
, (3)
и
![]() при
при ![]() . (4)
. (4)
Возможно
выбрать ![]() в таком виде [1]:
в таком виде [1]:
![]() (5)
(5)
или
![]() . (6)
. (6)
окончательно имеем:
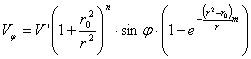 . (7)
. (7)
Выражение
для ![]() получим из уравнения неразрывности:
получим из уравнения неразрывности:
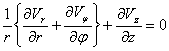 (8)
(8)
или
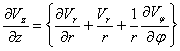 . (9)
. (9)
Интегрируя
(9) в пределах от ![]() до
до ![]() , получим:
, получим:
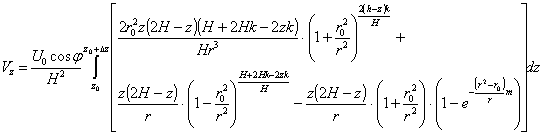 (10)
(10)
Из (10)
видно, что:
1.
При всех остальных фиксированных
параметрах ![]() принимает наибольшее значение при
принимает наибольшее значение при ![]() (на осевой плоскости);
(на осевой плоскости);
2. ![]() при
при ![]()
3. ![]() при
при ![]()
4.
![]() при
при ![]() .
.
Выражение
для давления также возможно выбрать в нескольких формах, в частности,
![]() , (11)
, (11)
где ![]() – некоторый неизвестный пока коэффициент
– некоторый неизвестный пока коэффициент
Можно
также использовать следующий прием для определения давления.
Для
определения давления в некоторой точке с координатами ![]() применим уравнение Бернулли в виде:
применим уравнение Бернулли в виде:
![]() (12)
(12)
Величины
![]() и
и ![]() считаются известными (для
считаются известными (для ![]() существуют формулы, рассматривавшиеся выше).
существуют формулы, рассматривавшиеся выше).
Для ![]() возможно предположить разные выражения; одно из простейших имеет
вид:
возможно предположить разные выражения; одно из простейших имеет
вид:
![]() , (13)
, (13)
где ![]() – неизвестный пока безразмерный
коэффициент.
– неизвестный пока безразмерный
коэффициент.
Из (12)
давление ![]() выразится как:
выразится как:
![]() (14)
(14)
Выражение
(14) логично применять, когда последовательно выбираются точки на одной линии
тока.
В (14)
как обычно ![]() ,
, ![]()
Для
решения имеем систему трёх дифференциальных уравнений движения несжимаемой
жидкости и три неизвестных коэффициента.
Решение
этой системы предлагается получить в отдельных точках; для удобства всю область
течения вокруг обтекаемого тела (цилиндра) разбивают условно на
пространственные ячейки, например, в виде кубов, и вычисляют компоненты скорости
и давление в центрах этих ячеек.
При
этом, полагая внутри каждой ячейки неизвестные коэффициенты постоянными в ее
пределах, допускается возможная неточность состоящая в том, что на границах
соседних ячеек возможны скачки как в значениях коэффициентов, так и в значениях компонентов скорости. Решения
ищутся последовательно в соседних ячейках, продвигаясь из набегающего потока.
Это обусловлено тем, что приходится решать нелинейные уравнения, имеющие
несколько наборов корней, и, таким образом, удастся выбрать в данной точке
набор, близкий к предыдущему и обойти неоднозначность решения (то есть выбрать
нужный набор).
Возможно
предложить и другой прием расчёта, отличающийся от способа разбиения
пространства обтекания на ячейки.
Так же
как и раньше, расчёт начинается из точек набегающего потока. В каждой
предыдущей точке находится вектор скорости (его направление) и в этом
направлении на определенном расстоянии выбирается следующая точка для расчета
компонентов скорости и давления.
Таким
образом, грубо говоря, расчет проводится вдоль линии тока.
Выше
были предложены выражения для компонентов скоростей; в уравнения подставляются
как эти выражения, так и производные от них. Поэтому целесообразно, видимо,
вычислять аналитически (то есть точно) эти производные, а не определять их
приближенно численными методами.
Алгоритм
решения с целью нахождения неизвестных
коэффициентов (а, следовательно, и численных значений компонентов скорости) в
точке можно предложить следующий:
1.
Задаются все функциями (с
неизвестными постоянными);
2.
Координаты заданной точки
подставляются в эти функции и их производные;
3.
Решается алгебраическая система трех
уравнений движения (нелинейных) относительно неизвестных коэффициентов;
4.
В данной точке определяются
компоненты скоростей и давления.
Литература:
1.
Калякин
А.М. Метод решения уравнений Навье-Стокса для обтекания препятствий типа
мостовой опоры (с использованием эвристических гипотез). Совершенствование
методов гидравлических расчетов водопропускных и очистных сооружений: межвуз.
науч. сб. Саратов: Сарат. гос. Техн. ун-т, 1996. С. 68-74.