Кононенко А. Д., Жученко О. А.

Національний технічний університет України «КПІ», Україна

Оптимальне керування випарником у

процесі виробництва поліізобутилену

Процес полімеризації ізобутилену є складним технологічним об’єктом керування, оскільки високомолекулярні полімери ізобутилену можна одержати лише при дуже низьких температурах, тому ми будемо розглядати лише його частину, яка протікає у випарнику. Завдяки високій хімічній стійкості з поліізобутилену виготовляють матеріали для хімічної апаратури, труб, захисний одяг для роботи з кислотами і лугами. Поліізобутилен застосовується також у виробництві клеїв для склеювання скла, тканин, паперу та як зв’язуючий матеріал для прокладок і пористих матеріалів. Широкого застосування набуває поліізобутилен у гумовій промисловості для виробництва бутилкаучуків, які дає співполімеризація ізобутилену з невеликою кількістю ізопрену [1].

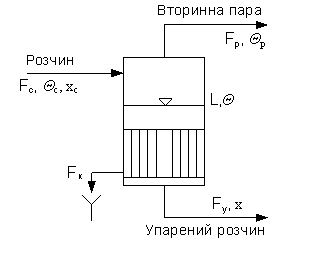
Регулятор витрати в 1-1 змінює температуру етилену у випарнику. Цей вплив є визначальним у роботі випарника. Звичайно контролю і регулюванню у випарнику підлягають:

· Температура на виході з апарату;

· Рівень у апараті;

· Витрата на виході з апарату.

Зроблені наступні припущення, що майже не впливають на фактичні умови протікання процесу, але значно спрощують розрахунок:

1) Об’єкт розглядався, як об’єкт з зосередженими параметрами.

2) Одна зосереджена акумулююча ємність.

3) Стінки апарату теплоізольовані.

Математична модель процесу випарювання представлена у вигляді рівнянь статики процесу:

1) Матеріальний баланс

2) Зміна маси речовини

3) Тепловий баланс

(

Будемо вважати за основне рівняння саме тепловий баланс і розглядати модель як рівняння теплового балансу в подальшому.

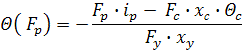
Для вирішення даної задачі оберемо квадратичний критерій, бо дана модель лінійна. Нам необхідно підтримувати на певному рівні температуру в випарнику. Тобто в критерій оптимальності включаємо температуру в випарнику:

В даному апараті ми не можемо змінювати витрату у будь-якому діапазоні, тому в цьому апараті ця витрата має лежати від 13,75 до 14,25 кг/с. Маючи статичну модель, критерій оптимальності і обмеження перетворимо задачу умовної оптимізації в безумовну:

+

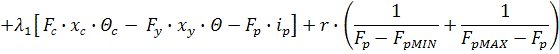
Необхідними умовами оптимальності будуть:

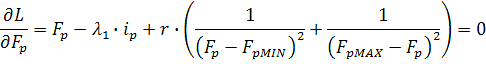
За допомогою методу штрафних функцій була розв’язана ця задача і отримані результати:

Список літератури:

1. Юкельсон И. И. Технология основного органического синтеза [Текст]. – М.: “Химия”, 1968 г. Библиогр.: с. 848. – 16000 экз.

2. Лукінюк М. В. Контроль і керування хіміко-технологічними процесами [Текст]: у 2 кн. Кн. 1: Методи та технічні засоби автоматичного контролю хіміко-технологічних процесів : навч. посіб. для студ. вищ. навч. закл., які навчаються за напрямом: «Хімічна технологія та інженерія» / М. В. Лукінюк. – К.: НТУУ «КПІ», 2012. – 336 с. : іл. – Бібліогр.: с. 328–330. –200 пр. – ISBN 978-966-622-287-2