Дополнительные признаки резонанса, общие
для линейных и нелинейных систем
Одна из
основных проблем, которая возникает при исследовании динамического поведения
нелинейных систем, состоит в достоверном определении их резонансных частот.
Представления о резонансных явлениях в нелинейных системах основаны в основном
на математических выкладках, и декларируемые теоретически резонансные
частоты на практике не всегда
соответствуют вычислительным и натурным экспериментам [1]. Поэтому для
достоверного определения резонансных частот нелинейных систем необходимо найти
такие дополнительные признаки резонансных явлений, которые бы проявлялись одинаково,
как в линейных, так и в нелинейных системах.
Общеизвестно,
что для составления уравнений движения системы наиболее часто используют
уравнение Лагранжа, которое можно записать таким образом [2,3,4]:
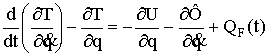 , (1)
, (1)
где 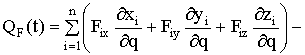 обобщённая сила,
соответствующая возмущающим силовым факторам
обобщённая сила,
соответствующая возмущающим силовым факторам ![]() ;
; ![]() кинетическая энергия системы;
кинетическая энергия системы; ![]() потенциальная энергия системы;
потенциальная энергия системы; ![]() диссипативная функция Рэлея (функция рассеивания);
диссипативная функция Рэлея (функция рассеивания); ![]() обобщённые координаты и скорости системы;
обобщённые координаты и скорости системы; ![]() коэффициент диссипации системы.
коэффициент диссипации системы.
Уравнение
(1) будет нелинейным, так как функции ![]() и
и ![]() являются нелинейными
функциями обобщённых координат. Чтобы облегчить решение практических задач,
функции
являются нелинейными
функциями обобщённых координат. Чтобы облегчить решение практических задач,
функции ![]() и
и ![]() линеаризуют, раскладывая
их в ряд Тейлора и определяя функции
линеаризуют, раскладывая
их в ряд Тейлора и определяя функции ![]() и
и![]() с точностью до
с точностью до ![]() , учитывая при этом, что
, учитывая при этом, что ![]() . Тогда выражения для кинетической и потенциальной энергий
существенно упрощаются и принимают такой вид [2,3,4]:
. Тогда выражения для кинетической и потенциальной энергий
существенно упрощаются и принимают такой вид [2,3,4]:
![]() и
и ![]() , (2)
, (2)
где ![]() называется
коэффициентом инерции, а
называется
коэффициентом инерции, а ![]() обобщённым коэффициентом жёсткости.
обобщённым коэффициентом жёсткости.
Следует
заметить, что такая аппроксимация выражений для кинетической и потенциальной
энергий системы даёт достоверные результаты расчётов, когда изменения обобщённой
координаты достаточно малы. При приближении к резонансному режиму изменения
обобщённой координаты могут быть достаточно большими, и тогда выражения (2) могут
не соответствовать действительности.
Большой
класс задач нелинейной механики составляют такие, в которых учитывается
нелинейная зависимость потенциальной функции от обобщённой координаты ![]() . Поэтому можно поставить более конкретную задачу об определении
общих признаков резонанса, как для линейных систем, когда кинетическая и
потенциальная энергии определяются выражениями (2), так и для нелинейных
систем, когда кинетическая и потенциальная энергии определяются соответственно
выражениями [1]:
. Поэтому можно поставить более конкретную задачу об определении
общих признаков резонанса, как для линейных систем, когда кинетическая и
потенциальная энергии определяются выражениями (2), так и для нелинейных
систем, когда кинетическая и потенциальная энергии определяются соответственно
выражениями [1]:
![]() и
и ![]() . (3)
. (3)
Дифференциальное
уравнение нелинейной системы с одной степенью свободы, которое описывает её
динамическое поведение на основе приведённых выше выражений (3) для
кинетической и потенциальной энергий, называется уравнением Дуффинга. Это одно
из самых простых уравнений нелинейной механики, на котором обычно апробируются
различные аналитические методы теории нелинейных колебаний.
Перед
тем как определять дополнительные признаки резонанса, уточним некоторые важные
моменты динамического поведения линейной системы с одной степенью свободы, в
которой силы трения не учитываются, т. е. когда ![]() . Рассмотрим самую простую расчётную схему динамической системы
[3], представляющую собой неподвижную опору, к которой прикреплена невесомая
пружина с жёсткостью
. Рассмотрим самую простую расчётную схему динамической системы
[3], представляющую собой неподвижную опору, к которой прикреплена невесомая
пружина с жёсткостью ![]() , и к которой, в свою очередь, прикреплено абсолютно твёрдое
тело массой
, и к которой, в свою очередь, прикреплено абсолютно твёрдое
тело массой ![]()
![]() . В качестве обобщённой координаты такой системы примем
перемещение массы от положения равновесия вдоль продольной оси х, т. е.
. В качестве обобщённой координаты такой системы примем
перемещение массы от положения равновесия вдоль продольной оси х, т. е. ![]() . Если на систему действует гармоническая сила
. Если на систему действует гармоническая сила ![]() , где
, где ![]() соответственно максимальная амплитуда внешней силы, частота
её изменения и начальная фаза, которая определяет значение внешней силы в
начальный момент времени, т. е.
соответственно максимальная амплитуда внешней силы, частота
её изменения и начальная фаза, которая определяет значение внешней силы в
начальный момент времени, т. е. ![]() , то её движение
описывается таким уравнением [2,3,4]
, то её движение
описывается таким уравнением [2,3,4]
![]() , (4)
, (4)
или в векторной форме
![]() , (5)
, (5)
где ![]() силы инерции;
силы инерции; ![]() силы упругости;
силы упругости; ![]() внешняя гармоническая
сила.
внешняя гармоническая
сила.
В теории
линейных колебаний под резонансом линейной системы с одной степенью свободы
понимают совпадение частоты возмущающей силы ![]() с собственной частотой
системы
с собственной частотой
системы 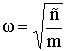 и сопровождающие его
явления [2]. Сопровождающие совпадение частот явления связаны, прежде всего, с
существенным возрастанием амплитуды колебаний системы и определёнными фазовыми
сдвигами между её силовыми компонентами [2,3,4]. Поэтому колебательные процессы
линейных систем рассматриваются в научно-технической литературе с точки зрения
изменения величины амплитуды и фазы колебаний от частоты внешней силы, т. е.
исследованию подвергаются амплитудно-частотные и фазочастотные характеристики.
В гораздо меньшей степени в колебательных процессах изучены законы
взаимодействия действующих в исследуемой системе сил. В работе [5] такие
исследования есть, но они не доведены до логического конца, и поэтому некоторые
особенности резонансных колебаний остались не выясненными. В этой работе
утверждается, что сила упругости
и сопровождающие его
явления [2]. Сопровождающие совпадение частот явления связаны, прежде всего, с
существенным возрастанием амплитуды колебаний системы и определёнными фазовыми
сдвигами между её силовыми компонентами [2,3,4]. Поэтому колебательные процессы
линейных систем рассматриваются в научно-технической литературе с точки зрения
изменения величины амплитуды и фазы колебаний от частоты внешней силы, т. е.
исследованию подвергаются амплитудно-частотные и фазочастотные характеристики.
В гораздо меньшей степени в колебательных процессах изучены законы
взаимодействия действующих в исследуемой системе сил. В работе [5] такие
исследования есть, но они не доведены до логического конца, и поэтому некоторые
особенности резонансных колебаний остались не выясненными. В этой работе
утверждается, что сила упругости ![]() до резонанса по фазе
совпадает с перемещением системы
до резонанса по фазе
совпадает с перемещением системы ![]() и с внешней
гармонической силой
и с внешней
гармонической силой ![]() и находятся в противофазе
с силой инерции
и находятся в противофазе
с силой инерции ![]() , т. е. разность векторов силы упругости и инерции равна
вектору внешней силы, который по фазе совпадает с силой упругости.
Некорректность представленной схемы взаимодействия сил системы состоит в том,
что векторная сумма всех сил не будет равна нулю, т. е. система будет
неуравновешенной, что не согласуется с принципом Даламбера.
, т. е. разность векторов силы упругости и инерции равна
вектору внешней силы, который по фазе совпадает с силой упругости.
Некорректность представленной схемы взаимодействия сил системы состоит в том,
что векторная сумма всех сил не будет равна нулю, т. е. система будет
неуравновешенной, что не согласуется с принципом Даламбера.
Если
рассмотреть механизм возбуждения колебаний в дорезонансном режиме на основе
анализа сил, которые действуют в системе, используя уравнение (5), то его можно
представить следующим образом: внешняя гармоническая сила осуществляет упругие
перемещения системы, т. е. внешняя сила и упругие перемещения системы полностью
совпадают по фазе. Однако силы упругости, пропорциональные упругим
перемещениям, оказывают сопротивление внешней силе, и, следовательно, должны
находиться в противофазе к ней. Алгебраическая сумма внешней силы и силы
упругости системы, согласно принципу Даламбера, должна уравновешиваться силой
инерции, которая находится в противофазе с упругой силой и, следовательно,
совпадает по фазе с внешней силой. Таким образом, сумма силы инерции системы и
внешней силы уравновешивают силу упругости, поэтому уравнение равновесия сил
нужно записать в таком виде: ![]() . (6)
. (6)
Так как
вектора сил вращаются с одинаковой угловой скоростью, то можно построить
векторную диаграмму для любого момента времени, когда проекция любого вектора
на выбранную действительную ось будет определять величину силы для данного
момента времени. Такая диаграмма, согласно описанному выше характеру действия
сил в системе, показана на рис. 1 для моментов времени ![]() , где
, где ![]() период колебаний,
период колебаний, ![]() .
.
Здесь
следует заметить, что при принятой расчётной схеме системы физический механизм
возбуждения колебаний в ней одинаков и при квазистатических нагрузках, и при
сугубо динамических или околорезонансных, чего в принципе быть не может, т. е.
математическая модель описания динамического поведения системы не учитывает
проявление динамического эффекта от внешней силы.
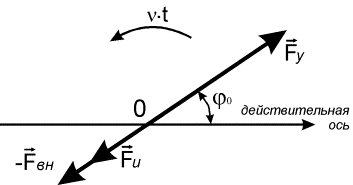
Рис. 1. Распределение сил в линейной системе с одной
степенью свободы при отсутствии сил сопротивления при нерезонансном режиме
колебаний
Динамический
эффект от внешней силы проявляется в действии внешней силы в одной фазе со
скоростью системы. Следовательно, выбранная выше математическая модель описания
динамического поведения системы с одной степенью свободы пригодна более всего
для описания дорезонансных квазистатических режимов силового воздействия, когда
скорость движения системы мала и её можно не учитывать.
Неучёт
скоростных характеристик системы приводит к тому, что принятая силовая модель в
принципе не может отобразить реальное динамическое поведение системы при
резонансном режиме, когда фазовые сдвиги между внешней силой и силой упругости
и инерции равны ![]() . Анализ диаграммы сил, представленной на рис. 2, показывает,
что система не может быть уравновешенной, т. е. силовое равенство в принципе не
может быть осуществлено. Это согласуется с традиционными выводами, которые
обычно приводятся в научно-технической литературе [2,3,4].
. Анализ диаграммы сил, представленной на рис. 2, показывает,
что система не может быть уравновешенной, т. е. силовое равенство в принципе не
может быть осуществлено. Это согласуется с традиционными выводами, которые
обычно приводятся в научно-технической литературе [2,3,4].
Для адекватного описания колебательных
процессов в системе в околорезонансных и резонансных режимах необходимо
учитывать четвёртую силу – силу сопротивления, которая обычно принимается
пропорциональной скорости перемещения системы, т. е. учёт величины и
направления вектора скорости системы осуществляется силой сопротивления, когда ![]() .
.
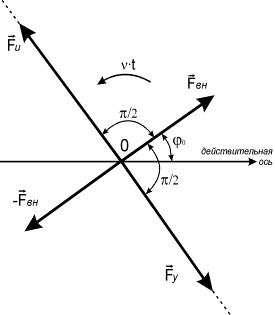
Рис. 2. Распределение сил в линейной системе с одной
степенью свободы при отсутствии сил сопротивления, при резонансном режиме
колебаний
При
дорезонансных режимах колебаний векторная диаграмма с учётом замечаний,
сделанных ранее, будет такой, как показана на рис. 3, где механизм возбуждения
колебаний системы удобнее определяется уравнением ![]() , (7)
, (7)
а силовое равенство – уравнением
![]() . (8)
. (8)
Здесь
уже тройка векторов сил (упругости, инерции и сопротивления) будет уравновешивать
внешнюю силу.
Для более удобного анализа механизма возбуждения колебаний в системе
уравнение (7) можно представить в виде системы двух уравнений (см. рис.3):
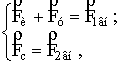 (9)
(9)
где ![]() ;
; ![]() ;
; ![]() сдвиг фаз между
внешней силой и силой упругости;
сдвиг фаз между
внешней силой и силой упругости; ![]() сдвиг фазы силы
упругости в начальный момент времени при конкретном значении частоты
сдвиг фазы силы
упругости в начальный момент времени при конкретном значении частоты ![]() внешней силы.
внешней силы.
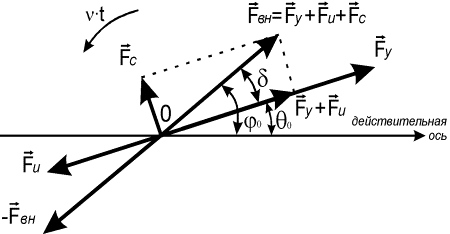
Рис. 3. Распределение сил в линейной системе с одной
степенью свободы при учёте сил сопротивления, при нерезонансном режиме
колебаний
Первое
уравнение системы (9) аналогично уравнению (5), которое позволяет установить, какая
часть амплитуды колебаний зависит от нагрузки ![]() , определяющей упругие перемещения системы. Второе уравнение
системы (9) характеризует динамический эффект от внешней силы, так как сила
, определяющей упругие перемещения системы. Второе уравнение
системы (9) характеризует динамический эффект от внешней силы, так как сила ![]() будет действовать в
фазе со скоростью системы, осуществляя, таким образом, дополнительный прирост к
амплитуде колебаний от нагрузки
будет действовать в
фазе со скоростью системы, осуществляя, таким образом, дополнительный прирост к
амплитуде колебаний от нагрузки ![]() .
.
Заметим,
что угол ![]() для каждой
определённой частоты внешней силы будет постоянным, но при изменении частоты
внешней силы от нуля до резонансной
для каждой
определённой частоты внешней силы будет постоянным, но при изменении частоты
внешней силы от нуля до резонансной ![]() угол
угол ![]() изменяется от нуля до
изменяется от нуля до
![]() , т. е. угол
, т. е. угол ![]() является функцией
частоты внешней силы. Следовательно, в квазистатическом диапазоне частот
внешней силы, когда
является функцией
частоты внешней силы. Следовательно, в квазистатическом диапазоне частот
внешней силы, когда ![]() <<
<<![]() , приоритет будет иметь составляющая внешней силы
, приоритет будет иметь составляющая внешней силы ![]() , т. е. энергия внешней силы будет затрачиваться в основном
на возбуждение упругих перемещений системы. При увеличении частоты внешнего
воздействия обе составляющие, и квазистатическая
, т. е. энергия внешней силы будет затрачиваться в основном
на возбуждение упругих перемещений системы. При увеличении частоты внешнего
воздействия обе составляющие, и квазистатическая ![]() , и динамическая
, и динамическая ![]() , будут влиять на величину амплитуды колебаний системы, а
энергия внешней силы будет затрачиваться не только на преодоление упругих сил
системы, но и на преодоление силы сопротивления. При частоте внешней силы,
соответствующей околорезонансному режиму, часть амплитуды колебаний от силы
, будут влиять на величину амплитуды колебаний системы, а
энергия внешней силы будет затрачиваться не только на преодоление упругих сил
системы, но и на преодоление силы сопротивления. При частоте внешней силы,
соответствующей околорезонансному режиму, часть амплитуды колебаний от силы ![]() будет незначительна,
поэтому основная величина амплитуды колебаний будет определяться динамической
составляющей нагрузки, т. е. силой
будет незначительна,
поэтому основная величина амплитуды колебаний будет определяться динамической
составляющей нагрузки, т. е. силой ![]() .
.
При
резонансном режиме колебаний будут иметь место строгие равенства: ![]() и
и ![]() , т. е. система уравнений (1.9) будет выглядеть таким образом:
, т. е. система уравнений (1.9) будет выглядеть таким образом:
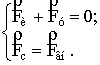 (10)
(10)
Система
уравнений (1.10) формально состоит из двух независимых уравнений и соответствует
диаграмме сил при резонансе, представленной на рис. 4.
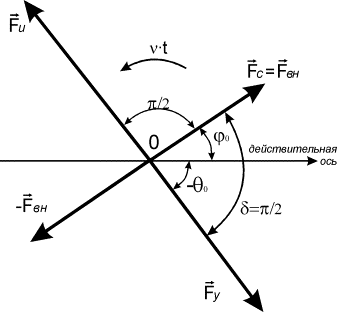
Рис. 4. Распределение сил в линейной системе с одной
степенью свободы при учёте сил сопротивления, при резонансном режиме колебаний
Внешняя сила будет полностью совпадать по
фазе с вектором скорости движения системы, вызывая близкие к максимальному
значению отклонения системы от точки равновесия, а энергия внешней силы будет
направлена исключительно на преодоление только силы сопротивления. Этот режим
колебаний соответствует известному условию резонанса, когда ![]() .
.
Первое
уравнение системы (10) говорит о том, что система колеблется как свободная консервативная
система (без трения) с амплитудой колебаний, равной её резонансной амплитуде.
Полная энергия такой системы является постоянной величиной [2,3,4], т. е. ![]() .
.
Второе
уравнение системы (10) свидетельствует о том, что энергия внешней силы
полностью поглощается силой сопротивления, так как силы действуют в противофазе
и имеют одинаковые максимальные амплитуды. В то же время направление вектора
скорости движения системы и направление вектора внешней силы полностью
совпадают, т. е. система максимально «раскачивается» внешней силой. Если
учесть, что перемещение системы описывается выражением ![]() , то амплитуда силы сопротивления
, то амплитуда силы сопротивления ![]() будет иметь выражение
будет иметь выражение
![]() [2,3,4]. Тогда,
согласно сказанному выше, при резонансе должно иметь место равенство амплитуд
силы сопротивления и внешней силы
[2,3,4]. Тогда,
согласно сказанному выше, при резонансе должно иметь место равенство амплитуд
силы сопротивления и внешней силы ![]() , т. е.
, т. е. ![]() , откуда
, откуда ![]() . Учитывая, что
. Учитывая, что ![]() [2,3,4], где
[2,3,4], где ![]() коэффициент затухания
свободных колебаний системы, приходим к такому выражению для резонансной
амплитуды
коэффициент затухания
свободных колебаний системы, приходим к такому выражению для резонансной
амплитуды ![]() , которое совпадает с тем, что обычно приводится в
научно-технической литературе [2,3,4].
, которое совпадает с тем, что обычно приводится в
научно-технической литературе [2,3,4].
Заметим,
что выявленное свойство системы не опирается явно на такое базовое понятие
теории линейных колебаний, как собственная частота ![]() .
.
Ниже, на
рис. 5, представлены графики, показывающие изменение сил системы во времени при
резонансе при ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Анализ графиков подтверждает сделанные ранее выводы о том,
что внутренние и внешняя сила системы попарно уравновешены в любой момент
времени. Вычисления проводились при значениях коэффициентов уравнения, которые
использовались в работе [3].
. Анализ графиков подтверждает сделанные ранее выводы о том,
что внутренние и внешняя сила системы попарно уравновешены в любой момент
времени. Вычисления проводились при значениях коэффициентов уравнения, которые
использовались в работе [3].
Н
|
|
Н
|
|
Рис.
1.5. Изменение сил линейной системы во времени при резонансе. ![]() силы упругости;
силы упругости; ![]() силы инерции;
силы инерции; ![]() силы сопротивления;
силы сопротивления; ![]() внешняя сила.
внешняя сила.
Верхний рисунок соответствует уравнению (8),
а нижний – уравнению (7). На нижнем графике особенно заметно проявление
динамического эффекта, когда изменение внешней силы полностью соответствует
изменению силы сопротивления. Такую форму записи уравнений целесообразно применять
тогда, когда их решение определяется численными методами, тогда по разности фаз
можно судить о близости колебательного режима к резонансному. При резонансном
режиме изменение скорости системы, а, следовательно, при форме записи уравнения
(7) и силы сопротивления полностью совпадает с изменением действия внешней
силы.
Описанные
выше процессы можно доказать с энергетической точки зрения.
Применяя
к уравнению Лагранжа (1) общеизвестные преобразования Эйлера [2, 4], можно
получить следующее равенство:
![]() , (11)
, (11)
из которого следует, что изменение полной энергии
возмущённой системы зависит от соотношения между силой сопротивления,
определяемой функцией рассеяния Ф и обобщённой силой ![]() .
.
Подставляя
выражение для перемещений ![]() в выражения для
кинетической и потенциальной энергий и складывая их, получим
в выражения для
кинетической и потенциальной энергий и складывая их, получим
![]() . (12)
. (12)
Таким
образом, полная энергия системы состоит из постоянной составляющей и переменной,
изменяющейся с двойной частотой ![]() . В этом случае экстремум функции
. В этом случае экстремум функции ![]() может быть определён
из известного условия
может быть определён
из известного условия ![]() . Тогда, согласно (12)
. Тогда, согласно (12) ![]() . (13)
. (13)
Равенство
(13) может быть выполнено при любом ![]() только при условии
равенства собственной частоты
только при условии
равенства собственной частоты ![]() системы частоте
системы частоте ![]() внешнего возмущения,
т. е. при
внешнего возмущения,
т. е. при ![]() , которое и является общеизвестным условием возникновения резонансного
режима для линейной системы с одной степенью свободы. Тогда, учитывая (12),
полная энергия системы будет иметь постоянное значение, т. е.
, которое и является общеизвестным условием возникновения резонансного
режима для линейной системы с одной степенью свободы. Тогда, учитывая (12),
полная энергия системы будет иметь постоянное значение, т. е. ![]() . (14)
. (14)
Это
означает, что при резонансном режиме изменения полной энергии в системе не
происходит. Таким образом, с энергетической точки зрения условием проявления
резонанса в линейной системе с одной степенью свободы является равенство ![]() или аналогичное ему
или аналогичное ему ![]() , причём оно полностью соответствует общепринятому условию
, причём оно полностью соответствует общепринятому условию ![]() , определяющего наличие резонанса в такой системе.
Постоянство полной энергии при резонансе рассматриваемой системы говорит о том,
что её движение описывается уравнением свободных колебаний
, определяющего наличие резонанса в такой системе.
Постоянство полной энергии при резонансе рассматриваемой системы говорит о том,
что её движение описывается уравнением свободных колебаний ![]() или в форме сил
или в форме сил ![]() .
.
В то же
время условие ![]() автоматически приводит
к равенству
автоматически приводит
к равенству ![]() . Последнее означает, что изменение энергии в системе в
результате её рассеивания полностью компенсируется изменением энергии внешнего
источника, или иными словами, рассеивание энергии в системе полностью
компенсируется поступлением в систему энергии от внешнего источника.
. Последнее означает, что изменение энергии в системе в
результате её рассеивания полностью компенсируется изменением энергии внешнего
источника, или иными словами, рассеивание энергии в системе полностью
компенсируется поступлением в систему энергии от внешнего источника.
При
резонансе силы сопротивления для системы с одной степенью свободы при
гармоническом воздействии можно выразить таким образом:
![]() ,
(15)
,
(15)
т. е. силы сопротивления действуют в противофазе с
внешней силой, так как ![]() . Отсюда следует, что при резонансе амплитуда внешней силы
должна быть равна амплитуде сил сопротивления, т. е.
. Отсюда следует, что при резонансе амплитуда внешней силы
должна быть равна амплитуде сил сопротивления, т. е. ![]() , что соответствует выводам, которые сделаны выше на основе
попарного равенства сил. Приведённые результаты свидетельствуют, что система
ведёт себя как свободная консервативная система с начальным отклонением от
положения равновесия, равным максимуму резонансной амплитуды. Этот вывод также
полностью совпадают с тем, что был сделан ранее на основе выявленного
дополнительного признака о попарном равенстве сил при резонансе системы.
, что соответствует выводам, которые сделаны выше на основе
попарного равенства сил. Приведённые результаты свидетельствуют, что система
ведёт себя как свободная консервативная система с начальным отклонением от
положения равновесия, равным максимуму резонансной амплитуды. Этот вывод также
полностью совпадают с тем, что был сделан ранее на основе выявленного
дополнительного признака о попарном равенстве сил при резонансе системы.
При
решении практических задач по определению резонансных режимов более удобно
использовать энергетический признак резонанса, если в аналитической или
численной форме удаётся получить выражение для полной энергии системы.
Ниже на рис. 6 представлены
графики изменения кинетической, потенциальной и полной энергии во времени при
резонансе, которые подтверждают сделанные выше заключения.
Дж
|
|
Рис.
6. Изменение потенциальной, кинетической и полной энергий линейной системы при
резонансе. ![]() потенциальная энергия системы;
потенциальная энергия системы; ![]() кинетическая энергия системы;
кинетическая энергия системы; ![]() полная энергия системы
полная энергия системы
Выявленные
два дополнительных признака резонанса для линейных систем с одной степенью
свободы получены на основе уравнения Лагранжа второго рода, которое справедливо
и для нелинейных систем. Поэтому следует ожидать, что попарное равенство сил и
постоянство полной энергии должно иметь место и при резонансе нелинейных
систем, потому что при других условиях, т. е. при других фазовых углах между
силовыми компонентами системы, резонансные явления возникнуть просто не могут.
Рассмотрим особенности проявления резонансных режимов в самой простой нелинейной системе с одной степенью свободы, колебательные процессы которых описываются уравнением Дуффинга [1]
![]() .
.
Согласно приведённым выше
выкладкам, уравнение Дуффинга можно записать по аналогии с системой уравнений
(9), которая в раскрытом виде будет выглядеть таким образом:
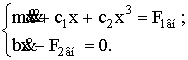 (16)
(16)
В общем
виде получить какое-либо достаточно точное аналитическое решение для системы
уравнений (16) достаточно сложно [1], что делает затруднительным анализ его
решений на всём представляющем практический интерес частотном диапазоне
изменения внешней силы. Однако при резонансном режиме, когда должно иметь место
попарное равновесие сил, такое исследование упрощается.
При
резонансе систему уравнений (16) с учётом попарного равновесия сил можно записать
таким образом:
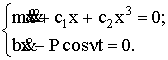 (17)
(17)
Первое уравнение после общепринятых
преобразований можно представить в таком виде: ![]() , (18)
, (18)
где ![]() собственная частота
порождающей системы, когда
собственная частота
порождающей системы, когда ![]() ;
; ![]() коэффициент,
определяющий степень нелинейности упругой характеристики.
коэффициент,
определяющий степень нелинейности упругой характеристики.
Уравнение
(18) представляет собой уравнение нелинейного осциллятора, решением которого
может быть или эллиптический косинус ![]() , или эллиптический синус
, или эллиптический синус ![]() , где
, где ![]() модуль эллиптической функции, а
модуль эллиптической функции, а ![]() резонансная частота
системы, которая отлична от собственной частоты порождающей системы. При
резонансная частота
системы, которая отлична от собственной частоты порождающей системы. При ![]() , а, следовательно, и
, а, следовательно, и ![]() , эллиптические функции вырождаются в тригонометрические, а
, эллиптические функции вырождаются в тригонометрические, а ![]() . Ниже приведены некоторые соотношения для эллиптических функций
косинуса и синуса, которыми воспользуемся для дальнейших исследований [5]:
. Ниже приведены некоторые соотношения для эллиптических функций
косинуса и синуса, которыми воспользуемся для дальнейших исследований [5]:
![]() ;
; ![]() , где
, где
![]() функция дельта
амплитуды;
функция дельта
амплитуды; ![]() ;
;
![]() ;
; ![]() . При
. При ![]()
![]() .
.
Анализ приведённых выше соотношений
показывает, что главное отличие эллиптических функций от соответствующих
тригонометрических состоит в том, что их производные представляют собой
произведение двух функций. Причём период функции дельта амплитуды ![]() отличается от периода эллиптических косинуса и синуса,
следовательно, не будет постоянного фазового рассогласования между эллиптическим синусом и косинусом и их
производными, как у тригонометрических функций. Ниже на рисунке 7 приведены графики
эллиптических функций для фазовых сдвигов между силовыми компонентами,
свойственные резонансным режимам, которые подтверждают сказанное выше.
отличается от периода эллиптических косинуса и синуса,
следовательно, не будет постоянного фазового рассогласования между эллиптическим синусом и косинусом и их
производными, как у тригонометрических функций. Ниже на рисунке 7 приведены графики
эллиптических функций для фазовых сдвигов между силовыми компонентами,
свойственные резонансным режимам, которые подтверждают сказанное выше.
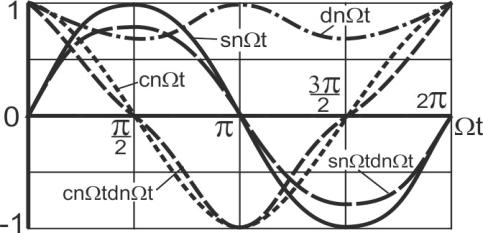
Рис. 7. Эллиптические
функции Якоби ![]() ,
, ![]() ,
, ![]() и
их производные
и
их производные
Если воспользоваться приведёнными выше
соотношениями, то, если взять в качестве решения уравнения (18) эллиптический
косинус ![]() , в виду того, что в правой части уравнения Дуффинга стоит
тригонометрический косинус, то вторую производную от
, в виду того, что в правой части уравнения Дуффинга стоит
тригонометрический косинус, то вторую производную от ![]() по
по ![]() можно представить
таким образом:
можно представить
таким образом:
![]() .
.
Выражения для силы инерции ![]() и для силы упругости
и для силы упругости ![]() идентичны и
отличаются только постоянными величинами. Чтобы соблюдалось равновесие сил, должны
выполняться равенства
идентичны и
отличаются только постоянными величинами. Чтобы соблюдалось равновесие сил, должны
выполняться равенства ![]() и
и ![]() . При этом вектор упругой силы
и вектор силы инерции, будучи равны по своей абсолютной величине, и направлены
в противоположные стороны, вращаются с одинаковой частотой
. При этом вектор упругой силы
и вектор силы инерции, будучи равны по своей абсолютной величине, и направлены
в противоположные стороны, вращаются с одинаковой частотой ![]() , но на основное их движение накладывается дополнительное,
определяемое соответствующими членами:
, но на основное их движение накладывается дополнительное,
определяемое соответствующими членами: ![]() и
и ![]() . Причём дополнительное движение векторов сил инерции и
упругости возникает на каждом полупериоде колебаний и согласовано так, чтобы
соблюдалось равновесие сил. Таким образом, вектор силы инерции и вектор силы
упругости помимо основного вращения с частотой
внешней силы
. Причём дополнительное движение векторов сил инерции и
упругости возникает на каждом полупериоде колебаний и согласовано так, чтобы
соблюдалось равновесие сил. Таким образом, вектор силы инерции и вектор силы
упругости помимо основного вращения с частотой
внешней силы ![]() периодически совершают
дополнительное колебание около некоторого среднего своего положения, отклоняясь
от него на некоторый угол
периодически совершают
дополнительное колебание около некоторого среднего своего положения, отклоняясь
от него на некоторый угол ![]() с угловой скоростью
с угловой скоростью ![]() . Под средним положением следует понимать такое положение
векторов сил упругости и инерции, при котором фазовые углы между ними и
вектором внешней силы составляют
. Под средним положением следует понимать такое положение
векторов сил упругости и инерции, при котором фазовые углы между ними и
вектором внешней силы составляют ![]() . Такое дополнительное колебание векторов сил упругости и
инерции около среднего положения можно назвать периодической фазовой
нестабильностью колебательного процесса. Очевидно, что фазовая нестабильность,
хотя и не нарушает силового равновесия всей системы, но изменяет фазовые сдвиги
между силовыми компонентами системы, которые свойственны резонансному режиму и
которые могут соблюдаться только в отдельные моменты времени, когда все векторы
сил одновременно будут проходить своё среднее положение, и фазовые углы между
ними будут равны
. Такое дополнительное колебание векторов сил упругости и
инерции около среднего положения можно назвать периодической фазовой
нестабильностью колебательного процесса. Очевидно, что фазовая нестабильность,
хотя и не нарушает силового равновесия всей системы, но изменяет фазовые сдвиги
между силовыми компонентами системы, которые свойственны резонансному режиму и
которые могут соблюдаться только в отдельные моменты времени, когда все векторы
сил одновременно будут проходить своё среднее положение, и фазовые углы между
ними будут равны ![]() . Иначе вращение векторов сил упругости и инерции не будет
равномерным, как при фазостабильном вращении, а изменение этих сил во времени будет
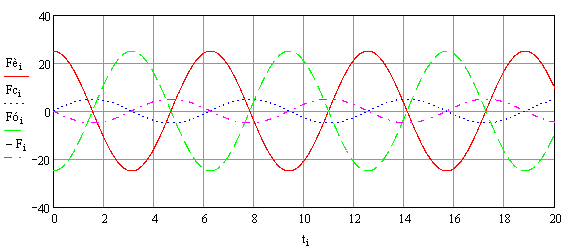
носить не гармонический, а периодический характер (рис. 8). Графики строились
при таких значениях коэффициентов уравнения Дуффинга, какие использовались в
работе [3]:
. Иначе вращение векторов сил упругости и инерции не будет
равномерным, как при фазостабильном вращении, а изменение этих сил во времени будет
носить не гармонический, а периодический характер (рис. 8). Графики строились
при таких значениях коэффициентов уравнения Дуффинга, какие использовались в
работе [3]: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
На основе приведённых соображений можно
сделать вывод, что рассогласование фаз ![]() между вектором
внешней силы и силы упругости будет зависеть не только от частоты изменения
внешней силы
между вектором
внешней силы и силы упругости будет зависеть не только от частоты изменения
внешней силы ![]() , но и от угловой скорости
, но и от угловой скорости ![]() фазовой нестабильности,
т. е. фазовый сдвиг
фазовой нестабильности,
т. е. фазовый сдвиг ![]() будет являться
функцией не только параметра
будет являться
функцией не только параметра ![]() , но и параметра
, но и параметра ![]() .
.
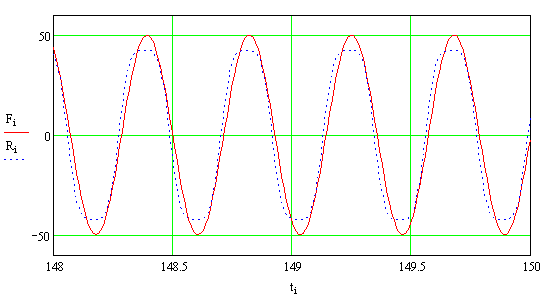
Н
|
|
Рис.
8. Изменение сил упругости ![]() и сил инерции
и сил инерции ![]() во времени при резонансном
режиме нелинейной системы
во времени при резонансном
режиме нелинейной системы
При этом заметим, что синхронное колебание
векторов сил инерции и упругости не изменяет полной энергии системы, а
оставляет её постоянной ![]() . В этом можно убедиться, если подставить выражение для перемещений
. В этом можно убедиться, если подставить выражение для перемещений
![]() и её первой производной
и её первой производной
![]() в выражения (3) для
кинетической и потенциальной энергии системы. На рис. 9 приведены графики изменения
потенциальной, кинетической и полной энергий нелинейной системы, когда её движение
описывается уравнениями (17). Вычисления проводились при значениях коэффициентов
уравнения (17), которые использовались в работе [3].
в выражения (3) для
кинетической и потенциальной энергии системы. На рис. 9 приведены графики изменения
потенциальной, кинетической и полной энергий нелинейной системы, когда её движение
описывается уравнениями (17). Вычисления проводились при значениях коэффициентов
уравнения (17), которые использовались в работе [3].
Дж
|
|
Рис.
9. Изменение потенциальной, кинетической и полной энергий нелинейной системы
при резонансе
Следует отметить отличия между графиками
энергий линейной и нелинейной систем. В линейной (фазостабильной) системе кинетическая
и потенциальная энергии равномерно распределены относительно периода колебаний
(рис 6), а в нелинейной (фазонестабильной) системе – неравномерно. Такая неравномерность
распределения энергии за период колебаний является одним из признаков
проявления периодической фазовой нестабильности системы.
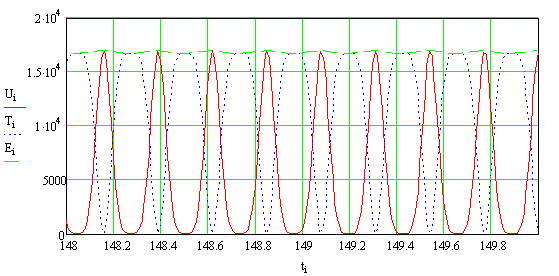
Теперь
исследуем, будет ли иметь место
равновесие между силой трения и внешней силой, т. е. будет ли выполняться
равенство ![]() или
или ![]() . Используя приведённые выше соотношения для эллиптических
косинуса и синуса, можно записать это равенство в таком виде:
. Используя приведённые выше соотношения для эллиптических
косинуса и синуса, можно записать это равенство в таком виде:
![]() . (19)
. (19)
Анализ
выражения (19) показывает, что даже при равенстве амплитуд сил, т. е. когда
амплитуда внешней силы равна амплитуде силы сопротивления ![]() , равенства между левой и правой частью в выражении (19) соблюдаться
не будет. Кроме того, согласно графикам на рисунке 7 произведение эллиптического
косинуса на функцию дельта амплитуды уменьшает амплитуду колебаний, поэтому равенство
амплитуд не будет и при
, равенства между левой и правой частью в выражении (19) соблюдаться
не будет. Кроме того, согласно графикам на рисунке 7 произведение эллиптического
косинуса на функцию дельта амплитуды уменьшает амплитуду колебаний, поэтому равенство
амплитуд не будет и при ![]() . Это равенство будет справедливо только в отдельные моменты
времени
. Это равенство будет справедливо только в отдельные моменты
времени ![]() , так как сила сопротивления обладает периодической фазовой
нестабильностью и совершает дополнительные периодические колебания около
среднего положения в пределах угла
, так как сила сопротивления обладает периодической фазовой
нестабильностью и совершает дополнительные периодические колебания около
среднего положения в пределах угла ![]() с угловой скоростью
с угловой скоростью ![]() (см. рис. 10). Поэтому, хотя общее равновесие сил
системы будет соблюдаться, но будут постоянно нарушаться фазовые сдвиги, которые
свойственны резонансному режиму, и соответствовать они резонансу могут только
тогда, когда сила сопротивления будет проходить через среднее положение.
(см. рис. 10). Поэтому, хотя общее равновесие сил
системы будет соблюдаться, но будут постоянно нарушаться фазовые сдвиги, которые
свойственны резонансному режиму, и соответствовать они резонансу могут только
тогда, когда сила сопротивления будет проходить через среднее положение.
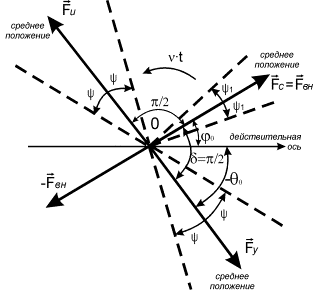
Рис. 10. Распределение сил в нелинейной системе с
одной степенью свободы при учёте сил сопротивления, при околорезонансном режиме
колебаний
Дополнительное
колебание вектора силы сопротивления около своего среднего положения также
приводит к изменению фазового угла ![]() . Таким образом, окончательно можно утверждать, что угол
. Таким образом, окончательно можно утверждать, что угол ![]() будет являться функцией
и аргумента
будет являться функцией
и аргумента ![]() (
(![]() и
и ![]() ), т. е.
), т. е. ![]() , причём последние два аргумента приводят к нарушению
равенства
, причём последние два аргумента приводят к нарушению
равенства ![]() за исключением
отдельных моментов времени, когда векторы сил упругости, инерции и
сопротивления одновременно проходят своё среднее положение.
за исключением
отдельных моментов времени, когда векторы сил упругости, инерции и
сопротивления одновременно проходят своё среднее положение.
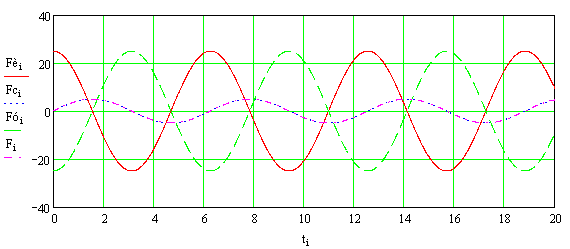
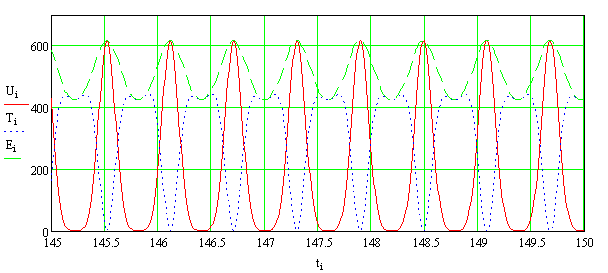
Из сказанного выше следует, что при
воздействии гармонической силы на нелинейную систему сила сопротивления будет
носить периодический, а не гармонический характер, т. е. полного совпадения
сил, как при резонансе линейной системы (рис. 5), не будет. На рисунке 11
показан характер изменения внешней гармонической силы и силы сопротивления,
который подтверждает сделанные выше заключения.
Н
|
|
Рис.
11. Изменение внешней гармонической силы ![]() и силы сопротивления
и силы сопротивления ![]() нелинейной системы во
времени
нелинейной системы во
времени
Следует обратить внимание на то, что речь
идёт об одной резонансной частоте, а не о серии резонансных частот, которые
якобы присущи нелинейным системам [1,6]. Из вышесказанного следует, что резонансный
режим нелинейной системы, который описывается уравнениями (17), в реальности возникнуть
не может.
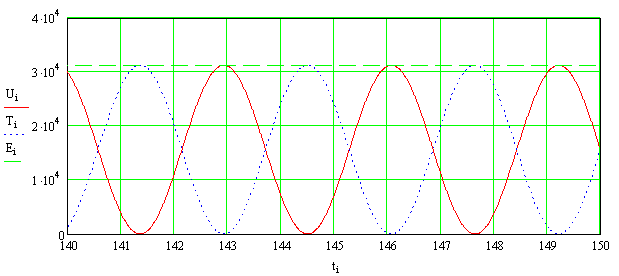
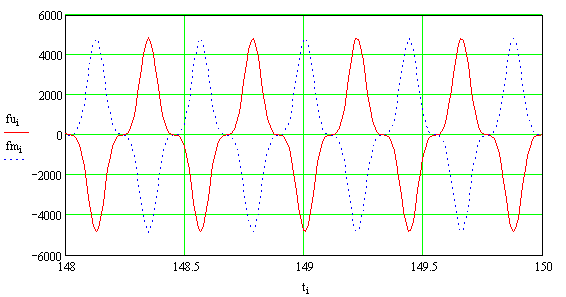
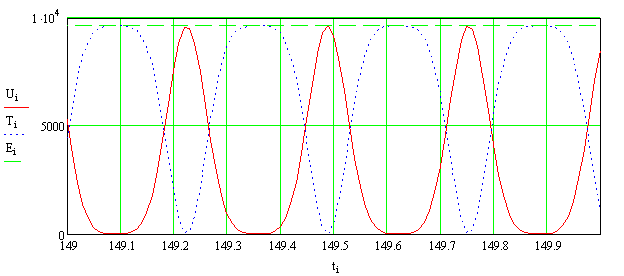
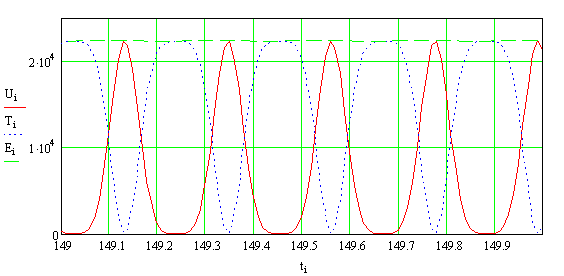
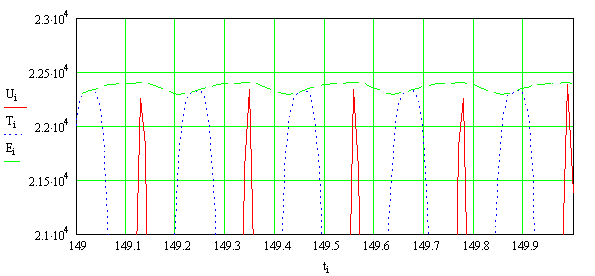
На рисунке 12 приведены графики изменения
кинетической, потенциальной и полной энергий при нулевых начальных условиях
движения системы, а на рисунках 13, 14 и 15 приведены соответствующие графики
при ненулевых начальных условиях движения системы, когда ![]() и
и ![]() .
.
Анализ
графиков позволяет сделать заключение, что в нелинейной системе, динамическое
поведение которой описывается уравнением Дуффинга, резонансных режимов, в
строгом понимании этого явления, не возникает. Однако в ней возникают режимы
близкие к резонансным (околорезонансные режимы), причём такие режимы возникают
при определённом сочетании величины начальных условий движения системы и
амплитуды (интенсивности) внешнего воздействия, когда фазовая нестабильность
нелинейной системы проявляется незначительно. Это явление установлено впервые.
Дж
|
|
Рис.
12. Изменение потенциальной, кинетической и полной энергий нелинейной системы с
одной степенью свободы при нулевых начальных условиях и при значении частоты ![]() , соответствующей максимальному значению АЧХ
, соответствующей максимальному значению АЧХ
Дж
|
|
Рис. 13. Изменение потенциальной,
кинетической и полной энергий нелинейной системы с одной степенью свободы при
ненулевых начальных условиях ![]() и при значении частоты
и при значении частоты
![]() , соответствующей максимальному значению АЧХ
, соответствующей максимальному значению АЧХ
|
|
Дж
Рис. 14. Изменение потенциальной,
кинетической и полной энергий в системе, движение которой описывается
уравнением Дуффинга, при ненулевых начальных условиях ![]() и при значении частоты
и при значении частоты
![]() , соответствующей максимальному значению АЧХ
, соответствующей максимальному значению АЧХ
Дж
|
|
Рис. 15. Изменение
потенциальной, кинетической и полной энергий в системе, движение которой
описывается уравнением Дуффинга, при ненулевых начальных условиях ![]() и при значении
частоты
и при значении
частоты ![]() , соответствующей максимальному значению АЧХ
, соответствующей максимальному значению АЧХ
При нулевых начальных условиях движения
системы и близких к ним околорезонансных режимов в нелинейных системах вообще
не возникает.
Если сравнить значение резонансной частоты
нелинейной системы, динамическое поведение которой описывается уравнением
Дуффинга, полученное одним из традиционных аналитических методов нелинейной
механики, со значением, полученным численными методами, то можно сказать, что
резонансная частота нелинейной системы является некоторой предельной её
характеристикой, к которой система может стремиться, но не может её достигнуть
из-за своей фазовой нестабильности. Можно сделать и более общий вывод:
представление резонансного режима нелинейной системы в виде одной гармоники,
соответствует тому предельному колебательному процессу, к которому стремится
нелинейная система, но в принципе не может достигнуть его из-за своей фазовой
нестабильности. Поэтому и резонансные амплитуда и частота, при аппроксимации резонансного
режима одной гармоникой, также будут являться некими предельными
характеристиками. Существенный недостаток, когда фазонестабильный процесс
аппроксимируется фазостабильным гармоническим процессом, состоит в том, что
предельный колебательный процесс не зависит от начальных условий движения
системы, в то время как фазонестабильный колебательный процесс существенно
зависит от них.
В нелинейной системе с одной степенью
свободы может возникать только один околорезонансный режим на частотах, близких
к её резонансной частоте, если фазовая нестабильность сил упругости, инерции и
сопротивления будет проявляться незначительно, т. е. углы ![]() и
и ![]() , а, следовательно, и угловые скорости
, а, следовательно, и угловые скорости ![]() и
и ![]() , будут достаточно малыми. В этом случае амплитуда вынужденных
колебаний будет близка по величине к амплитуде резонансного режима. Других
резонансных режимов субгармонических, супергармонических и комбинационных в
нелинейной системе возникнуть не может.
, будут достаточно малыми. В этом случае амплитуда вынужденных
колебаний будет близка по величине к амплитуде резонансного режима. Других
резонансных режимов субгармонических, супергармонических и комбинационных в
нелинейной системе возникнуть не может.
Литература
1. Крюков Б. И. Вынужденные колебания
существенно нелинейных систем. М.: Машиностроение, 1984. – 216 с.
2. Бабаков И. М. Теория колебаний /4-е
изд., испр. М.: Дрофа, 2004. – 591 с.
3. Стрелков С. П. Введение в теорию
колебаний. М.: Наука, 1964. – 438 с.
4. Яблонский А. А., Норейко С. С. Курс теории колебаний. М.: Лань. 2003.
– 256 с.
5. Моисеев Н. Н. Асимптотические методы нелинейной механики. М.: Изд.
«Наука», главная редакция физико-математической литературы, 1969.– 380 с.
6. Боголюбов Н. Н., Митропольский Ю. А.
Асимптотические методы в теории нелинейных колебаний. Т.3. М.: Наука, 2005. –
605 с.