УДК 621.852.13

Ундирбаев М.С. к.т.н., Нуржан Д.Ж докторант PhD.,

Ахпанов К.Ш. магистрант

Казахский национальный аграрный университет, г. Алматы, Казахстан

Кинематика зубчатого дифференциала с двумя выходными звеньями

Основным вопросом при анализе любой передачи является оценка ее кинематических и динамических показателей. К кинематическим показателям передач относятся числа оборотов, угловые и окружные скорости отдельных звеньев, передаточные числа передач.

В рассматриваемой передаче вторая степень свободы заключается в возможном независимом вращении эпициклической шестерни. Рассмотрено закономерности взаимодействия угловых скоростей и моментов звеньев дифференциала, приводящие к его силовой адаптации.

Как известно, двухподвижные механизмы или механизмы с двумя степенями свободы (например, механизм зубчатого дифференциала) служат либо для разложения одного движения на два, либо для сложения двух движений в одно [1,2,3,4].

При разложении движений, силовой поток входного звена с заданными параметрами, то есть с заданным моментом и угловым перемещением (или угловой скоростью) раскладывается на два силовых потока двух выходных звеньев. В каждом выходном силовом потоке момент зависит от перемещения (скорости), то есть имеет место силовая адаптация каждого выходного звена к внешней нагрузке за счет его перемещения. Всякая дифференциальная передача, в общем случая состоит из отдельных связанных между собой трехзвенных зубчатых механизмов. В этом механизме могут быть два входа и один выход или один вход и два выхода. В первом случае зубчатый дифференциал предназначен для сложения движения входных звеньев, во втором случае – для разделения движения входного звена.

Степень свободы относительно подвижных звеньев рассматриваемых дифференциальных механизмов определяется по формуле П.Л.Чебышева

(1)

где n – число подвижных звеньев, включая сателлиты;

р₅ и р₄ – число кинематических пар пятого и четвертого класса [2]

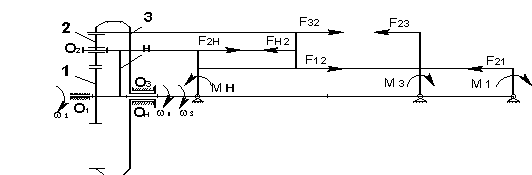
Рисунок 1 – Схема зубчатого дифференциального механизма и картина сил действующий на звено

Число подвижных звеньев в механизме , число вращательных пар V класса . Это три пары , и , которые входят звенья 1, 3 и Н со стойкой, и пара , в которую входит водило Н и звено 2. Число пар IV класса . Это входящие в зацепление колеса 1, 2 и 3, 2. Следовательно, по структурной формуле число степеней подвижности механизма

Таким образом, для определение движения механизма он должен иметь заданными законы движения двух звеньев, т.е. иметь две обобщенные координаты. Силовая адаптация зубчатого дифференциала состоит в автоматическом приведении в соответствие внешних моментов, изменяющимся моментам сопротивления за счет изменения их угловых скоростей при постоянных параметрах мощности входного звена [2].

Рассмотрим закономерности взаимодействия угловых скоростей и моментов звеньев дифференциала, приводящие к его силовой адаптации.

Кинематика зубчатого дифференциала (рисунок 1) определяется формулой, связывающей угловые скорости водила Н, ω_Н и центральных колес 1 и 3 – ω₁ и ω₃ в обращенном движении при неподвижном водиле Н

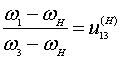, (2)

где - передаточное отношение от колеса 1 к колесу 3 при неподвижном водиле Н.

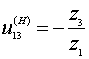
где z₁, z₃ – числа зубьев 1 и 3.

Уравнение кинематики (2) связывает три независимых параметра угловой скорости ω_Н, ω₁ и ω₃ при известном передаточном отношении . Задание двух параметров угловой скорости приводит к определению третьего параметра. Для двухподвижного зубчатого дифференциального механизма (рисунок 1) с внешними моментами М_Н, М₁, М₃ на звеньях Н, 1, 3 условие равновесия по принципу возможных перемещений с учетом фактора времени принимает вид:

. (3)

Формула (3) в общем случае не позволяет отделить моменты от угловых скоростей. При этом отдельная от моментов связь, между угловыми скоростями звеньев существует:

. (4)

Для двухподвижного механизма два уравнения (3) и (4) связывают шесть параметров мощности (М_Н, ω_Н, М₁, ω₁, М₃, ω₃). Четыре параметра, являются независимыми или задаваемыми. Это две угловые скорости и два момента, или одна угловая скорость и три момента. При этом, однозначное соответствие моментов (или угловых скоростей) отсутствует, то есть задание только моментов (или только угловых скоростей) не позволяет определить остальные параметры. Таким образом, в двухподвижном механизме определимость параметров мощности имеет место только при моментах, зависящих от угловых скоростей (заданными должны быть моменты и угловые скорости) [1,2,4].

Кроме того, из условия статического равновесия моментов имеем

(5)

откуда момент на ведомом вале

Поставляя значение в равенство (3), получим

или

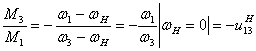
Тогда

(6)

где имеет место только при неподвижном водиле Н.

Из уравнения (6) видно, что момент на любом нагруженном звене 3 дифференциальной передачи с двумя степенями свободы определяется как произведение момента на ведущем вале на передаточное отношение от него к данному звену при остановленном вале Н со знаком минус.

The summary

In this article degree of freedom and transfer relations of the differential mechanism is considered definitions

Использованные источники

1. Артоболевский И.И. Теория механизмов и машин. М., «Гостехиздат», 1951г.

2. Пронин Б.А. Некоторые вопросы расчета и конструирования вариаторов. В сб. «Передачи в машиностроении». М., Машгиз, 1951.

3. Беступенчатая передача Жунисбекова П.Ж. с кинематической цепью управления Отчет ОНИР /КазСХИ; Руководитель П.Ж.Жунисбеков. Алматы, 1995, -N ГР0194РК01289; Инв.N0294РК00151. - 55 с.

4. Регулируемая передача Жунисбекова П. A.C.CCCP N1788365 кл. F 16 H 3/44, патент РК N 647.