Магистрант Тихонов Е. В.

Омский государственный технический университет

ЦИФРОВЫЕ СИСТЕМЫ ДИНАМИЧЕСКОЙ ТЕРМОКОМПЕНСАЦИИ КВАРЦЕВЫХ ГЕНЕРАТОРОВ

Одним из основных элементов электрической цепи современных электронных генераторов зачастую являются кварцевые резонаторы. Их использование обусловлено высокими значениями надежности, стабильности, добротности, а также легкой доступностью, простотой использования и малыми размерами. Все эти характеристики и факторы дают возможность использования кварцевых резонаторов не только в гражданских радиоэлектронных устройствах и бытовых приборах, но также делают их пригодными и для военного применения.

Открытие пьезоэффекта в 1880 г. братьями Кюри положило начало развитию резонаторов на кристаллах кварца, а также техники использующей такие резонаторы.

Кварцевый резонатор – это электромеханическое устройство, основной частью которого является пьезоэлектрический элемент, выполненный из кристалла кварца. Кристаллы кварца обладают прямым и обратным пьезоэффектами (возникновение поляризации диэлектрика под действием механических напряжений и наоборот, возникновение механических деформаций под действием электрического поля).

Часто электронные генераторы в своем составе используют кварцевые резонаторы, как элементы опорных колебаний, что приводит к повышению требований стабильности колебаний резонатора, отсюда возникает проблема сохранения этой стабильности за все время работы устройства.

В данной статье мы рассмотрим ряд методов решения этой проблемы исследованные и теоретически обобщенные за долгие годы научных трудов сотрудников кафедры «Радиотехнических устройств и систем диагностики» при Омском Государственном Техническом Университете.

Известно множество воздействующих факторов, на кварцевый резонатор и генератор (как устройство, в целом), которые приводят к снижению стабильности частоты. В наибольшей степени на стабильность генераторов, использующих кварцевые резонаторы, влияет изменение температуры окружающей среды. Температурные уходы частоты могут составлять и более. Существует два принципа борьбы с этим явлением: термостатирование (поддержания рабочей температуры устройства в узком диапазоне значений) и термокомпенсация (создание компенсирующего воздействия, в зависимости от изменения температуры, для управления генератором). Термостатирование обеспечивает лучшую температурную стабильность частоты по сравнению с термокомпенсацией, но существует и ряд недостатков такого способа борьбы с уходами частоты. Такие как: большая мощность, затрачиваемая на поддержание устройства в определенном температурном диапазоне, большое время готовности к работе генератора и большие габариты обусловленные наличием термостата. Для специальных применений часто от устройства требуются практически мгновенная готовность к использованию и, как можно меньшие массогабаритные показатели. Здесь предпочтительнее использование термокомпенсированных кварцевых генераторов.

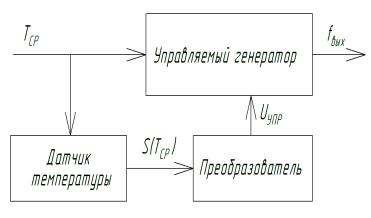
Термокомпенсированные кварцевые генераторы относят к объектам регулирование которых осуществляется «по воздействию». Часто с использованием математической модели объекта. Если математическая модель не учитывает каких-либо значащих факторов и внешних воздействий, то как бы точно она не была воспроизведена в устройстве достижение высокой стабильности будет невозможным. Структурная схема одной из возможных моделей реализации термокомпенсированного кварцевого генератора (ТККГ) приведена на рис. 1. Подобные модели исторически появились первыми и они учитывали только статические уходы частоты. Все действия по повышению стабильности частоты, при использовании данной модели, сводятся к повышению точности формирования управляющего воздействия. Учитывая все факторы, такие как: нелинейность ТЧХ, нелинейность зависимости частоты от управляющего напряжения, нелинейность термодатчиков и др., решение данной проблемы аналоговыми способами весьма сложная задача.

Рисунок 1. Структурная схема термокомпенсированного кварцевого генератора, учитывающего только статические уходы частоты

Остаточная раскомпенсация, при использовании данной модели в большинстве случаев велика и превышает влияние других воздействующих факторов. С появлением цифровых методов обработки проблема точности формирования управляющего воздействия была полностью решена и стали заметны влияния других воздействующих факторов. В частности, стала заметна зависимость частоты генератора от характера температурного процесса: при больших скоростях изменения температуры и резких температурных скачках нестабильность существенно возрастала.

Зависимость частоты кварцевого резонатора от характера температурного процесса давно известна. Л. Е. Ивлевым, В. П. Багаевым и Э. М. Фромбергом [1], еще в 1965г. для описания отклонений частоты кварцевого резонатора при нестационарных тепловых воздействиях было введено понятие температурно-динамического коэффициента частоты (ТДКЧ), определяемого как

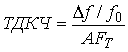, (1)

где А – амплитуда колебаний температуры на поверхности пьезоэлемета;

- частота синусоидальных колебаний температуры;

- вызванный этими колебаниями относительный уход частоты кварцевого резонатора.

ТДКЧ может быть относительно легко определен экспериментально, но он дает только числовую характеристику температурно-динамической чувствительности резонатора и предсказать форму ТЧХ в нестационарных тепловых воздействиях, используя известное значение ТДКЧ, очень сложно.

Теоретические исследования, проведенные еще в середине 70-х годов [2,3], позволили рассматривать температурно-динамические искажения ТЧХ резонатора как функцию от скорости изменения температуры. Результатом этих исследований стало выражение, описывающее ТЧХ кварцевого резонатора при воздействии линейно изменяющейся температуры

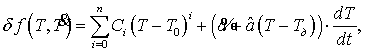(2)

где - температурно-динамический коэффициент сдвига ТЧХ;

- температурно-динамический коэффициент поворота ТЧХ;

- температура, относительно которой произведено разложение ТЧХ в ряд;

- температура, относительно которой определены динамические коэффициенты;

- первая производная температурного процесса.

Но исследования касались только термостатированных генераторов (у них стабильность частоты выше и влияние температурно–динамической зависимости частоты было замечено раньше). Попытка применить данную модель к описанию поведения ТККГ в динамическом температурном режиме показала, что эта модель не полностью соответствует реальным процессам и дает значительную погрешность, зависящую от конструктивного исполнения ТККГ. Влияние динамического температурного режима на частоту ТККГ впервые в мире подробно было исследовано сотрудниками кафедры «Радиотехнических устройств и систем диагностики» Омского Государственного Технического Университета [4,5,6], что позволило разработать ряд температурно-динамических моделей ТККГ.

Основная идея этих моделей заключается в формирование управляющего воздействия зависящего не от одной переменной (только температуры), а от двух (температуры и скорости ее изменения). Отсюда вытекает ряд проблем: 1. Проблема измерения скорости изменения температуры; 2. Проблема формирования двумерной функции управляющего воздействия. Ниже описан ряд моделей ТККГ, в которых решаются вышеизложенные проблемы.

Простым решением, которое позволяет обеспечить формирование сигнала, пропорционального скорости изменения температуры является использование для этой цели дифференцирующей RC-цепочки. В (А.с. №1109853/Косых А. В., Мухин В.Л., Опубл. в БИ № 31, 1984) [7] для целей динамической компенсации авторами предложена схема приведенная на рис.2.

Рисунок 2. Структурная схема динамической системы, которая использует простейший аналоговый канал компенсации

Параметры преобразующей (интегро-дифференцирующей) цепи для данной схемы подбираются таким образом, чтобы выровнять инерционность дополнительного датчика температуры с инерционностью основного канала (интегрирующая часть) и обеспечить приемлемую точность дифференцирования сигнала от этого датчика при наиболее вероятных скоростях изменения температуры.

Используя современные возможности вычислительных систем и САПР, по структурной схеме рис. 2 сотрудниками кафедры «Радиотехнических устройств и систем диагностики» Омского Государственного Технического Университета была создана и исследована модель в пакете Simulink. Результат моделирования приведен на рис. 3.

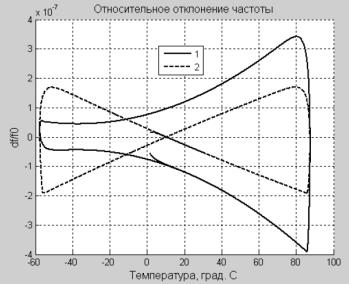
Рисунок 3. Динамическая ТЧХ полученная в результате моделирования схемы представленной на рис. 2 (кривая 1 – динамическая компенсация выключена; кривая 2, 3 – динамическая компенсация включена).

Анализируя полученный результат моделирования можно сказать, что система динамической компенсации, которая представлена на рис. 2 не приводит к глобальному снижению погрешности компенсации.

Статическое компенсирующее устройство в данной схеме может быть как аналоговым, так и цифровым. Недостатком такого решения явилось то, что не учитывается динамический «сдвиг» ТЧХ относительно сигнала термодатчика, обусловленный разностью тепловых инерционностей термодатчика и опорного резонатора.

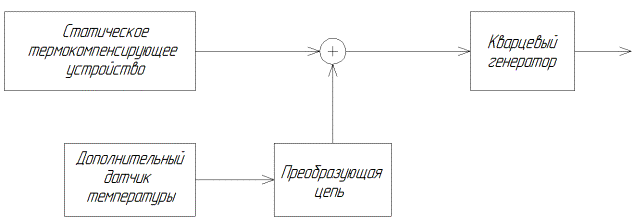
Авторы свидетельства № 1197035 Косых А. В., Ионов Б.П., Гросфельд Е.Г. [8] предложили решение этой проблемы рис. 4.

Рисунок 4. Структурная схема ТККГ с компенсирующим устройством, учитывающим разницу в тепловых инерционностях датчика температуры и резонатора

Сигнал датчика температуры, поступающий на функциональный преобразователь, получает аддитивную добавку, зависящую от скорости изменения температуры. Этим обеспечивается необходимый горизонтальный сдвиг ТЧХ. Недостатком данной схемы является то, что в ней не учитывается изменение динамической чувствительности системы термокомпенсации в интервале рабочих температур. Компенсация этой чувствительности аналоговыми является сложной задачей и сильно усложняет схему.

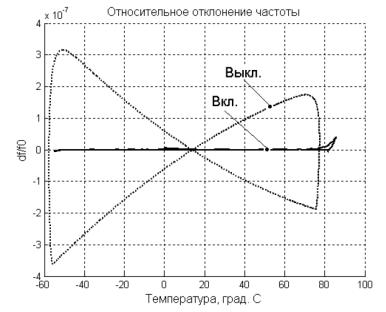
Рисунок 5. ТЧХ Генератора по А.С. №1197035 с включенной (2) и

выключенной (1) системой динамической термокомпенсации.

На рис. 5 представлены результаты моделирования схемы представленной на рис. 4. Моделирование проводили сотрудники кафедры «Радиотехнических устройств и систем диагностики» Омского Государственного Технического Университета. Как видно из графика (рис. 5) данный вариант также не обеспечивает требуемую точность компенсации во всем температурном интервале. Дальнейшее улучшение температурно-динамической чувствительности возможно только цифровыми способами.

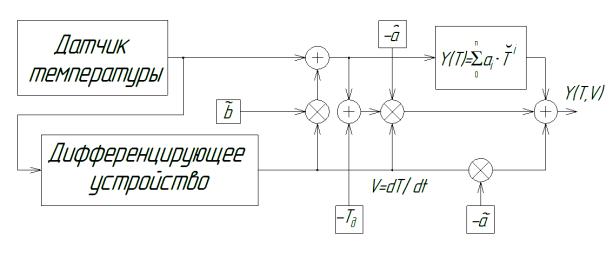
Рисунок 6. Блок-схема системы формирующей двумерную компенсирующую функцию

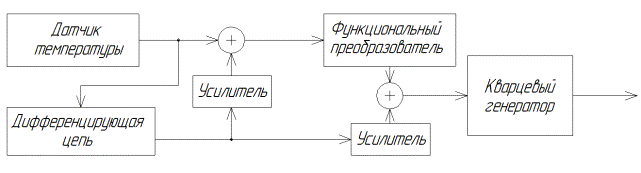
На рис. 6 представленна блок-схема системы сущностью которой является формирование компенсирующегно воздействия в форме, адекватной тепловой модели кварцевого генератора. Если в модели генератора есть блоки, осуществляющие аддитивные и мультипликативные сдвиги частоты, пропорциональные скорости изменения температуры, то в составе термокомпенсирующего устройства должны быть аналогичные блоки, но вызывающие сдвиги частоты противоположного знака. В данной схеме формируется температурное запаздывание между опорным резонатором и термодатчиком (горизонтальный сдвиг, пропорциональный коэффициенту ), а также вертикальный сдвиг и поворот ТЧХ (пропорциональные коэффициентам и соответственно). Для реализации такой схемы необходимо знать динамические коэффициенты , и . Методика определения этих коэффициентов известна.

Рисунок 7. Результаты моделирования в пакете Simulink системы компенсации формирующей двумерную компенсирующую функцию

Для оценки эффективности предложенного решения сотрудниками кафедры «Радиотехнических устройств и систем диагностики» Омского государственного технического университета проведено моделирование системы динамической термокомпенсации с использованием средств пакета Simulink. При моделировании опорный резонатор и термодатчик аппроксимировались инерционными звеньями первого порядка, а дифференцирование считалось идеальным. Результаты моделирования приведены на рис. 7.

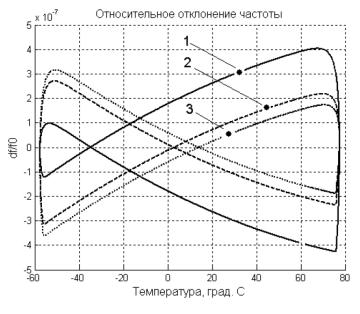
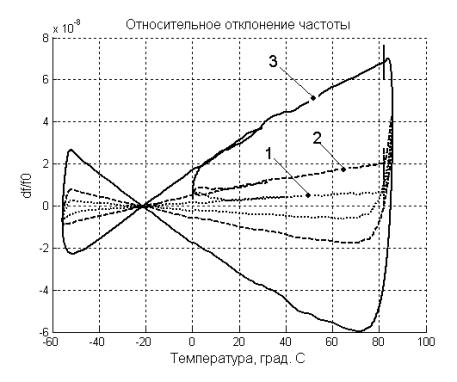
На Рис. 8 приведены результаты моделирования этой же системы но при различных точностях определения динамических коэффициентов 1% (1), 3% (2) и 10% (3).

Анализ полученных результатов показал, что если пренебречь высшими производными температурного процесса, то динамическая компенсация дает значительный выигрыш в стабильности. При этом точность определения динамических коэффициентов должна составлять 1 – 3 %

Рисунок 8. График отражающий влияние точности определения динамических коэффициентов

В данной статье рассмотрена лишь немногие системы и методы динамической термокомпенсации кварцевых генераторов. Представлены их достоинства и недостатки. Показан выигрыш в стабильности, который можно достичь путем введение в схему системы цифровых методов обработки сигналов.

Список литературы:

1. Ивлев Л. Е., Багаев В. П., Фромберг Э. М. О температурно-динамическом коэффициенте частоты кварцевых резонаторов. //Вопросы радиоэлектроники. Сер. 3. Детали и компоненты. 1965, вып. 2. с. 50 – 59.

2. Ballato A. Static and dynamic behavior of quartz resonators. //IEEE Trans. Sonics and Ultrasonics. – 1979, №4. – P. 299 – 306.

3. Holland R. Nomuniformly heated anisotropic plates. Pt. 1. // IEEE trans. sonics and ultrasonics. 1974, P. 171 – 178.

4. Косых А. В., Ионов Б. П. Температурно-динамическая модель и температурно-динамическая компенсация кварцевых генераторов. //Радиотехнические пьезоэлектронные устройства. - Омск, 1990. - С. 13-21.

5. Косых А. В., Ионов Б.П., Васильев А.М. Температурно-динамическая модель и температурно-динамическая компенсация кварцевых генераторов //Электронная техника. Сер. Радиодетали и радиокомпоненты. - 1991. - Вып. 4(85). - С.

6. Косых А. Температурно-динамическая модель термокомпенсирован-ного кварцевого генератора. //В сб. Тезисы докладов 1 Областной научно-технической конференции, Омск – 1983, с. 27.

7. А.с. № 1109853 (СССР) Устройство термокомпенсации кварцевого генератора. /Косых А. В., Мухин В.Л., Опубл. в БИ № 31, 1984.

8. А.с. № 1197035 (СССР) Устройство термокомпенсации кварцевого генератора. /Косых А. В., Ионов Б.П., Гросфельд Е.Г. Опубл. в БИ № 45, 1985.