Экономические науки/8. Математические методы в экономике

Меерсон А. Ю. – кандидат физико-математических наук, доцент

Черняев А. П. – доктор физико-математических наук, профессор

Российский экономический университет имени Г. В. Плеханова

Московский физико-технический институт (государственный университет)

Оптимальное управление для потребления макроэкономической модели Харрода–Домара с переменным коэффициентом приростной капиталоемкости

Дифференциальное уравнение модели Харрода-Домара с экзогенной динамикой потребления произвольного характера [1] имеет вид

,                                                                                                                       (1)

где  – время, – доход, равный сумме потребления  и инвестиций .  Основная предпосылка [2]:, где - коэффициент приростной капиталоемкости. В этом случае решение дифференциального уравнения (1) известно [3].

В настоящей работе предполагается, что , и в этом случае решение дифференциального уравнения (1) будет даваться формулой [4]

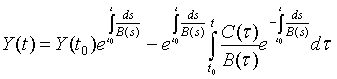.                                                                                                                       (2)

Задача оптимального управления ставится, как максимизация

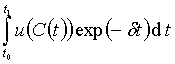,                                                                                                                                                     (3)

где u – функция полезности, а δ – коэффициент дисконтирования будущей полезности [5]. Выражая потребление из уравнения (1) подставляем его в (3):

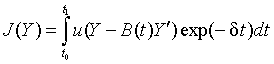.                                                                                                                       (4)

Нам достаточно рассмотреть разность J(Y + h) –J(Y), где h = h(t) – малое возмущение и показать неположительность этой разности.

На основании (4) можно записать

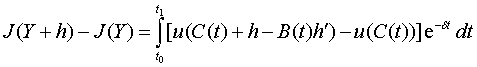.                                                                                                                       (5)

Используя формулу Тейлора с остаточным членом в форме Пеано, имеем

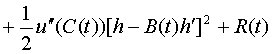,                                                                                                                                                     (6)

где

, при .                                                                                                                                                     (7)

Подставляя (6) и (7) в (5), получим

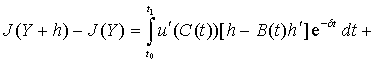
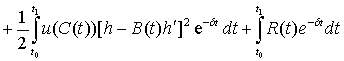.                                                                                                                                                     (8)

Пользуясь интегрированием по частям, мы можем записать

.

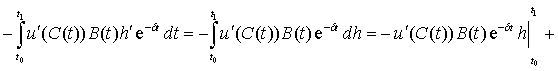
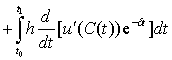Первое слагаемое правой части последнего равенства обращается в нуль, поскольку

.                                                                                                                                                     (9)

С учетом (9) предпоследнее равенство упрощается и будет иметь вид

.

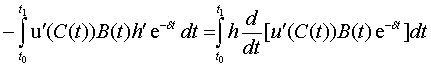Подставляя последнее в (8) будем иметь

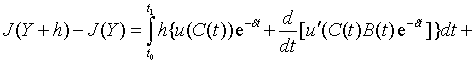
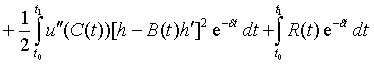.                                                                                                                                                     (10)

Используя основную лемму вариационного исчисления, получим

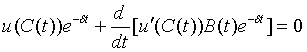.                                                                                                                                                     (11)

С учетом (11) представление (10) упрощается и будет иметь вид

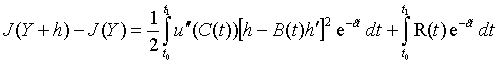.                                                                                                                       (12)

Заметим, что если в (12) h заменить на bh, где b = const, то, т. к. в этом случае h′ заменяется на βh′, можно записать

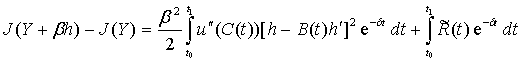,                                                                                                                       (13)

где – остаточный член из формул, аналогичных формулам (6), (7):

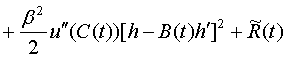,                                                                                                                       (14)

, при .                                                                                                                       (15)

Из (14) и (15) следует, что при фиксированном h и b ® 0 второе слагаемое правой части (13) есть бесконечно малая величина более высокого порядка, чем первое, если только первое слагаемое не равно нулю тождественно. Т. о., знак (13) полностью определяется отличным от тождественного нуля первым слагаемым правой части.

Полезность потребления оценивается монотонной функцией u(С), которая описывает относительное отвращение к риску по Эрроу-Пратту [5]. В силу этого u²(C(t)) £ 0, а значит первое слагаемое правой части равенства (12) неположительно. Следовательно, в силу (12) имеем

,

а значит (2) при (11) реализует максимум функционала (3), или, что то же самое (4)  при условиях (9).

Литература

1. Меерсон А. Ю., Черняев А.П. Точное решение макроэкономической модели  Харрода-Домара с экзогенной динамикой объема потребления произвольного характера // Известия Российского экономического университета им. Г.В.Плеханова. 2011, № 1. С. 142-147.

2. Замков О. О., Толстопятенко А. В., Черемных Ю. Н. Математические методы в экономике: Учебник. – М.: МГУ им. М. В. Ломоносова, Издательство «ДИС», 1998 – 368 с.

3. Меерсон А. Ю., Черняев А.П. Особенности рабочего режима макроэкономической модели  Харрода-Домара с показателем потребления растущим в постоянном темпе // Вестник МГУП. М.: МГУП, 2012, № 3. С. 188-192.

4. Меерсон А. Ю., Черняев А.П. Точное решение задачи Коши для дифференциального уравнения макроэкономической модели Харрода-Домара с переменным  коэффициентом приростной  капиталоемкости // Известия МГТУ «МАМИ» М.: МГТУ «МАМИ», 2013. Т. 3, серия 3 естественные науки. С. 112-114.

5. Гуриев С.М., Поспелов И.Г. Модель общего равновесия экономики переходного периода  // Математическое моделирование, 1994. Т. 6, №2. С. 3 - 21.

 

Российская экономическая академия им. Г.В. Плеханова, Москва

Московский физико-технический институт (государственный университет)

E-mail: allameerson@yandex.ru, chernyaev49@yandex.ru,  chernyaev1949@inbox.ru