ОЦЕНКА ПОГРЕШНОСТЕЙ ВЫЧИСЛЕНИЯ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК, ПРИ ИСПОЛЬЗОВАНИИ МЕТОДА СТОХАСТИЧЕСКОГО КОДИРОВАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ.

Г.Г. ГАЛУСТОВ

Приведено описание оценки погрешности вычисления математического ожидания случайных процессов, подвергнутых стохастическому кодированию с одноразрядным квантованием, при этом статистические характеристики кодированных процессов рассматриваются как эффективные признаки для решения задачи их распознавания

Успех решение задачи распознавания случайных сигналов (процессов) связан с выбором системы эффективных признаков, часто связанных нелинейной зависимостью с первичной системой признаков [1].

Использование нелинейного преобразования первичных признаковых пространств позволяет, с одной стороны, укрупнить описание классифицируемых сигналов, то есть отобразить исходное многомерное пространство признаков в одномерное пространство функционалов, с другой стороны – с применением в качестве функции преобразования функции распределения некоторого вспомогательного процесса – позволяет как бы “обобщить” или представить более компактно свойства всех сигналов одного класса.

Рассмотрим один из методов реализации алгоритма стохастического кодирования сигналов [2], ориентированного на классификацию сложных сигналов с непараметрической априорной неопределенностью, в котором, в общем случае реализовано нелинейное преобразование признаковых пространств.

Предположим, что анализируется с целью выделения признаков некоторый стационарный сигнал (процесс) , имеющий одномерную плотность вероятности .

Будем формировать процесс

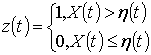, (1)

где - некоторый опорный процесс с плотностью вероятности .

В этом случае

. (2)

Так как при фиксированном значении ,

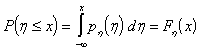, (3)

где - интегральный закон распределения случайной величины .

является функцией аргумента распределения сигнала, следовательно, можно сделать вывод, что интервал распределения опорного сигнала должен быть по крайней мере не меньше, чем интервал распределения анализируемого сигнала . На основании (3) и (2) запишем:

.

Известно [3], что

,

или окончательно запишем

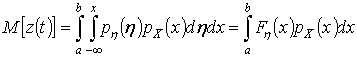, (4)

где - интервал распределения анализируемого сигнала .

В частном случае, когда

и значения процесса лежат также в интервале , то, а

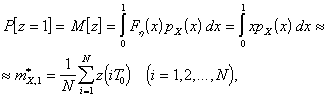(5)

где - интервал дискретизации процесса . Выражение (5) является оценкой первого начального момента. Для получения начального момента -го порядка, как это видно из (5), функция распределения опорного процесса должна быть , при этом

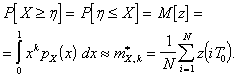(6)

Таким образом, в зависимости от вида функции распределения опорного сигнала, не изменяя структуры измерителя, мы можем получать оценки моментов различных порядков. Кроме того, можно синтезировать опорный процесс с таким распределением, чтобы получить заданное математическое ожидание при известной плотности распределения анализируемого сигнала .

Можно видеть, что использование оценок вида (6) в качестве аргумента векторов признаков классифицируемых процессов эффективно в случае классификации процессов с отличающимися одномерными плотностями вероятностей.

Особый интерес представляет связь статистических характеристик анализируемого процесса с процессом , полученным в результате сравнения с опорным распределением. При этом наибольший интерес представляет случай равномерного распределения опорного сигнала , так как в этом случае, в соответствии с (5), статистические характеристики процесса будут совпадать с начальными моментами его распределения.

Будем исходить из того, что анализируемый процесс является стационарным эргодическим и распределен в интервале . Тогда, полагая, что опорный процесс распределен равномерно в интервале , выражение (1) перепишем в виде

Составим ряд для дискретной случайной величины :

	0	1
P

Переходя к непрерывной случайной величине , можно сразу записать:

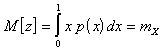; (7)

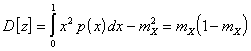. (8)

Для ошибки представления случайной величины в результате ее одноразрядного квантования также запишем ряд распределения, который будет иметь вид

P

Откуда при переходе к непрерывным случайным величинам имеем

. (9)

Таким образом, математическое ожидание ошибки в результате одноразрядного квантования независимо от вида распределения анализируемого процесса равно нулю.

Теперь определим дисперсию ошибки :

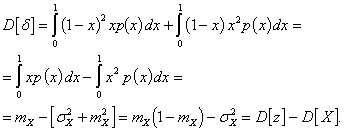(10)

Среднеквадратическое отклонение ошибки запишется как

. (11)

В соответствии с (5), математическое ожидание

;

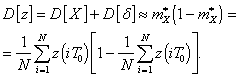(12)

Таким образом, дисперсия случайной величины может быть определена на основе выражения (12). Дисперсия оценки (5) может быть определена следующим образом:

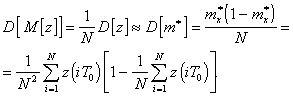(13)

Оценим теперь погрешности, вносимые стохастическим кодированием, для случая равномерного распределения опорного сигнала .

Оценка по стохастическому отображению представляет собой оценку вероятности события , () по его частоте в независимых опытах. Дисперсия оценки равна

.

Тогда с вероятностью можно утверждать, что величина погрешности определения по стохастическому отображению определяется выражением

.

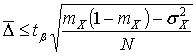Суммарная погрешность вычисления математического ожидания случайной функции по его стохастическому отображению равна [3]

, (14)

где - количество некоррелированных выборок из функции ;

-функция, обратная нормальной функции распределения [5].

В таблице 1 и на рисунке 1 приведены значения, графики для при различных и .

Таким образом, можно заключить, что при использовании метода стохастического кодирования возрастает дисперсия оценок измеряемых моментов, однако к положительным моментам можно отнести сокращение избыточности описания исходного процесса в раз [3],

где - разрядность представления двоичным кодом;

- порядок определяемой моментной функции процесса .

Например, если , , то .

Кроме того, при математической обработке процессов , полученных в результате применения метода стохастического кодирования, операции сложения и умножения сводятся к простейшим операциям - конъюнкции и счету импульсов. Это позволяет строить относительно простые вероятностные процессоры для статистической обработки данных с целью выделения эффективных признаков.

Таблица 1

	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
100	8,6	13,1	15	15,9	16,2	15,9	15	13,1	8,6
400	4,3	6,6	7,5	7,95	8,1	7,95	7,5	6,6	4,3
900	2,87	4,38	4,99	5,3	5,4	5,3	4,99	4,38	2,87
4900	1,23	1,88	2,14	2,27	2,31	2,27	2,14	1,88	1,23
10000	0,86	1,3	1,5	1,59	1,62	1,59	1,5	1,3	0,86

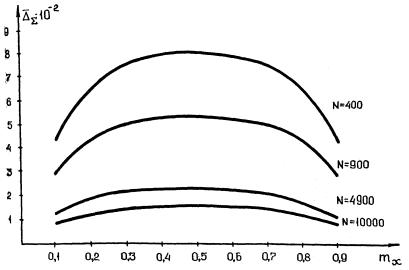
Рисунок 1. Зависимость погрешности от значений и .

Библиографический список

1. Фукунага К. Введение в статистическую теорию распознавания образов. Пер. с англ.-М.: Наука. 1979, 368с.

2.Г.Г. Галустов, В.Г. Цымбал, М.В. Михалев. Принятие решений в условиях неопределенности. М.: Радио и связь, 2001. 196 с.

3.В.С. Гладкий. Вероятностные вычислительные модели. М.: Наука, 1973. 298с.