К.ф.-м.н. Яковлева Е.Н., Матошина В.С.

Лесосибирский педагогический институт – филиал Сибирского федерального университета, Россия

СВОЙСТВА КОЛЕЦ Z[i] И Z[ɷ] .

Кольцо R называется евклидовой областью, если существует какая-либо функция λ из множества его ненулевых элементов в множество {0, 1, 2, 3,…}, обладающая следующим свойством: для любых a,b ϵ R, b ≠ 0, найдутся такие c,d ϵ R, что a = cb+d и либо d = 0, либо λ(d) < λ(b).

Пусть i =, и рассмотрим множество комплексных чисел Z[i], определенное как {a+bi | a,b ϵ Z}.Это множество замкнуто относительно сложения и вычитания. Кроме того, если a+bi ϵ Z[i], c+di ϵ Z[i], то (a + bi)(c + di) = ac + adi + bci + bdi² = (ac - bd) + (ad + bc)i ϵ Z[i]. Таким образом, Z[i] замкнуто относительно умножения и является кольцом. Так как Z[i] содержится в поле комплексных чисел, оно является областью целостности.

Предложение 1. Z[i] – евклидова область.

Доказательство. Для a + bi ϵ Z[i] положим λ(a + bi) =.

Пусть α = a+bi и γ = c+di, и предположим, что γ ≠ 0. Тогда α/γ = r + si, где r и s – вещественные числа (они на самом деле рациональны). Выберем целые числа m, n ϵ Z[i] так, что |r – m| ≤ 1/2 и |s – n| ≤ 1/2 . Положим δ=m+ni. Тогда δ ϵ Z[i] и λ((α/γ) – δ) = ≤ 1/4+ 1/4=1/2. Пусть ρ = α- γδ. Тогда ρ ϵ Z[i] и либо ρ = 0, либо

λ(ρ) = λ(γ ((α/γ) – δ)) = λ(γ) λ ((α/γ) – δ) ≤ (1/2) λ(γ) < λ(γ).

Отсюда следует, что функция λ превращает Z[i] в евклидову область.

Кольцо Z[i] называется кольцом гауссовых целых чисел в честь К.Ф.Гаусса, который первый детально изучил его арифметические свойства.

Числа ±1, ±i являются корнями уравнения =1 над полем комплексных чисел.

Рассмотрим уравнение =1. Так как – 1 = (x –1)(), то корнями этого уравнения будут 1, (-1 ± i)/2. Пусть ɷ = (-1 + i)/2. Тогда нетрудно проверить, что ɷ= (-1- i)/2 и что 1 + ɷ + ɷ= 0.

Рассмотрим множество Z[ɷ] ={a + bɷ | a,b ϵ Z}. Оно замкнуто относительно сложения и вычитания. Кроме того, (a + bɷ)(c + dɷ) =ac +(ad+ + bc)ɷ + bd ɷ= (ac – bd) + (ad + bc – bd)ɷ. Таким образом, Z[ɷ] является кольцом. Опять ввиду того, что Z[ɷ] – подмножество поля комплексных чисел, оно будет областью целостности.

Заметим, что Z[ɷ] замкнуто относительно комплексного сопряжения. Действительно, мы видим, что ϖ = ɷ. Таким образом, если α = a+bɷ ϵ Z[ɷ], то ᾱ =a + b ϖ = a + bɷ= a + b(-1 – ɷ) = (a – b) – bɷ ϵ Z[ɷ].

Предложение 2. Z [ɷ] – евклидова область.

Доказательство. Для α = a+bɷ ϵ Z[ɷ] определим λ(α) = . Простое вычисление показывает, что λ(α) = α. Действительно, α = (a + +bɷ)( a + b) = (a + bɷ)(a – b – bɷ) = a(a – b) + b(a – b)ɷ – abɷ – b²ɷ² =

= a²– ab +abɷ – b²ɷ – abɷ – b²(-1– ɷ) = a²– ab– b²ɷ + b² + b²ɷ = a²– ab + b².

Пусть теперь α, β ϵ Z[ɷ], и предположим, что β ≠ 0. Тогда α/β =α / β= = r +sɷ, где r и s – рациональные числа. Мы использовали тот факт, что β = =λ(β) – положительное целое число и что α ϵ Z[ɷ], так как α и ϵ Z[ɷ].

Выберем целые числа m и n так, чтобы |r – m| ≤ 1/2 и |s – n| ≤1/2, и пусть γ = m + nɷ.

Тогда λ((α/ β) - γ) = ≤ 1/4+ 1/4+1/4 < 1.

Пусть ρ = α – γβ. Тогда либо ρ = 0, либо λ(ρ) = λ(β((α/β) – γ)) < λ(β).

Докажем ряд свойств колец Z[i] и Z[ɷ].

Упражнение 1. Доказать, что 2 делится на (1 + i)² в Z[i].

Решение. Если a,b ϵ R, b ≠ 0, где R – некоторое кольцо, то говорят, что a делится на b, если a = bc для некоторого c ϵ R. Число 2 можно представить в виде 2 = (1 + i)(1 – i). Тогда получим .

Так как число – i принадлежит кольцу Z[i], то делимость доказана.

Упражнение 2. Для α = a+bi ϵ Z[i] определено λ(a + bi) =. Из свойств функции λ вывести тождество (a²+ b²)(c² + d²) = (ac – bd)²+ (ad + bc)².

Решение. Рассмотрим два числа из кольца Z[i]: α = a+bi и β = c+di.

Так как λ(α ) = a²+ b² , λ(β) = c² + d², то возникает предположение, что функция λ обладает свойством мультипликативности, т.е. λ(α× β) = λ(α ) × λ(β).

Действительно, λ(α ) × λ(β) = λ(a + bi) λ(c+ di) = (a²+ b²)(c² + d²) = a²c²+ + b²c² + a²d² + b²d².

С другой стороны, λ(α× β) = λ((a + bi) × (c+di)) =λ(ac –bd+ (ad + bc)i) =

= (ac – bd)²+ (ad + bc)² = a²c²- 2acbd + b²d² + a²d² +2adbc + b²c² = a²c²+ b²c² + +a²d² + b²d². Таким образом, свойство доказано, тождество следует из свойства.

Упражнение 3. Показать, что α ϵ Z[i] является единицей тогда и только тогда, когда λ(α) = 1. Получить отсюда, что 1, -1, i, –i – единственные единицы в кольце Z[i].

Решение. Элемент α из кольца Z[i] называется единицей, если он делит 1. Элемент α из кольца Z[i] делит 1, если 1 = α×с, где с ϵ Z[i].

Пусть α = a+bi и λ(α) = 1, тогда можем записать: (a + bi)(a – bi) = a² + +b² = 1, где a – bi ϵ Z[i]. Следовательно, α – единица.

Пусть теперь α – единица кольца Z[i], докажем, что λ(α) = 1.

Так как α – единица, то существует элемент с ϵ Z[i], такой что 1 = α×с.

λ(1) = 1, следовательно λ(α×с) = 1= λ(α)× λ (с). Так как λ(α) и λ(с) – неотрицательные целые числа, то λ(α) = λ (с) = 1.

Теперь найдем все единицы в кольце Z[i]. Пусть (a + bi)(a – bi) = 1, тогда ac –bd + (ad + bc)i = 1. Отсюда получаем систему уравнений:

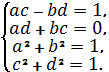
Решая систему, получим a = c, b(b + d) = 0.

1. Пусть b = 0. Тогда a² = 1, a = ± 1, ad = 0, d = 0.

2. Если (b + d) = 0, то b = -d. Если b ¹ 0, получаем a = 0 и b = ± 1.

Таким образом, получаем: в первом случае α = 1 или α = -1. Во втором случае α = i или α = -i. Этими числами исчерпываются все единицы кольца.

Упражнение 4. Показать, что 3 делится на (1 – ɷ)² в кольце Z[ɷ].

Решение. Рассмотрим равенство (1 – ɷ)²(1 – ɷ) = (1 – ɷ)³ = 1 – 3ɷ + +3ɷ²– 1 = 3ɷ²–3ɷ =3ɷ(ɷ – 1). Отсюда получаем

В итоге получили 3 = причем - ɷ² ϵ Z[ɷ]. Значит 3 делится на (1 – ɷ)².

Упражнение 5. Для α = a+bɷ ϵ Z[ɷ] определено λ(α) = . Показать, что α является единицей тогда и только тогда, когда λ(α) = 1.

Решение. Пусть λ(α) = 1, докажем, что α является единицей Z[ɷ]. Для этого рассмотрим произведение (a+bɷ)(a+bɷ²) = a²+abɷ + abɷ²+ b²ɷ³ = =a²+abɷ + abɷ² + b²= a² +abɷ + abɷ²+ b²ɷ³ = a²+abɷ + abɷ²+ b² +ab – ab = =( a² – ab + b²) + (abɷ + abɷ²+ ab) = 1 + ab(1 + ɷ + ɷ) = 1.

Таким образом, (a + bɷ)(a + bɷ²) = 1. Так как a + bɷ= a + b(-1 – ɷ) = =(a – b) – bɷ, то a+bɷ² ϵ Z[ɷ]. Следовательно, α является единицей Z[ɷ].

Обратно. Пусть α является единицей, докажем, что λ(α) = 1.

Предварительно докажем, свойство λ(α× β) = λ(α ) × λ(β). Действительно, так как λ(α) = α то λ(α× β) = αβ = = λ(α) λ(β).

Так как α является единицей, то существует элемент β ϵ Z[ɷ], такой, что α× β = 1. Так как λ(1) =1, то λ(α× β) = λ(α ) × λ(β) = 1. Так как λ(α) и λ(β) – неотрицательные целые числа, то λ(α) = λ (β) = 1. Утверждение доказано.

Литература:

1. Айерлэнд К., Роузен М. Классическое введение в современную теорию чисел. М.: Мир, 1987.