Математика/5. Математическое моделирование

студ. Полищук В. Ю.

НТУУ «Киевский политехнический институт», Украина

Выбор стратегии оптимального перестрахования

 Задача оптимального перестрахования является актуальной для страховой компании, поскольку ее решение дает возможность повысить эффективность деятельности страховщика за счет повышения финансовой устойчивости компании. При разработке программы перестрахования для риска нужно найти оптимальное решение – какую форму перестрахования выбрать и на сколько перестраховывать. Иными словами, возникает несколько вопросов, и многие факторы должны быть рассмотрены: бизнес-модель, финансовая устойчивость и неприятие риска, рыночные условия и возможности.

Поиск оптимальных в разных смыслах стратегий перестрахования является важным направлением исследований в течение нескольких десятилетий и не потерял своей значимости до сих пор, а потому ему посвящено множество работ. В работах [1 – 3] показано, что stop-loss перестрахование обеспечивает минимальную дисперсию выплат и максимальный ожидаемый доход страховой компании по сравнению с любыми другими видами перестрахования (функциями распределения убытка) той же стоимости при условии, что премия перестраховочной компании определяется из принципа ожидаемого значения (принципа эквивалентности). Позже различные исследования появились в пользу других видов перестрахования. В 1977 году Beard и др. [4] доказали, что квотное перестрахование является оптимальным в том смысле, что это самый дешевый способ ограничить дисперсию нераспределенной риска, если коэффициент нагрузки возрастает с увеличением дисперсии перестраховочной части ущерба.

В исследовании предложено поиск оптимальной стратегии перестрахования с учетом изменения финансового состояния и отношения к риску страховой компании. Для этого оптимальная форма перестрахования и ее параметр ищутся в условиях ограничений на капитал, которым готова рискнуть страховая компания и на доход, который она ожидает получить от заданного страхового портфеля.

Стратегия поиска оптимального перестрахования состоит из следующих этапов:

1) нахождение распределения совокупного убытка портфеля;

2) оценка значений, отображающих риск и доход портфеля от параметров перестрахования;

3) поиск наилучшей формы перестрахования и оптимального параметра в соответствии с выбранным критерием.

Для нахождения распределения совокупного убытка портфеля используется коллективная модель риска. Для моделирования распределения размера убытка используются следующие распределения:

1) логнормальное распределение (параметры ):

,;

2) распределение Вейбулла (параметры ):

Количество убытков страхового портфеля соответствует пуассоновскому закону распределения с параметром

В качестве исследуемых форм перестрахования взяты:

1) квотное перестрахование:

;

2) перестрахование эксцендента убытка:

;

3) перестрахование стоп-лосс:

;

где первое слагаемое – собственное удержание страховика, а второе – часть убытка, которая передается перестраховщику.

Для оценки дохода и риска используются следующие характеристики:

– премии по портфелю;

– ожидаемая прибыль;

- максимально возможный ущерб, который может произойти с заданной вероятностью;

– собственный капитал компании под риском;

– отношение ожидаемой прибыли к капиталу под риском.

Максимизация учитывает как максимизацию ожидаемого дохода так и минимизацию . Поэтому именно используем в качестве критерия для нахождения оптимального параметра перестрахования. Заметим, что параметры различаются для различных форм перестрахования, но сравнив их значение с , можем выбрать лучшую форму перестрахования. Соответственно оптимальным перестрахованием есть такая программа – форма перестрахования и ее параметр, в которой показатель максимальный.

Схематично модель поиска оптимального перестрахования изображена на рис. 1. Модель состоит из трех основных модулей: модуля убытков, модуля перестрахования, модуля результатов.

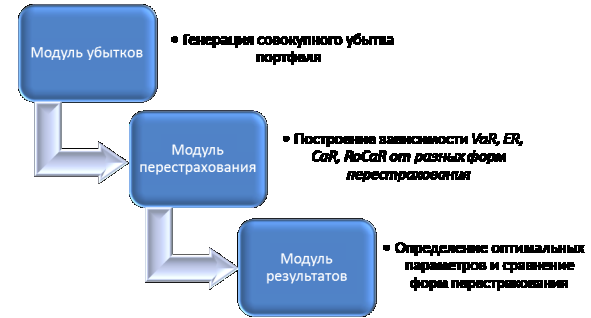
Рис.1 Модель поиска оптимального перестрахования

При нахождении величины оптимального перестрахования учтена зависимость коэффициента нагрузки от формы перестрахования.

В специальной литературе не найдено варианта решения этой задачи численными методами; аналитические методы не дают инструментария для их использования в повседневной практике. Коэффициент нагрузки учитывался при расчете премии, но при сравнении различных форм перестрахования использован одинаковый коэффициент.

В реальных условиях коэффициент нагрузки зависит от формы перестрахования. Соответственно, выполнено исследование на предмет зависимости оптимальной формы перестрахования от переменного коэффициента нагрузки.

Применив данную стратегию поиска оптимального перестрахования для страхового портфеля каско, были получены следующие результаты: при отсутствии данного условия (различные коэффициенты нагрузки) оптимальной формой перестрахования stop-loss, с чем согласуется выполненное исследование. Но при учете переменного коэффициента нагрузки при определенных значениях капитала, которым готова рискнуть страховая компания stop-loss уступил место оптимальной другим формам перестрахования.

Литература:

1. Borch K. “The utility concept applied to the theory of insurance”, ASTIN Bulletin 1, 1961, p. 245-255.

2. Kahn P. “Some remarks on a recent paper by Borch”, ASTIN Bulletin 1, 1961, p. 265-272.

3. Arrow K. “Uncertainty and the welfare of medical care”, American Economic Review 53, 1963, p. 941-973.

4. Beard, R. E., Pentikainen, T. and Pesonen, E., 1977. Risk Theory, 2^nd ed., Chapman and Hall, London.