Математика/4. Прикладная математика

Бабков А.С.

Юго-Западный государственный университет, Россия

Формирование информативного признакового множества

В последнее время наблюдается интенсивное внедрение компьютерных технологий, методов искусственного интеллекта, различных статистических подходов в решение задач разработки автоматизированных систем поддержки принятия решений в медицине в области ранней диагностики различных заболеваний на этапе первичного обследования пациента [1,2,4].

Одним из наиболее распространенным подходом к построению диагностических систем является теория распознавания образов [5].

Для оптимального построения диагностических систем выбираются множества признаков, характеризующие альтернативные классы. При построении систем дифференциальной диагностики [6] достаточно на каждом этапе бинарного дерева осуществлять соотнесение объекта к одному из альтернативных классов w₀ и w₁.

Рассмотрим, например формирование информативного признакового множества доклинической диагностики возможности возникновения или наличия рака желудка по результатам общего анализа крови [7] , как соединительной ткани, «обладающей» информацией о всех происходящих в организме системных изменениях, к которым, безусловно, относится развитие онкологических заболеваний.

Будем рассматривать следующие классы людей: возможно болеющих раком желудка (класс w₀₎ и не страдающими указанным заболеванием (класс w₁) .

Для выбора множества признаков, обладающих необходимой степенью классификационных возможностей, предлагается следующая методика.

Пусть заданно некоторое исходное множество показателей {Pr}_g , где g – исходное количество признаков, g≠0. Требуется сформировать множество признаков {Prо}_gо , где gо – количество признаков, 1≤go≤g, обладающее наибольшими классификационными возможностями. Из разницы между множествами {Pr}_g и {Prо_э}_gоэ возникает задача отбора признаков, обладающими наибольшими классификационными возможностями, апробированными, статистически доказуемыми, формализованными методами.

Для этого необходимо иметь по каждому из альтернативных классов некоторые множества численных данных. Речь идет, в данном случае, о разведочном анализе, то с учетом их априорной принадлежности к нормальному закону распределения.

Для отбора признаков используются значения коэффициентов Стьюдента различий между двумя выборками на определенном уровне ошибки первого рода. При решении диагностических задач в медицине численное значение указанной ошибки, как правило, принимается в диапазоне [0.05; 0.1] – конкретное значение определяется из предъявляемых требований к качеству диагностической системы и объему выборок.

Наряду с регистрируемыми частными показателями общего анализа крови (множеством {Х}) для повышения качества доклинической диагностики рака желудка формируется дополнительное множество интегральных показателей (множество {Y}), расчет элементов которого проводится по формуле (1).

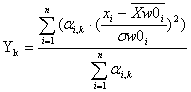(1),

_{. –} интегральный показатель, - индекс интегрального показателя, _- значение i-го частного показателя крови у пациента, - соответственно, модальное значение (в случае нормального распределения совпадает с математическим ожиданием и средним значениями) и средне-квадратичное отклонение (СКО) i-го частного показателя крови, полученное на обучающей выборке для класса «здоровые», - весовые коэффициенты, определяющие информационный вклад показателя в формирование интегрального показателя .

Весовые коэффициенты в указанной формуле предлагается определять следующими способами:

1. Путем назначения экспертами, исходя из личного опыта и анализа информационных медицинских источников.

2. Автоматически – на основе применения определенного статистически обоснованного математического аппарата.

3. Смешанным способом.

Во всех трех способах необходимо иметь единые шкалы измерений и ограничений. Принимаем ограничения:

(2),

где n – количество частных показателей множества {Х}, k – номер интегрального показателя Y (k≥0).

Предлагается следующая методика определения рассматриваемых информационных коэффициентов (действительна только при наличии двух альтернативных классов):

1. Регистрируются для каждого альтернативного класса значения элементов множеств (где n –количество частных показателей (крови)).

2. По значениям коэффициента Стьюдента на заданном уровне значимости (ошибки первого рода) осуществляется селекция показателей с предположительно незначительными классификационными возможностями. В результате селекции для дальнейшего формирования информативного признакового пространства используется множество , где m_x – количество показателей крови, оставшихся после селекции.

3. По каждому показателю (признаку) вычисляются коэффициенты Стьюдента различий между двумя альтернативными классами – формируется множество , элементами которого () являются значения коэффициентов Стьюдента.

4. Элементы полученного множества ранжируются (по убыванию или возрастанию). Строится диаграмма значений полученного ряда, по которой исследователь определяет необходимое количество (m_y ,m_y≤m_x) и «состав» интегральных показателей путем выделения кластеров близких (по некоторой мере исследователя) значений ранжированных коэффициентов Стьюдента.

5. Каждому кластеру k (k=1,…,m_y) ставится в соответствие определенный интегральный показатель Y_k и соответствующее подмножество частных показателей . Формула (2) модифицируется в формулу:

(3).

6. Для каждого интегрального показателя Y_k с учетом вычисленных в п.2 значений коэффициентов Стьюдента и выделенных в п.3 кластеров определяются значения соответствующих весовых коэффициентов в (3) по формуле:

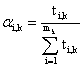(4).

Полученные величины весовых коэффициентов позволяют в дальнейшем формировать значения множества интегральных показателей {Y}.

Таким образом, множество информативных признаков {Pr}_g для решения задачи обучения системы классификации (диагностики) формируется по формуле:

(5),

где - соответственно: множество отселектированных частных показателей по изложенной выше методике, множество отселектированных интегральных показателей, множество отобранных экспертом показателей; элементами всех множеств являются «идентификаторы» показателей.

По результатам анализа показателей крови больных с клинически подтвержденным диагнозом «рак желудка» для формулы (1) получены следующее множество весовых коэффициентов {0;0;0.44;0;0;0;0;0;0.56}. (Рассматривалось следующее множество частных показателей крови {X} ={ Х₁ - эритроциты, Х₂- гемоглобин, Х₃ - цветовой показатель, Х₄ - лейкоциты, Х₅ - эозинофилы, Х₆ -палоочкоядерные, Х₇ - сегментоядерные, Х₈ - лимфоциты, Х₉-моноциты, Х₁₀ - СОЭ}

Таким образом, согласно (1) получаем следующую формулу для вычисления интегрального показателя:

(6)

Назовем этот показатель Y - «ЭрГеМо» - это обуславливается тем, что в него входит «Цветовой показатель» и «Моноциты», а первый, в свою очередь рассчитывается исходя из значений показателей: «Эритроциты» и «Гемоглобин».

Таким образом, в множество информативных признаков (с точки зрения их классификационных возможностей) включаются: частные показатели крови - «Эритроциты», «Гемоглабин», «Цветовой показатель», «Моноциты», «СОЭ» и интегральный показатель «ЭрГеМо».

Проверка диагностических возможностей выявленных показателей на контрольной выборке показала классификацию с ошибкой первого рода p<0.1.

Таким образом, предлагаемый подход формировании информативного признакового, основанный на статистических критериях способен адекватно реализовать поставленную задачу.

Литература:

1. Гланц С. Медико-биологическая статистика. Пер. с англ. – М.: Практика, 1999. - 259 с.

2. Котов Ю.Б. Новые математические подходы к задачам медицинской диагностики. - М.: Единоториал УРСС, 2004. - 328 с.

3. Клюшин Д., Петунин Ю. Доказательная медицина. Применение статистических методов. - Вильянс: Диалектика, 2008. - 320 с.

4. Омельченко В., Демидова А. Математика. Компьютерные технологии в медицине. – Ростов-на-Дону: Феникс, 2010. - 592 с.

5. Вапник В., Червоненкис А. Теория распознавания образов. – М.: Наука, 1974. - 416 с.

6. Дифференциальная диагностика внутренних болезней / ред. В.В. Щекотова. - Ростов-на-Дону: Феникс, 2007. - 592 с.

7. Кровь – индикатор стояния организма и его систем / ред. Р.В. Ставицкой. – М.: МНПИ, 1999. – 160 с.