Лазаренко
А.С., Пуляева М.Д.
Бердянський
державний педагогічний університет
УСТОЙЧИВОСТЬ СТРУИ ЖИДКОСТИ ПРИ
СВОБОДНОМ ИСТЕЧЕНИИ ИЗ КРУГЛОГО ОТВЕРСТИЯ
Аннотация. В работе рассматривается процесс свободного вертикального истечения струи
идеальной жидкости из круглого отверстия. Проведен расчет профиля вертикального
сечения струи. Получены функциональные зависимости площади свободной
поверхности струи, объёма и массы струи от длины струи и времени. В рамках
закона сохранения энергии получен критерий устойчивости течения струи.
При наблюдении
вертикальной струи реальной жидкости достаточно легко заметить, что, начиная с
определённой длины струи, устойчивость течения нарушается. Струя утрачивает
неразрывность и превращается в последовательность капель. Принято считать, что происходит
переход от ламинарного течения к турбулентному. Количественно такой переход
описывается как превышение значением числа Рейнольдса для струи
соответствующего критического значения.
Число Рейнольдса
определяется соотношением:
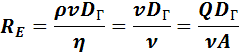
где
·
![]() —
плотность среды, кг/м3;
—
плотность среды, кг/м3;
·
![]() —
характерная скорость, м/с;
—
характерная скорость, м/с;
·
![]() —
гидравлический диаметр, м;
—
гидравлический диаметр, м;
·
![]() —
динамическая вязкость среды, Н·с/м2;
—
динамическая вязкость среды, Н·с/м2;
·
![]() —
кинематическая вязкость среды, м2/с;
—
кинематическая вязкость среды, м2/с;
·
![]() —
объёмная скорость потока;
—
объёмная скорость потока;
·
![]() —
площадь сечения струи.
—
площадь сечения струи.
Рассмотрим процесс
образования струи в рамках модели идеальной жидкости. Выясним, возможно ли нарушение
устойчивости без возникновения турбулентности.
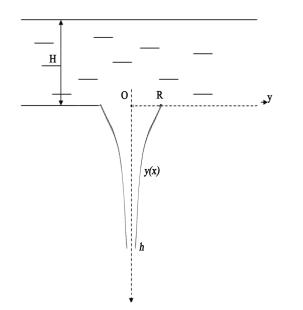 Пусть струя вытекает из круглого
отверстия радиуса R,
проделанного в плоском горизонтальном дне неограниченного резервуара с
постоянным уровнем жидкости. Уровень жидкости в резервуаре сравним с размерами
отверстия (Рис.1).
Пусть струя вытекает из круглого
отверстия радиуса R,
проделанного в плоском горизонтальном дне неограниченного резервуара с
постоянным уровнем жидкости. Уровень жидкости в резервуаре сравним с размерами
отверстия (Рис.1).
Рис. 1 Модель
образования свободной струи.
Такой выбор резервуара
и уровня жидкости в нём обеспечивает вытекание струи с нулевой начальной
скоростью, поскольку давление уровня жидкости уравновешивается обратным
лапласовским давлением в начальной стадии формирования струи (Рис.2).
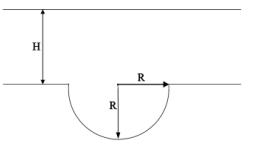
Рис. 2 Начальная
стадия образования струи
![]() ;
; ![]()
где ρ- плотность
жидкости4; g - ускорение свободного
падения; Н - требуемый уровень жидкостив резервуаре; R - радиус отверстия; s - коэфициент поверхностного натяжения жидкости.
Определим профиль плоского
вертикального сечения струи в плоскости (XOY).
Считая, что истечение
струи происходит под действием силы тяжести с нулевой начальной скоростью
получаем следующую зависимость скорости течения в струе от координаты x:
![]() (1)
(1)
Используя условие
неразрывности струи:
S(x)v(x)=const,
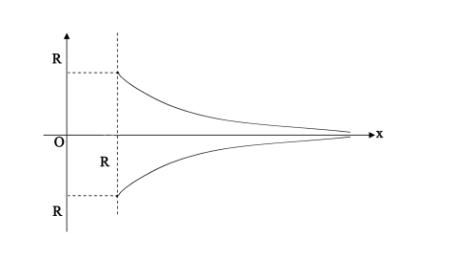 где S(x) –
зависимость площади поперечного сечения струи от координаты х., получаем
функциональную зависимость формы профиля вертикального сечения струи от
координаты х (Рис.3):
где S(x) –
зависимость площади поперечного сечения струи от координаты х., получаем
функциональную зависимость формы профиля вертикального сечения струи от
координаты х (Рис.3):
Рис. 3. Форма профиля вертикального сечения свободной
струи идеальной жидкости.
![]() (2)
(2)
Анализ выражения (2)
позволяет сделать вывод о том, что струя должна оканчиваться закруглением,
радиус которого определяется выражением:
![]() (3)
(3)
где h - длина
струи.
Рассчитывая площадь
поверхности струи в зависимости от её длины, получаем:
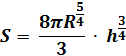 (4)
(4)
Зависимость площади
боковой поверхности от времени даётся выражением:
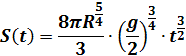 (5)
(5)
Следующие выражения
дают зависимости объёма и массы струи от её длины и времени:
![]() ;
(6)
;
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
При увеличении длины
струи работа силы тяжести расходуется на увеличение скорости течения и энергию
образования свободной поверхности струи. Если при элементарном приращении длины
на dx работа силы тяжести превысит
суммарное приращение кинетической и поверхностной энергии, то устойчивость
струи будет нарушаться за счёт образования дополнительной свободной
поверхности, то есть разбивания струи на отдельные капли.
Таким образом
критерий нарушения устойчивости течения можно записать в виде выражения:
![]() (10)
(10)
После подстановок и
преобразований получаем для критического значения длины струи:
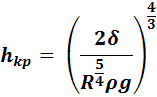 (11)
(11)
Таким образом, если
длина свободной вертикальной струи идеальной жидкости превысит критическое
значение, определяемое выражением (11), струя утратит устойчивость и разобьётся
на отдельные капли в силу выполнения закона сохранения энергии.
Литература
1. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. —5-е изд., — 2006. — Т. VI. Гидродинамика. —
736 с.
2. Лойцянский Л.Г. Механика жидкости и газ.. – М.: Дрофа, 2003. – 840 с.
3. Шлихтинг Г. Теория пограничного слоя. – М.: Наука, 1974. – 711 с.