Физика/7. Оптика

Костина Н. А., Одаренко Е. Н.

Харьковский национальный университет радиоэлектроники, Украина

МОДЕЛИРОВАНИЕ ДИФРАКЦИИ ПЛОСКОЙ ВОЛНЫ НА ЦИЛИНДРИЧЕСКОЙ ПОВЕРХНОСТИ С ПОКРЫТИЕМ

Создание и совершенствование современных приборов микроволнового и оптического диапазонов во многом связано с применением новых материалов. Результаты экспериментальных и теоретических исследований искусственных сред с отрицательными значениями материальных параметров (метаматериалы) свидетельствуют о перспективности их применения для разработки новых устройств с необычными электродинамическими характеристиками [1].

На основе применения метаматериалов создаются средства для маскировки объектов (cloaking), формирования уникальных линз, волноводов и высокодобротных резонаторов [2]. Основой для моделирования взаимодействия электромагнитных сигналов с такими объектами служит решение базовых задач дифракции плоских волн на элементарных геометрических объектах — отверстиях, цилиндрах, сферах и т. д.

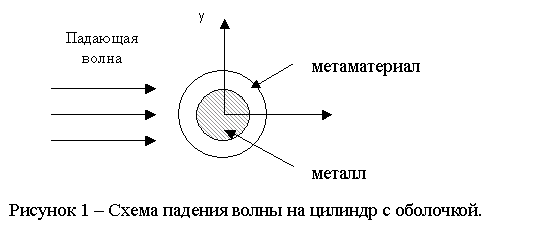
В данной работе рассматривается дифракция плоской монохроматической волны на металлическом цилиндре со слоем, материальные параметры которого могут иметь как положительные, так и отрицательные значения. Основное внимание уделено разработке средств визуализации распределения поля внутри оболочки и в области пространства вблизи цилиндра. На рис. 1 представлена схема падения волны на исследуемую структуру. Предполагается что вектор напряженности электрического поля направлен вдоль продольной оси цилиндра.

Для решения задачи были использованы представления полей через цилиндрические функции и граничные условия для раздела сред воздух-метаматериал и метаматериал-металл. В результате получили систему уравнений для определения неизвестных коэффициентов разложения. Для решения системы уравнений использовался метод Крамера. Ниже приведены выражения для определителей, которые использовались при составлении расчетного проекта в системе компьютерной алгебры:

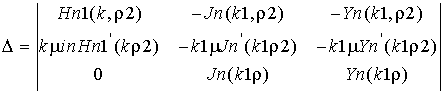
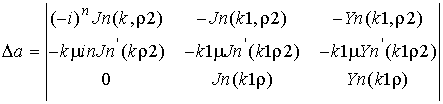– для рассеянной волны.

,

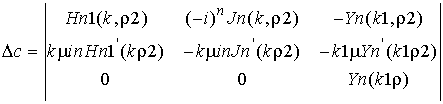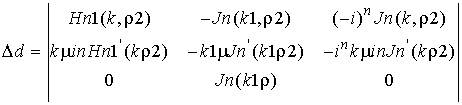- для волны в слое.

В формулах использованы обозначения: k, k1 – волновые векторы в воздухе и оболочке цилиндра соответственно; Jn,Yn,Hn1 – функции Бесселя первого и второго рода, а также функции Ханкеля; ρ, ρ2 – радиус металлического цилиндра и радиус всей структуры с оболочкой; μ,μin – магнитные проницаемости в воздухе и оболочке цилиндра соответственно.

При вычислении неизвестных коэффициентов следует учитывать отрицательный знак волнового вектора, относительной магнитной и электрической проницаемости слоя (т.к. у среды отрицателен показатель преломления). Рассеянная волна описывалась функцией Ханкеля первого рода, чтобы учесть затухание интенсивности поля на бесконечном удалении от цилиндра.

На рис. 2 приведены результаты расчета пространственного распределения амплитуды электрического поля для двух случаев: рассеяние волны на металлическом цилиндре с диэлектрической оболочкой (рис. 2а) и рассеяние волны на металлическом цилиндре оболочкой из метаматериала (рис. 2б).

а		б

Рисунок 2 – Пространственное распределение амплитуды электрического поля для цилиндра а) с диэлектрической оболочкой, б) с оболочкой из метаматериала.

Как видно из рисунков, для случая с метаматериалом происходит фокусировка поля внутри слоя и наблюдается увеличение интенсивности поля возле границы раздела воздух-метаматериал. Обычная диэлектрическая оболочка искажает распределение поля, однако не фокусирует его. Кроме того, результаты расчетов показывают, что параметры и размеры оболочки оказывают довольно сильное влияние на характеристики рассеянного поля за цилиндром. На рис. 3 представлены результаты расчетов радиальных зависимостей интенсивности электрического поля в рассматриваемой системе. Вертикальными штриховыми линиями показаны границы слоя, нанесенного на металлический цилиндр. Рис. 3а соответствует диэлектрическому слою, рис. 3б — слою из метаматериала. Очевидно, что изменение знака показателя преломления среды существенно влияет на закономерности распределения поля. В случае обычного диэлектрического покрытия интенсивность поля спадает практически экспоненциально. Если металлический цилиндр покрыт слоем метаматериала, то зависимость становится немонотонной. В частности, наблюдается локальный минимум интенсивности за пределами структуры.

Для диэлектрика Для метаматериала:

х,м

х,м

I

I

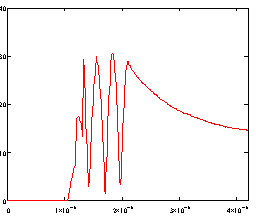
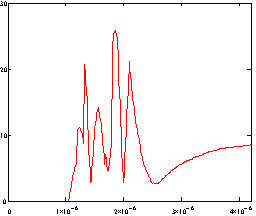
Рисунок 3 – Пространственное распределение интенсивности электрического поля

Графики были построены для отношения диаметра цилиндра к толщине слоя ≈2.

Литература:

1. Li C., Shen Z. Electromagnetic scattering by aconducting cylinder coated with metamaterials // Progress in electromagnetics research. – 2003. – Р. 91-105.

2. Wu Q., Zhang K., Meng F.-Y., Li L.-W. Electromagneting characteristics of metamaterial cloak covered dielectric cylinder illuminated by electric line source // IET Microwaves, Antennas&Propagation. – 2010. – V. 4, Iss.10, P. 1680-1688.