СОЗДАНИЕ РЕШАЮЩЕЙ ФУНКЦИИ ПРИ РАСПОЗНАВАНИИ ОБРАЗОВ В ЭКГ

Кошеков К.Т. Мулдабаев Е.С. Савостин А.А. Саржанов Н.Н.

Северо-Казахстанский государственный университет им. М. Козыбаева Республика Казахстан г. Петропавловск

Конечной целью автоматизированного анализа ЭКС является классификация данного сигнала с целью отнесения его к одной из нескольких известных категорий и получение предварительного диагностического решения, относящегося к состоянию ССС. Необходимо помнить, что ЭКС являются лишь одним из источников информации для постановки диагноза: классификация данного сигнала может оказать существенную помощь в диагностике, но почти ни когда не является единственным фактором.

Создание автоматизированных систем распознавания ЭКС стало возможным после накопления большого объема клинической информации, эмпирически показывающей связь отдельных элементов ЭКГ с физиологическими процессами в миокарде [1]. В результате этого, в процессе анализа сигнала происходит выявление заданных (в зависимости от характера проводимого исследования) количественных признаков, на основании которых ЭКС рассматривается в виде вектора параметров x = (x₁, x₂, …, x_n)^T. Так как элементы x_i являются вещественными числами, то вектор x можно рассматривать как точку в n-мерном пространстве. Поэтому векторы объектов со сходными параметрами будут формировать кластеры. Для примера на рисунке 1 показаны двумерные векторы признаков С1 и С2, z1 и z2 – прототипы этих двух классов, d(x) – оптимальная линейная решающая функция, представляющая собой перпендикуляр, проведенный через середину прямой линии, соединяющей прототипы данных двух классов.

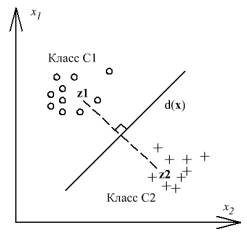
Рисунок 1 – Разделение двумерных векторов признаков на два класса

Для решения задачи классификации образов необходимо создание решающих процедур, для отнесения данных к различным классам образов, основанных на векторах признаков.

Результатом идентификации элементов ЭКС является формирование комплекса диагностических признаков, представленных в компактной форме для удобства их обработки на компьютере.

Например, в работе [2] предлагается следующая интерпретация признаков для зубца P:

- Ширина интерпретируется как длительность P, обозначается ΔP и измеряется в секундах (с);

- Амплитуда обозначается A_P и измеряется в мВ в точке maxP и minP;

- М-образность интерпретируется следующей последовательностью: A_P > 0 и n_A = 3, где n_A – количество экстремумов P;

- Двухфазность P записывается следующим образом: n_A = 2, A_P1 > 0 и A_P2 < 0;

- Остроконечность P с превышением амплитуды можно интерпретировать как P" > P"_max, A_P > 0,25, где P" – вторая производная от зубца P по времени;

- Инвертирование P записывается следующим образом: A_P < 0 для I, II и A_P > 0 в отведении aVR;

- Чередование зубца P и комплекса QRS можно представить как Δ_PR > 0 (для нормальной последовательности – P-R) и Δ_PR < 0 (для обратной последовательности – R-P);

- Отсутствие P интерпретируется, очевидно, как A_P = 0;

- Условие n_P < n_QRS на ΔT > 10(R-R) обозначает: количество зубцов Р меньше, чем количество комплексов QRS на интервале времени большем чем десять интервалов R-R;

- Условие n_P > n_QRS на ΔT > 10(R-R) обозначает: количество зубцов Р больше, чем количество комплексов QRS на интервале времени большем чем десять интервалов R-R;

Таким образом, для описания всех параметров зубца P, регистрируемого в различных отведениях, необходимо составить матрицу p = (p_ij), где - количество признаков, а - количество отведений. Т.е.

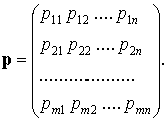(1.1)

Если задан некоторый классифицированный набор векторов признаков, то его можно использовать в роли обучающей выборки [3, 4]. На основании обучающей выборки возможно разработать математические функции, которые будут определять разделение между классами. При помощи этих функций далее осуществляется распознавание новых векторов признаков с неопределенной классификацией. Набор векторов признаков с известной классификацией, используемый для оценки разработанного подобным способом классификатора, называется контрольной выборкой.

Рассмотрим метод создания решающей функции для распознавания линейно разделимых образов в сигнале ЭКС на примере зубца P в одном отведении.

Обобщённая линейная решающая функция задаётся в форме

d(p) = a₁p₁ + a₂p₂ + … + a_np_n + a_n+1 = a^Tp, (1.2)

где p = (p₁, p₂, …, p_n, 1)^T – вектор признаков зубца Р, дополненный добавочным членом, равным единице; a = (a₁, a₂, …, a_n, a_n+1)^T – соответственно, дополненный весовой вектор [5].

При классификации на М классов для принятия решения необходимо наличие М весовых векторов и М решающих функций:

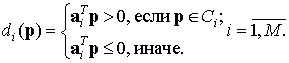(1.3)

В (1.3) a_i = (a_i1, a_i2, …, a_in, a_i,n+1)^T – это весовой вектор для класса С_i.

Если определить для М классов образов их прототипы z₁, z₂, …, z_M как среднее для всех векторов признаков, то евклидово расстояние между произвольным вектором p и i-м прототипом будет иметь вид:

(1.4)

Тогда можно сформулировать правило для классификации вектора p в следующей форме:

(1.5)

Проведем следующие преобразования

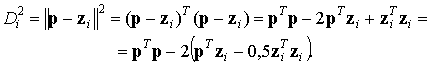(1.6)

Максимум выражения соответствует минимуму значения D²_i, а последнее, в свою очередь, минимуму D_i, так как D_i > 0.

Следовательно, решающая функция будет определена следующим образом:

(1.7)

Тогда решающее правило может быть сформировано в виде:

(1.8)

Еще один способ определения решающего правила основан на утверждении о том, что вектор p должен быть отнесен к тому классу, который является ближайшим к данному вектору признаков. Т.е. если задана выборка из N образцов {s₁, s₂, …, s_N}, и каждый образец принадлежит к одному из М классов {C₁, C₂, …, C_M}, то справедливо выражение:

(1.9)

При данном подходе более надежно определять классификацию на нескольких образцах, т.е. рассматривать некоторое число r ближайших к классифицируемому образцу соседей. Это исключит возможность вынесения итогового решения по пограничным образцам [5, 6].

Список литературы:

1 Микрокомпьютеры в физиологии: Пер с англ./Под ред. П. Фрейзера. – М.; Мир, 1990. – 383 с.

2 Ивель В. П. Автоматизированные системы измерения и анализа электрокардиологических сигналов: Монография/ В. П. Ивель, Г. М. Мутанов. - Алматы: НИЦ "Ғылым", 2002. - 241 c.

3 Загоруйко Н.Г. Методы распознавания и их применение. – М.: «Советское радио», 1972, – 208 с.

4 Горелик А.Л. и др. Современное состояние проблемы распознавания/ А.Л. Горелик, И.Б. Гуревич, В.А. Скрипкин. – М.: Радио и связь, 1985. – 160 с.

5 Ту Дж., Гонсалес Р. Принципы распознавания образов/ Пер. с англ. – М.: Мир, 1978. – 411 с.

6 Дуда Р., Харт П. Распознавание образов и анализ сцен/ Пер. с англ. – М.: Мир, 1976. – 511 с.