УДК: 347.763:621.43:697.328(045)

Абдрахманов А.Б., Оразалиев Б.Т.,Сансызбаева А.А., Тынысбекова С.С.

Теоретические основы теплового расчета аккумуляторов тепла

Аккумуляторы тепла (АТ) находят все более широкое применение в хозяйствах как источник сохранения тепловой энергии и как экологически чистые установки.

Эффективность работы АТ во многом зависит от типа теплоизоляционных материалов и от выбора их толщины в зависимости от температуры среды использования.

Обычного бытового термоса можно представит как АТ выполненных из нержавейки объемом 3-8 литров в зависимости от модели двигателя, для которого он предназначен. Эти сосуды довольно неплохо сохраняют тепло рабочей жидкости непосредственно от системы охлаждения.

Данный вид аккумуляторов тепла в отличие от других капсульных тепловых аккумуляторов имеет меньше габариты, проще в изготовлении, хотя меньше накапливает тепла, но она достаточное для осуществления первого легкого запуска ДВС автомобилей и тракторов в холодное время года [1]. При проектировании аккумуляторов тепла ставится задача не только обеспечение сохранение тепла, а также и обеспечение при этом допускаемых разности температур.

Цилиндры современных двигателей выполняются в виде блока, заодно с верхней частью картера. Такая конструкция называется блок-картером. Обеспечение высокой прочности и жесткости блок-картера – одно из важнейших требований, предъявляемых к конструкции ДВС.

Расчет блок-картера на прочность представляет большие трудности из-за сложности его конфигурации и определения действующих нагрузок. Как правило, расчетным методом находят только напряжения в стенках цилиндра.

Допускаемые напряжения растяжения для чугунных гильз цилиндров принимается 40…60 МПа, а для стальных принимается 80…120 МПа.

При работе двигателя между внутренней и наружной поверхностями гильзы цилиндров возникает значительный перепад температур, вызывающий тепловые напряжения [4]:

_t = E _ц ∆t / [2 (1-µ)], (1)

где Е – модуль упругости материала гильзы;

_ц - коэффициент его линейного расширения;

∆t – перепад температур, °С (на основании опытных данных, ∆t = 100…150°С);

µ - коэффициент Пуассона.

Суммарные напряжения от давления газов и перепада температур на наружной и внутренней поверхностях гильзы цилиндров

= ; = ;

Суммарное напряжение в чугунной гильзе не должно превышать 100…130 МПа, стальной - 180…200 МПа.

Предположим, рассматриваемый аккумулятор тепла представляет форму цилиндрического сосуда, тогда через цилиндрическую однородную стенку переносится тепло при стационарном режиме от горячей среды с постоянной температурой t₁ и коэффициентом теплоотдачи ₁, к холодной среде с постоянной температурой t₂ и коэффициентом теплоотдачи ₂ (рис.1). Теплопередача при этом представляет собой весьма сложный процесс, в котором тепло передается всеми тремя способами: теплопроводностью, конвекцией и излучением. Количество теплоты, передаваемой горячей средой к внутренней стенке цилиндра путем конвективного теплообмена, определяется по

уравнению Ньютона – Рихмана [3]:

, (2)

где a₁ - коэффициент теплоотдачи от горячей среды с постоянной температурой t₁ к внутренней поверхности стенки, учитывающий все виды теплообмена;

- расчетная внутренняя поверхность стенки, м².

Тепловой поток, передаваемой теплопроводностью через цилиндрическую стенку, определяется по уравнению

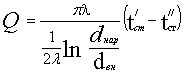. (3)

Тепловой поток, передаваемой от наружной стенки к холодной среде, определяется по той же формуле конвективного теплообмена Ньютона – Рихмана:

, (4)

где a₂ - коэффициент теплоотдачи от второй наружной поверхности стенки к холодной среде с постоянной температурой t₂;

- расчетная наружная поверхность стенки, м².

Величины Q в уравнениях (2),(3) и (4) одинаковы.

Решая эти три уравнения относительно разности температур, а затем, складывая их почленно, получим

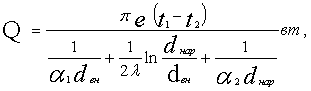
(5)

где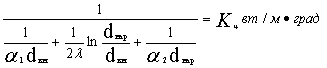

называют линейным коэффициентом теплопередачи.

Плотность теплового потока, проходящего через цилиндрическую стенку, будет

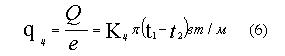
Числовое значение линейного коэффициента теплопередачи цилиндрической стенки К_ц есть количество теплоты, проходящей через один метр цилиндрической формы сосуда в единицу времени от горячей к холодной среде при разности температур между ними в 1 градус.

А результирующий поток теплоты при этом всегда направлен в сторону уменьшения температуры.

Уравнение (5) также можно написать в следующем виде:

Q=K (t-t)вт (7)

При рассматривать перенос теплоты через многослойную цилиндрическую стенку, имеющую n слоев, тепловой поток будет равен

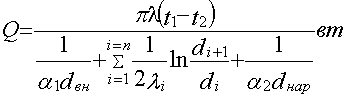(8)

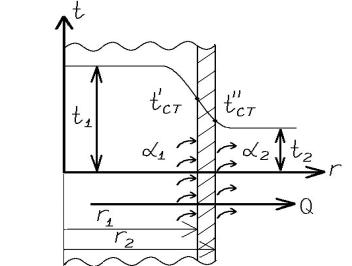
Рис.1. Распределение температуры в плоской цилиндрической стенке

Плотность теплового потока, отнесенная к внутренней или наружной поверхности, определяется по уравнениям

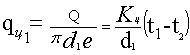вт/м^2; (9)

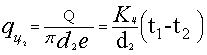вт/м.² (10)

Величину, обратную коэффициенту теплопередачи, 1/К_ц называют полным линейным термическим сопротивлением теплопередачи через цилиндрическую стенку:

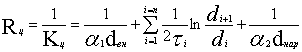,м•град/вт, (11)

где и - термические сопротивления теплоотдачи;

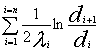- термическое сопротивление многослойной цилиндрической стенки.

Температуру внутренней поверхности определяем по формуле

⁰С, (12)

а температуру наружной поверхности

⁰С . (13)

Так как теплоотдача является достаточно сложным процессом и коэффициент теплоотдачи a зависит от многих факторов, но при решении инженерных задач его принимают в большинстве случаев величиной постоянной [5].

Всякое покрытие горячей поверхности называют тепловой изоляцией, которое способствует снижению потерь теплоты в окружающую среду.

Для тепловой изоляции могут быть использованы любые материалы с низким коэффициентом теплопроводности – асбест, пробка, слюда, шлаковая, минеральная или стеклянная вата, шерсть и др.

Анализ формулы полного линейного термического сопротивления теплопередачи цилиндрической стенки показывает, что тепловые потери изолированных цилиндров уменьшаются не пропорционально увеличению толщины изоляции.

Теперь рассмотрим условие, при котором материал, используемый для изоляции цилиндра, будет уменьшать тепловые потери.

Пусть цилиндр покрыта однослойной изоляцией.

Приняв постоянными ,,,,,, и рассмотрим, как будет изменяться полное термическое сопротивление при изменении толщины изоляции.

В уравнении полного термического сопротивления двухслойной цилиндрической стенки при увеличении внешнего диаметра изоляции

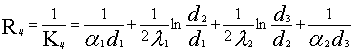(14)

увеличивается сопротивление слоя изоляции (член 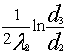), но

одновременно уменьшается сопротивление теплоотдачи на наружной поверхности изоляции (член ).

Взяв первую производную от правой части уравнения (14) по и приравнивая ее нулю, получаем

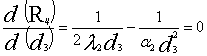. (15)

Тогда критический диаметр изоляции, отвечающий экстремальной точке кривой R= f (), определится формулой

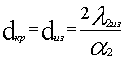. (16)

Из уравнения (15) следует, что критический диаметр изоляции не зависит от размеров цилиндра.

Он будет тем меньше, чем меньше коэффициент теплопроводности изоляции и чем больше коэффициент теплоотдачи ₂ от наружной поверхности изоляции к окружающей среде.

Вторая производная от R_ц больше нуля. Следовательно, критический диаметр соответствует минимуму теплового сопротивления и максимуму теплового потока (рис.2). Анализ уравнения (16) показывает, что если наружный диаметр изоляции d_из увеличивается, но остается меньше d_кр, то тепловые потери возрастают и будут больше теплопотерь голого цилиндра (кривая АК).

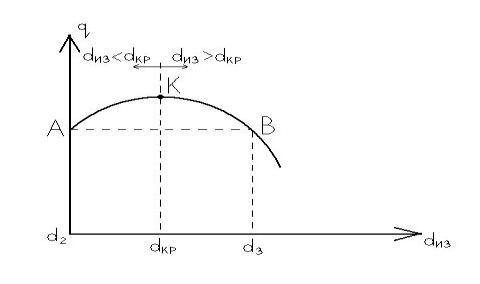
Рис.2. Зависимость изменения теплового потока от наружного диаметра изоляции

При равенстве получаются максимальные теплопотери в окружающую среду (точка К). При дальнейшем увеличении наружного диаметра изоляции теплопотери будут меньше, чем при

(кривая ВК).

Только при тепловые потери вновь станут такими же, как и для неизолированного цилиндра.

Значить, для эффективной работы изоляции необходимо, чтобы критический диаметр был меньше внешнего диаметра оголенного цилиндра, чтобы (см. рис.2).

Таким образом, для того чтобы изоляция вызвала уменьшение теплопотерь цилиндрической стенки по сравнению с голым цилиндром при данном наружном диаметре цилиндра d₂ и заданном коэффициенте теплоотдачи ₂, необходимо

(17)

Например, для изоляции цилиндра диаметром 300мм имеется шлаковая вата с коэффициентом теплопроводности _из = 0,1 вт/м•град; коэффициент теплоотдачи ₂ = 4,0 вт/м² •град.

Целесообразно ли применять в данном случае в качестве изоляции шлаковую вату?

Критический диаметр изоляции

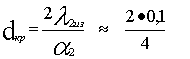= 0,05м = 50мм.

Так как , шлаковую вату в рассматриваемом случае применять можно.

Для нашей задачи _из должен быть меньше:

вт/м•град.

Выводы:

Подводя итоги теплового расчета выборов изоляционных материалов для аккумуляторов тепла можно констатировать, что:

· Позволяет экономить изоляционных материалов;

· Оптимизировать толщины материалов в зависимости от температуры среды использования;

· Снизить износа ДВС;

· Снизить расходов эксплуатационных материалов и времени на первый запуск ДВС в холодное время года.

Литература

1. Бекман Г, Гилли П. Тепловое аккумулирование энергии: Пер. с англ. – М.:Мир, 1987. – 272 с.

2. Виноградов В. С. Техническая термодинамика и теплопередача в примерах и задачах. Учебное пособие. Комсомольск-на-Амуре, 2012.

3. Железко Б. Е., Адамов В. М. Есьман Р. И. Техническая термодинамика, теплопередача и двигатели внутреннего сгорания. – Мн.: Выш. шк.,1985.-271с.

4. Николаенко А.В. Теория, конструкция и расчет автотракторных двигателей. М.: Колос,1984.-335с.

5. Теплотехника. //Под. ред. В. Н. Луканина. – М,: Высшая школа, 2002.