к.т.н. Новиков А.Н., Новикова Е.Е.

Военная академия РВСН имени Петра Великого

ОПТИМАЛЬНАЯ ЦИФРОВАЯ ОБРАБОТКА ШИРОКОПОЛОСНЫХ СИГНАЛОВ В АНТЕННАХ СОТОВОЙ СВЯЗИ

В современных радиоэлектронных системах (РЭС) все большее применение находят широкополосные сигналы, которые позволяют повысить скорость передачи информации. Однако плотное размещение радиоэлектронных систем различного назначения зачастую сводит на нет их возможности из-за нарушения условий электромагнитной совместимости. Для РЭС, использующих узкополосные сигналы, хорошо разработаны методы подавления нежелательных излучений путем формирования «нулей» диаграммы направленности (ДН) в требуемых направлениях [1-3]. Следует отметить, что существующие методы в случае пространственной обработки узкополосных сигналов легко реализуются с использованием цифровых диаграммообразующих схем (ЦДС) [4]. Однако для широкополосных сигналов существующие методы пространственной обработки неприменимы.

Цель доклада – разработка алгоритма определение оптимальной частотной зависимости весовых коэффициентов в ЦДС и исследование закономерностей формирования диаграмм направленности адаптивных антенных решеток (ААР) с ЦДС при пространственной обработке широкополосных сигналов.

Рассмотрим -элементную ААР с ЦДС с известной геометрией излучающего раскрыва, обеспечивающую прием полезного сигнала в присутствии широкополосных помех. Направление прихода и спектр полезного сигнала () являются известными, аналогичные параметры помеховых сигналов ‑ неизвестными. Требуется определить частотные зависимости весовых коэффициентов в каналах ААР, обеспечивающих в заданной полосе частот оптимальное подавление помеховых сигналов в соответствии с критерием максимума отношения сигнал/(помеха+шум) (ОСПШ).

На основе формулировки критерия оптимальной обработки узкополосного сигнала по максимуму ОСПШ [1] сформулируем аналогичный критерий для широкополосного сигнала в следующем виде:

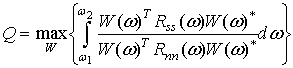, (1)

где – частотно-зависимая ковариационная матрица полезного сигнала; – частотно-зависимая ковариационная матрица сигналов помех; ‑ частотно-зависимый вектор весовых коэффициентов; , – определяют полосу частот, в которой обрабатывается полезный сигнал; , – символы операций транспонирования и комплексного сопряжения соответственно.

Интеграл (1) принимает максимальное значение, в том и только и том случае, когда подынтегральное выражение является максимальным для каждой частоты. Это позволяет на основе решения задачи оптимизации для узкополосных сигналов [1-3] представить оптимальную частотную зависимость весовых коэффициентов в виде:

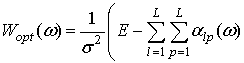
, (2)

где – вектор-столбец, элементы которого определяют формирование ДН заданной формы в отсутствии помех; , () ‑ вектор-столбец, элементами которого являются комплексные амплитуды -го помехового на выходе излучателей ААР; ‑ единичная матрица; ‑ мощность тепловых шумов; ‑ частотно-зависимый коэффициент, определяемый из свойств ковариационной матрицы помех.

Из соотношения (2) можно сделать вывод, что на частотах, где при оптимальной пространственной обработке формирование «нуля» ДН не должно происходить.

Исследование возникающих закономерностей проведем на примере антенной решетки с круговым раскрывом из излучателей. Излучатели расположены в узлах гексагональной сетки с шагом ( ‑ длина волны, соответствующая средней частоте диапазона полезного сигнала). При моделировании рассматривался прием полезного сигнала, представляющего собой 13-позиционную посылку на основе кода Баркера, приходящего с направления в присутствии одного помехового сигнала. Полоса частот спектра полезного сигнала имеет границы , . Модель помехового сигнала определяется направлением прихода и спектром вида:

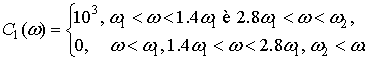
Соответствующие данным сигнально-помеховым ситуациям диаграммы направленности ААР приведены на рис.1-3 (кривая 1 – в отсутствии помехи, 2 ‑ при наличии помехи). Во всех случаях на рисунках с индексом «а» показаны ДН на частоте , на рисунках с индексом «б» – ДН на центральной частоте и на рисунках с индексом «в» – ДН на частоте .

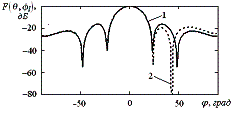
а)

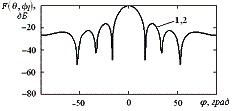
б)

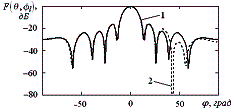
в)

Рис.1. ДН ААР для третьего случая сигнально-помеховой ситуации

Проведенное моделирование показывает (рис.1), что для заданного случая сигнально-помеховой ситуации формирование «нулей» ДН происходит только в полосах частот и . Таким образом, результаты моделирования подтверждают, что при оптимальной пространственной обработке широкополосных сигналов формирование «нулей» ДН происходит только на тех частотах, где спектральная плотность помехи не равна нулю.

Литература

1. Монзинго Р.А., Миллер Т.У. Адаптивные антенные решётки. – М.: Радио и связь, 1986, 448с.

2. Пистолькорс А.А., Литвинов О.С. Введение в теорию адаптивных антенн. – М.: Наука, 1991, 200с.

3. Журавлёв А.К., Лукошин А.П., Поддубный С.С. Обработка сигналов в адаптивных антенных решётках. – Л: Изд-во ЛГУ, 1983.

4. Слюсарь В.И. Smart-антенны пошли в серию. – Электроника: НТБ, 2004, № 2, с. 62-65.