Д.т.н. Сулейменов О.А.

Таразский государственный университет, Казахстан

ПРОЦЕСС ЗАРЯДКИ ЧАСТИЦ В ПОЛЕ КОРОННОГО

РАЗРЯДА пульсирующего напряжения и ПЕРИОДИЧЕСКИХ БИПОЛЯРНЫХ ИМПУЛЬСОВ

При исследовании индукционной зарядки частиц задача представлена в следующем виде: на заряженную проводящую плоскость, создающую однородное поле, помещается незаряженное тело, имеющее форму половины трехосного эллипсоида, причем большая полуось расположена перпендикулярно к проводящей плоскости /I/. Диэлектрическая проницаемость тела ε₁ и среды ε₂, объемная проводимость тела γ₁ и среды γ₂ заданы.

Постоянная времени переходного процесса, согласно / I,2 /, запишется в следующем виде:

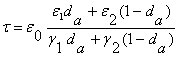( 1 )

где d_a - коэффициент деполяризации.

Частицы полуэллипсоидальной формы с полуосями b и с, объемной проводимостью γ₁ и относительной диэлектрической проницаемостью ε₁, находящиеся на заземленном осадительном электроде в поле ионизированного воздуха (γ₂, ε₂) приобретают предельный заряд 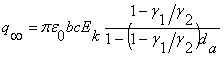/2/.

(2)

где Е_к – напряженность объемного заряда.

Следует отметить, что в случаях γ₁>γ₂ частицы, имеющие контакт с осадительным электродом в поле коронного разряда, приобретают индукционный заряд, а постоянная времени зарядки определяется из формулы (1). В случаях γ₁ » γ₂, что соответствует хорошему проводнику, удельная объемная проводимость среды практически не влияет на значение τ_з, в этом можно убедиться подставив в формулу (1) значения параметров d_a и γ₂ обычных условий (ε₀ = 8,85×10^-12 Ф×м^-1).

Учитывая, что при наличии напряжения подпора во время паузы на частицу, находящуюся на осадительном электроде, воздействует кулоновское поле, наводящее на нее индукционный заряд предельного значения q_un, аналогично случаю при импульсном напряжении, запишем уравнение кинетики зарядки в зависимости от количества пульсации.

Пульсирующий режим высоковольтного питания с высоким значением напряжения подпора не обеспечит повышенную напряженность поля из-за близости напряжения подпора критическому напряжению. Предположим, что в режиме близком к установившемуся, зарядка происходит за время пульсации, а за время паузы происходит разрядка частицы.

На основе уравнений, полученных в импульсном и пульсирующих режимах высоковольтного питания, для установившегося режима можно записать

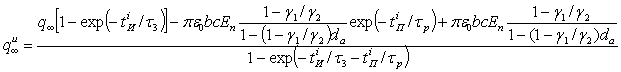
(3)

В самых благоприятных условиях ограничения заряда частиц полупроводников, после каждого периода остаточное значение заряда не может быть меньше

1- g₁/g₂

q_un = pe₀bcE_n ¾¾¾¾¾¾ exp(-tⁱ_и /t₃) (4)

1-(1- g₁/g₂)d_a

Следовательно, в рассматриваемом режиме, для полупроводников с удельной объемной проводимостью менее 0,25×10^-9Ом^-1×м^-1, избежать их избыточной зарядки в поле пульсирующего коронного разряда не удается.

Рассмотрим случай, когда импульсы одной полярности образуют коронный разряд, а импульсы другой полярности имеют амплитуду ниже напряжения возникновения коронного разряда. Накопленный заряд частицы, имеющей удельную объемную проводимость менее 0,25×10^-9Ом^-1×м^-1, в зависимости от количества импульсов равен

q [1-exp(-tⁱ_и / t₃₎]exp(-tⁱ_п /t_p)-pe₀bcd_a^-1E _n exp(-tⁱ_п /t_p)+ pe₀bcd_a^-1E _n

q^u_¥[nT] = ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾

1-exp(-tⁱ_и /t₃- tⁱ_п /t_p)

×{1-exp[-n(tⁱ_и / t₃ + tⁱ_п /t_p)]} (5)

Предельный заряд в режиме насыщения

q [1-exp(-tⁱ_и / t₃)]exp(-tⁱ_п /t_p) - pe₀bcd_a^-1E _n exp(-tⁱ_п /t_p) + pe₀bcd_a^-1E _n

q^u_¥= ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾ (6)

1-exp(-tⁱ_и /t₃- tⁱ_п /t_p)

Расчетное значение заряда, индуцируемого напряжением подпора (импульсом малой амплитуды), указывает на одинаковую полярность зарядов, сообщаемых при ударной и индукционной зарядке. Нижний предел избыточного заряда, сообщаемого ионизацией, задается значением напряжения подпора, которая не допускает полную разрядку полупроводниковых частиц на осадительном электроде.

Литература

1. Джуварлы Ч.М., Вечхайэер Г.В., Штейншрайбер, В.Я. Трехосный диэлектрический элипсоид в электрическом поле при учете проводимости. - Изв. АН СССР, Энергетика и транспорт, 1969, №- I, с. 158-162.

2. И.П. Верещагин, В.И. Левитов, Г.З. Мирзабекян, М.М. Пашин. Основы электрогазодинамики дисперсных систем. М., Энергия, 1974,с. 480.