УДК 517.443
М.П.Ленюк, Г.Я.Стопень
ОБЧИСЛЕННЯ НЕВЛАСНИХ ІНТЕГРАЛІВ ЗА ВЛАСНИМИ ЕЛЕМЕНТАМИ
ГІБРИДНОГО ДИФЕРЕНЦІАЛЬНОГО ОПЕРАТОРА БЕССЕЛЯ-ФУР’Є-ЕЙЛЕРА НА ПОЛЯРНІЙ ВІСІ r
³ R0 > 0
Розглянемо задачу про конструкцію обмеженого
на множині ![]() = {r: r
Î (R0, R1)
= {r: r
Î (R0, R1) ![]() (R1, R2)
(R1, R2) ![]() (R2, ¥), R0 > 0} розв’язку сепаратної системи диференціальних рівнянь Бесселя,
Фур’є та Ейлера
(R2, ¥), R0 > 0} розв’язку сепаратної системи диференціальних рівнянь Бесселя,
Фур’є та Ейлера
![]() , r Î (R0, R1),
, r Î (R0, R1),
![]() , r Î (R1, R2), (1)
, r Î (R1, R2), (1)
![]() , r Î (R2, ¥R3)
, r Î (R2, ¥R3)
за крайовими умовами
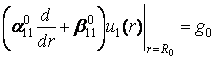 ,
, ![]() (2)
(2)
та умовами спряження
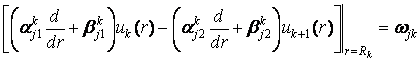 , j, k = 1, 2. (3)
, j, k = 1, 2. (3)
У системі (1) беруть участь диференціальні оператори Бесселя
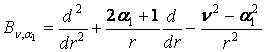 [1] Ейлера
[1] Ейлера 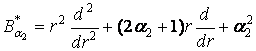 [2], 2aj
+ 1 > 0 , n ³ a1 ³ 1/2, та Фур’є
d2/dr2.
[2], 2aj
+ 1 > 0 , n ³ a1 ³ 1/2, та Фур’є
d2/dr2.
Припустимо, що виконані
умови на коефіцієнти: qj > 0, ![]() £ 0,
£ 0, ![]() ³ 0, |
³ 0, |![]() | +
| + ![]() ¹ 0,
¹ 0, ![]() ³ 0,
³ 0, ![]() ³ 0, c1k c2k > 0, cjk =
³ 0, c1k c2k > 0, cjk = ![]() , j, k = 1, 2.
, j, k = 1, 2.
Фундаментальну систему розв’язків для
диференціального рівняння Бесселя (![]() )v =
0 утворюють модифіковані функції Бесселя першого роду
)v =
0 утворюють модифіковані функції Бесселя першого роду ![]() (q1r) та другого роду
(q1r) та другого роду ![]() (q1r) [1] ; фундаментальну систему розв’язків для
диференціального рівняння Фур’є (d2/dr2 –
(q1r) [1] ; фундаментальну систему розв’язків для
диференціального рівняння Фур’є (d2/dr2 – ![]() )v = 0 утворюють функції v1 = chq2r та v2 = shq2r [2]; фундаментальну систему розв’язків для
диференціального рівняння Ейлера (
)v = 0 утворюють функції v1 = chq2r та v2 = shq2r [2]; фундаментальну систему розв’язків для
диференціального рівняння Ейлера (![]() )v =
0 утворюють функції v1 =
)v =
0 утворюють функції v1 = ![]() та v2 =
та v2 = ![]() [2].
[2].
Наявність
фундаментальної системи розв’язків дозволяє будувати загальний розв’язок
крайової задачі (1) – (3) методом функцій Коші [2, 3]:
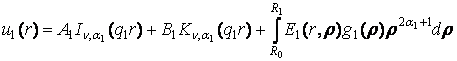 ,
,
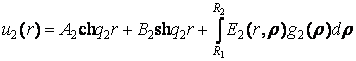 , (4)
, (4)
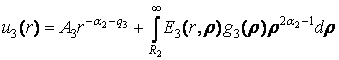 .
.
Тут Ej(r, r) – функції Коші [2, 3]:
![]()
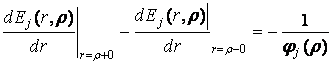 , (5)
, (5)
j1(r) = ![]() , j2(r) = 1, j3(r) =
, j2(r) = 1, j3(r) = ![]() .
.
Введемо до розгляду функції:
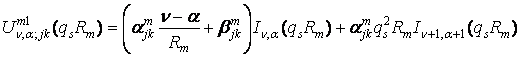 ,
,
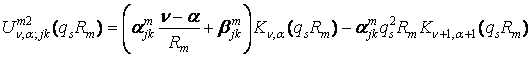 ,
,
![]() , j = 1, 2,
, j = 1, 2,
![]() .
.
Безпосередньо перевіряється, що функція Коші
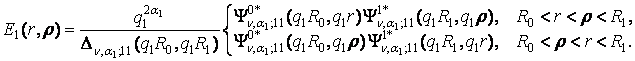 (6)
(6)
Визначимо функції
![]() ,
, ![]() ,
,
![]() , j, k =1, 2,
, j, k =1, 2,
![]() .
.
Безпосередньо
перевіряється, що функція Коші
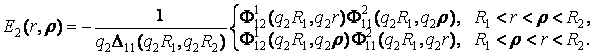 (7)
(7)
Припустимо, що функція Коші

Властивості
(5) функції Коші дають алгебраїчну систему з двох рівнянь:
![]() ,
,
![]() .
.
Звідси отримуємо співвідношення:
![]() , D1 =
, D1 = ![]() . (8)
. (8)
Доповнимо систему (8) алгебраїчним рівнянням:
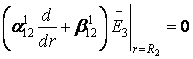 :
: ![]() . (9)
. (9)
Із алгебраїчної системи (8), (9) знаходимо, що
![]() .
.
Цим
функція Коші E3(r, r) визначена й внаслідок симетрії відносно
діагоналі r = r має структуру:
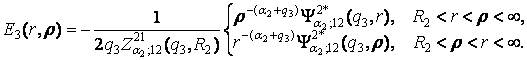 (10)
(10)
У рівностях (9), (10) беруть участь функції:
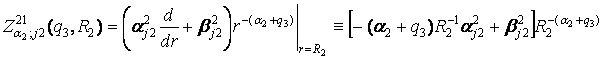 ,
,
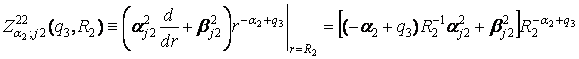 ,
,
![]() , j = 1, 2.
, j = 1, 2.
Повернемося до формул (4). Крайова умова в
точці r = R0 та умови спряження (3) для визначення величин Aj (j = ![]() ) та Bk (k = 1, 2) дають неоднорідну алгебраїчну систему
з п’яти рівнянь:
) та Bk (k = 1, 2) дають неоднорідну алгебраїчну систему
з п’яти рівнянь:
![]() ,
,
![]() ,
,
![]() , (11)
, (11)
![]() ,
,
![]() .
.
В алгебраїчній
системі (11) беруть участь функції:
G12 = 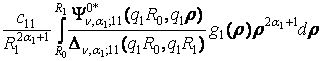 +
+ 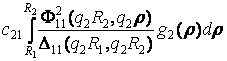 ,
,
G23 = –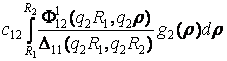 +
+ 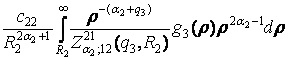 .
.
Визначимо функції:
![]() D2j(q2R1, q2R2)
–
D2j(q2R1, q2R2)
– ![]() D1j(q2R1, q2R2),
D1j(q2R1, q2R2),
![]() =
= ![]() Dj1(q2R1, q2R2) –
Dj1(q2R1, q2R2) – ![]() Dj2(q2R1, q2R2), j = 1, 2.
Dj2(q2R1, q2R2), j = 1, 2.
![]() (r, q) =
(r, q) = ![]() –
– ![]() ,
,
![]() (r, q) =
(r, q) = ![]() –
– ![]() .
.
Припустимо,
що виконана умова однозначної розв’язності крайової задачі (1) – (3): визначник
алгебраїчної системи (11)
Dn, (a)(q) º ![]() =
=
= ![]() (q0R1, q1R1)
(q0R1, q1R1)![]() (q) –
(q) – ![]() (q1R0, q1R1)
(q1R0, q1R1)![]() (q) ¹ 0, (12)
(q) ¹ 0, (12)
(a) = (a1, a2), (q) = (q1, q2, q3).
Введемо до розгляду головні
розв’язки крайової задачі (1) – (3):
1) породжені крайовою умовою в точці r = R0 функції Гріна
Wn, (a); 11(r, q) = 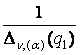 [
[![]() –
– ![]() ], (13)
], (13)
Wn, (a); 12(r, q) = 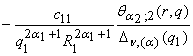 , Wn, (a); 13(r, q) =
, Wn, (a); 13(r, q) = 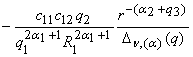 ,
,
2) породжені неоднорідністю умов спряження функції Гріна
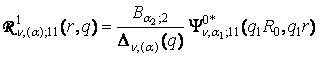 ,
, 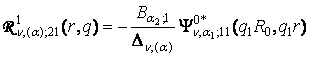 ,
,
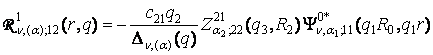 ,
,
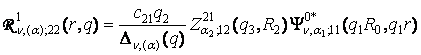 , (14)
, (14)
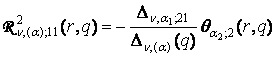 ,
, 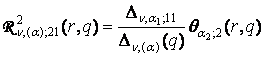 ,
,
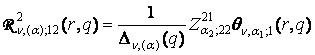 ,
, 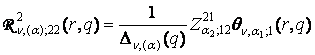 ,
,
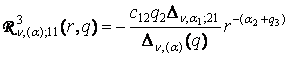 ,
, 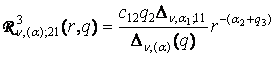
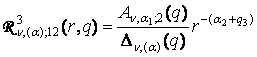 ,
, 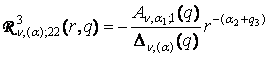 ;
;
3) породжені
неоднорідністю системи (1) функції впливу
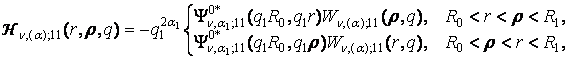
![]()
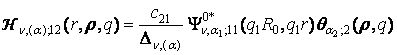 ,
,
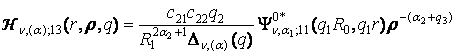 ,
,
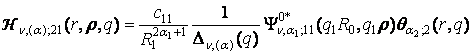 ,
,
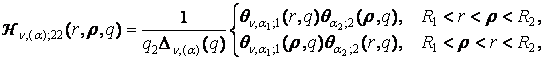 (15)
(15)
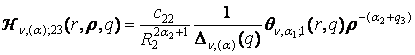 ,
,
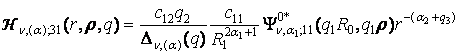 ,
,
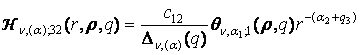 ,
,

У результаті однозначної розв’язності
алгебраїчної системи (11) в силу умови (12), підстановки обчислених значень
величин Aj (j = ![]() ) та Bk (k = 1, 2) у формули (4) маємо єдиний розв’язок
райової задачі (1) – (3):
) та Bk (k = 1, 2) у формули (4) маємо єдиний розв’язок
райової задачі (1) – (3):
uj(r) = Wn, (a); 1j(r, q)g0 + 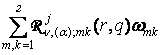 +
+ 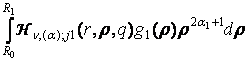 +
+ 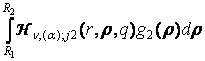 +
+ 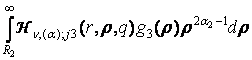 , j =
, j = ![]() . (16)
. (16)
Побудуємо тепер загальний розв’язок крайової
задачі (1) – (3) методом гібридного інтегрального перетворення, породженого на
множині ![]() гібридним
диференціальним оператором (ГДО)
гібридним
диференціальним оператором (ГДО)
![]() +
+ ![]() , (17)
, (17)
де функція q(x) – одинична функція Гевісайда [3].
Оператор Mn, (a) самоспряжений (як
сполучення самоспряжених операторів) і має одну особливу точку r = ¥. Тому його
спектр дійсний та неперервний [4]. Можна вважати, що
спектральний параметр b Î (0, ¥).
Відповідну спектральну функцію Vn, (a)(r, b) = {Vn, (a); 1(r, b); Vn, (a); 2(r, b); Vn, (a); 3(r, b)} знайдемо як розв’язок системи
диференціальних рівнянь
[![]() ]Vn, (a); 1(r, b) = 0, r Î (R0, R1),
]Vn, (a); 1(r, b) = 0, r Î (R0, R1),
[![]() ]Vn, (a); 2(r, b) = 0, r Î (R1,
R2) (18)
]Vn, (a); 2(r, b) = 0, r Î (R1,
R2) (18)
[![]() ]Vn, (a); 3(r, b) = 0, r Î (R2,
¥)
]Vn, (a); 3(r, b) = 0, r Î (R2,
¥)
за крайовими умовами
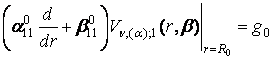 ,
, ![]() (19)
(19)
та умовами спряження
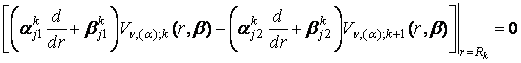 ,
,
j, k = 1, 2. (20)
Тут bj = (b 2 + ![]() )1/2,
)1/2,
![]() ³ 0, j =
³ 0, j = ![]() .
.
Фундаментальну
систему розв’язків для диференціального рівняння Бесселя (![]() )v = 0 утворюють функції Бесселя
)v = 0 утворюють функції Бесселя ![]() (b1r)
та
(b1r)
та ![]() (b1r)
[1]; фундаментальну систему розв’язків для диференціального рівняння Фур’є (
(b1r)
[1]; фундаментальну систему розв’язків для диференціального рівняння Фур’є (![]() )v = 0 утворюють функції v1 = cos b2r та
v2 = sin b2r [2]; фундаментальну систему розв’язків для
диференціального рівняння Ейлера (
)v = 0 утворюють функції v1 = cos b2r та
v2 = sin b2r [2]; фундаментальну систему розв’язків для
диференціального рівняння Ейлера (![]() )v = 0 - функції v1 =
)v = 0 - функції v1 = ![]() та v2 =
та v2 = ![]() [2].
[2].
Наявність фундаментальної системи розв’язків
дозволяє написати рівності
Vn, (a); 1(r, b) = A1![]() (b1, r) + B1
(b1, r) + B1![]() (b1, r),
(b1, r),
Vn, (a); 2(r, b) = A2cos b2r + B2sin
b2r, (21)
Vn, (a); 3(r, b) = A3![]() + B2
+ B2![]() .
.
Крайова умова в
точці r = R0 та
умови спряження (20) для визначення величин Aj та Bj (j = ![]() ) дають алгебраїчну
систему з п’яти рівнянь:
) дають алгебраїчну
систему з п’яти рівнянь:
![]() ,
,
![]() , j = 1, 2;
, j = 1, 2;
![]() . (22)
. (22)
Функції, які беруть участь в системі (22), загальноприйняті [4, 5].
Визначимо функції:
![]() ,
,
![]() , j, k = 1, 2;
, j, k = 1, 2;
![]() , j = 1, 2,
, j = 1, 2,
![]() , j = 1, 2.
, j = 1, 2.
Безпосередньо перевіряється, що в результаті
розв’язання системи (22) та підстановки результату в (21) маємо функції:
Vn,(a);1(r,b)=c21c22b2b3![]() [
[![]() –
– ![]() ],
],
Vn, (a); 2(r, bn) = c22b3[![]() ],
],
Vn, (a); 3(r, bn) = wn, (a); 2(b)![]() cos (b3
ln r) – wn, (a); 1(b)
cos (b3
ln r) – wn, (a); 1(b)![]() sin (b3
ln r).
sin (b3
ln r).
Введемо до розгляду спектральну густину
Wn, (a)(b) = b[b3(b)]–1([wn, (a); 1(b)]2 + [wn, (a); 2(b)]2)–1
та вагову
функцію
s(r) = q(r – R0)q(R1 – r)s 1![]() + q(r – R1)q(R2 – r)s 2 + q(r – R2)s 3
+ q(r – R1)q(R2 – r)s 2 + q(r – R2)s 3![]() ,
,
де s1
= c11c12 ![]() : c21c22
: c21c22![]() , s2 = c12
, s2 = c12![]() : c22, s3 = 1.
: c22, s3 = 1.
Наявність спектральної функції Vn, (a)(r, b), вагової функції s(r) та спектральної густини Wn, (a)(b) дозволяє
визначити пряме Hn, (a) та обернене ![]() гібридне інтегральне
перетворення (ГІП), породжене на множині
гібридне інтегральне
перетворення (ГІП), породжене на множині ![]() ГДО Mn, (a)
за правилами [4]:
ГДО Mn, (a)
за правилами [4]:
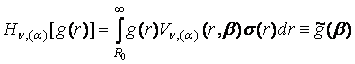 , (23)
, (23)
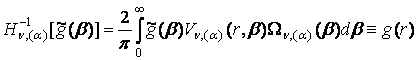 . (24)
. (24)
Тут вектор-функція g(r) належить області визначення ГДО Mn, (a).
Єдиний
розв’язок крайової задачі (1) – (3), побудований за логічною схемою, викладеною
в роботі [5], має структуру:
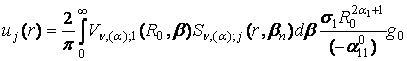 +
+ 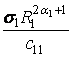 ´
´
´ 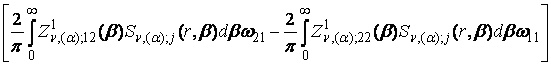 +
+
+ ![]()
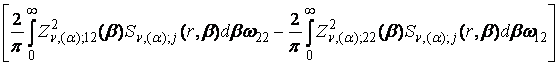 +
+
+ 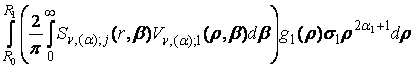 +
+
+ 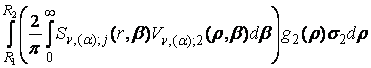 + (25)
+ (25)
+ 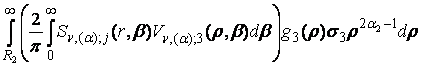 , j =
, j = ![]() .
.
У рівностях (25) беруть участь функції:
![]() =
= ![]() , q2 = max{
, q2 = max{![]() },
},
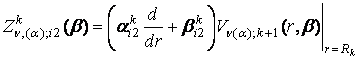 ; i, k = 1, 2; j =
; i, k = 1, 2; j = ![]() .
.
Порівнюючи розв’язки (16) та (25) в силу
єдиності, одержуємо наступні формули обчислення невласних поліпараметричних
інтегралів за власними елементами ГДО Mn, (a):
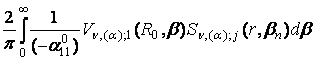 =
= 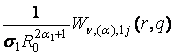 ; j =
; j = ![]() , (26)
, (26)
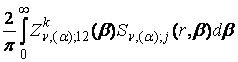 =
= ![]() , k = 1, 2, j =
, k = 1, 2, j = ![]() , (27)
, (27)
 =
= ![]() , k = 1, 2, j =
, k = 1, 2, j = ![]() , (28)
, (28)
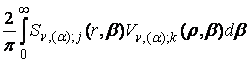 =
= 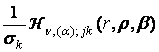 , j, k =
, j, k = ![]() , (29)
, (29)
y 1
= c11 : s1![]() , y 2
= c12 : s2 .
, y 2
= c12 : s2 .
Функції Гріна Wn, (a); 1j(r, q) визначені формулами
(13), функції Гріна ![]() визначенні формулами (14); функції впливу Hn, (a); jk(r, r, q) визначені формулами (15).
визначенні формулами (14); функції впливу Hn, (a); jk(r, r, q) визначені формулами (15).
Підсумком викладеного вище служить твердження.
Теорема. Якщо вектор-функція f(r) = {![]() } неперервна на множин
} неперервна на множин ![]() , а функції gj(r)
задовольняють крайові умови (2) та умови спряження (3) і виконується умова (12)
однозначної розв’язності крайової задачі (1) – (3), то мають місце формули (26)
– (29) обчислення поліпарметричних інтегралів за власними елементами ГДО
, а функції gj(r)
задовольняють крайові умови (2) та умови спряження (3) і виконується умова (12)
однозначної розв’язності крайової задачі (1) – (3), то мають місце формули (26)
– (29) обчислення поліпарметричних інтегралів за власними елементами ГДО ![]() , визначеного рівністю
(17).
, визначеного рівністю
(17).
Література
1.
Ленюк
М.П. Исследование основных краевых задач для диссипативного волнового уравнения
Бесселя. – Киев, 1983. – 62 с. – (Препринт / АН УССР. Ин-т математики; 83.3).
2.
Степанов
В.В. Курс дифференциальных уравнений. – М.: Физматгиз, 1959. – 468 с.
3.
Шилов
Г.Е. Математический анализ. Второй специальный курс. – М.: Наука, 1965. – 328
с.
4.
Ленюк
М.П., Шинкарик М.І. Гібридні інтегральні перетворення (Фур’є, Бесселя,
Лежандра). Частина 1. – Тернопіль: Економічна думка, 2004. – 368 с.
5.
Ленюк
М.П. Обчислення невласних інтегралів методом гібридних інтегральних перетворень
(Фур’є, Бесселя, Лежандра). Том V. –
Чернівці: Прут, 2005. – 368 с.