Карачун В.В., Мельник В.Н.

Национальный технический университет Украины «КПИ»

ВЛИЯНИЕ НЕРЕГУЛЯРНОСТИ ВОЗМУЩАЮЩИХ ФАКТОРОВ НА ПОГРЕШНОСТЬ ПОПЛАВКОВОГО ГИРОСКОПА

Реакция поплавкового двухстепенного датчика угловых скоростей на одновременное возмущение со стороны корпуса ракеты – кинематическое возмущение – и проникающее акустическое излучение со стороны маршевых двигателей РН аналитически очерчивается анализом двух уравнений ( первого и второго приближений):

(1)

. (2)

При этом правая часть уравнения (1) явно выражается через параметры углового движения корпуса РН и акустическую вибрацию поверхности поплавка –

.

Или в более полной форме:

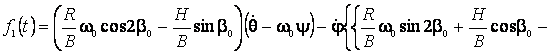
(3)

,

где - производная от угла поворота вокруг оси чувствительности прибора.

Правая часть уравнения (2) выражается как через заданные функции качки корпуса РН и акустической вибрации поверхности поплавка, так и через решение уравнения (1). Используя (2), эту зависимость можно представить в виде:

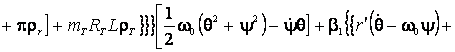
(4)

.

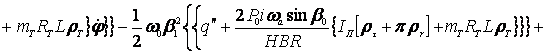
В случае детерминированного процесса задача сводится к определению постоянной составляющей правой части выражения (4). то есть

, (=1,2 – номер приближения)

и систематическая погрешность ДУС определяется формулой –

. (5)

Если же угловое движение корпуса РН и акустическая вибрация поплавка носят случайный характер, то следует говорить о математическом ожидании погрешности прибора. Таким образом,

. (6)

Будем предполагать по аналогии с детерминированными возмущениями, что математические ожидания величин и их производных по времени равны нулю. Математические ожидание произведений этих величин могут содержать постоянные составляющие.

Введем для обозначения математического ожидания величин , , , , и т.д. символы , , , , , . Теперь можно воспользоваться формулой (6) и вычислить погрешность прибора в момент времени . Математические ожидания произведений могут содержать постоянные составляющие. Эти составляющие обозначим символами

и т.д.

Из теории вероятностей известно, что если , то математическое ожидание произведений двух этих функций, вычисленных в разные моменты времени, называется корреляционной функцией связи:

.

Если , то эта функция называется автокорреляционной функцией случайного процесса –

.

При получаем дисперсию случайного процесса :

.

В том случае, когда процесс стационарный, имеем:

;

.

Дисперсия стационарного процесса является величиной постоянной. В дальнейшем не будем предполагать обязательной стационарности процесса.

С учетом сказанного имеем:

Тогда

(7)

Осреднение функции можно получить без труда, если известны корреляционные функции связи встречающихся в (7) комбинаций , , , и .

Применим полученное соотношение для определения сдвига нуля в первом приближении. Для этого следует принять и , то есть предположить отсутствие систематического вращения основания относительно входной оси прибора. Отсюда следуют очевидные равенства:

(8)

Осредненное по времени математическое ожидание сдвига нуля определится по формуле

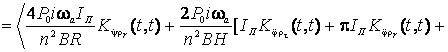
(9)

Используя известные соотношения

выражение (9) можно записать иначе:

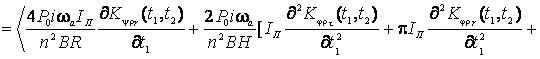
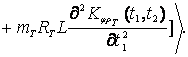(10)

Таким образом, для определения сдвига нуля в первом приближении достаточно знать корреляционные функции связи между углом дифферента (тангажа) и упругими радиальными перемещениями боковой поверхности поплавка , а также между углом рыскания и радиальными и тангенциальными перемещениями боковой поверхности поплавка. Кроме того, должна быть задана корреляционная функция связи между углом рыскания и изгибными колебаниями торца поплавка под действием акустической волны. Эти функции могут быть определены экспериментально.