Экология / 2

Экология / 2. Экологические и метеорологические проблемы больших городов и промышленных зон.

PhD Nemtsova А.А.^*, PhD Ponomarenko E.G.^**

National University of Pharmacy, Ukraine^*

National University of Urban Economy, Ukraine^**

A structured approach to the construction of models of transformation of substances in the aquatic environment

Water quality models are varied and have the different degree of complexity. Balance models and monomolecular models are relatively simple and often used, but they can account only the processes of biochemical decomposition of substances and their income from external sources. When predicting the contents in the aquatic environment substances, which are linked together by processes of mutual transformation, the use of such models is not enough. In this situation, need to build more complex models, which can take account the sequential transformation of substances. The phenomenon of mutual transformation of substances is important for the processes of self-purification and secondary pollution of water bodies. For example, the process of mutual transformation of substances underlies cycles as nitrogen cycle, phosphorus and carbon. Modelling of processes that are more complex requires the analysis of the factors influencing the process, of identifying of their importance and of the possibility to neglect some of them in the process the modelling. The analysis should be based on data of nature observations and be conducted on basis of statistical methods, theory of sensitivity and of factor analysis. After determining the set of significant factors, it is necessary to carry out stages of identification and verification of the model. The final stage is to check the model adequacy. The level of complexity of the model always represents a compromise between the real process and the abstraction of mathematical model. In principle, the components of water quality models can be grouped in the following categories: hydraulic or hydrodynamic, including the processes of transport and mixing of substances in the aquatic environment; chemical compounds; bacteria; phytoplankton and zooplankton; macrophytes and higher trophic levels. The order of these components approximately inversely to the scale knowledge and of ability to describe these processes. Question the model complexity depends on the level of knowledge about the process. From this point of view is preferred, the first three are the most studied component categories: hydrodynamic, chemical compounds and bacteria. However, in some cases it is necessary to include in consideration of the plankton components and higher trophic level. A structured approach to build of model allows to develop and to complicate the model by increasing the level of knowledge about the process.

Consider the use of a structured approach to the construction of mathematical models of water quality on the example of modelling of transformation of nitrogen compounds in the aquatic environment. The main components of the nitrogen cycle are mineral forms of nitrogen in the form of compounds of ammonia nitrogen (NH₄), nitrite nitrogen (NO₂) and nitrate nitrogen (NO₃); nitrogen contained in phytoplankton and zooplankton; organic nitrogen in suspended and soluble forms; free nitrogen and nitrogen of sediments. When modelling the amount of nitrogen in all components is accounted for in terms of pure nitrogen.

The basis of the nitrogen cycle is the nitrification process. It involves the oxidation of ammonia nitrogen to nitrate nitrogen. The nitrification process of the nitrogen takes place in two stages, at both stages is required for aerobic conditions. In the first stage, the oxidation of ammonia nitrogen to nitrite nitrogen is carried out nitrifying bacteria Nitrosomonas. The oxidation reaction takes place exothermically and is described by the equation.

_{In the reaction, on the
one weight part of nitrogen is consumed three weight part of oxygen and
allocated to 54.9 kcal of heat energy. In the second stage, nitrification
bacteria}_Nitrobacter_{oxidize the nitrites to nitrates. The reaction also proceeds
exothermically, but in this case, on the one weight part of nitrogen is
consumed only one weight part of oxygen and allocated to 18 kcal of heat
energy. The reaction equation has the form}

_{Thus, the nitrification
process consumes four weight parts of oxygen per part by weight of nitrogen.
Taking into account atomic weights of nitrogen and oxygen, this means that for
oxidation of 1 mg of nitrogen required is 4.57 mg of oxygen.}

_{For simplicity, below we
consider the dot models of process of the transformation of nitrogen-containing
substances in which all the characteristics of the water body are averaged.}

_{Model 1}_{. The model is a simplified representation of the nitrification process,
namely, the ignored role of bacteria and changes in their density. In this
case, it is assumed that each stage of the nitrification process is first order
reactions. Schematically this process can be represented in the form}

_{A mathematical model,
which describes of nitrification process in aerobic conditions, takes into
account the law of conservation of matter if there is two stages of this
process would be represented in the form}

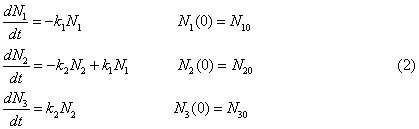
_{where N1, N2, N3 – concentrations of ammonium
nitrogen, nitrite and nitrate in terms of pure nitrogen, mg/l; k1, k2 – decomposition
coefficients of ammonium and nitrite nitrogen, 1/day.; N10, N20, N30 – initial
concentrations of these mineral forms of nitrogen, respectively, mg/l; t – time
of the process of nitrification, days}

_{The system of equations
has a solution}

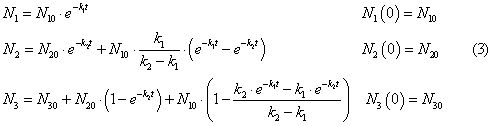
_{The decomposition coefficients
on the results of field observations are taken: for reservoirs k1 = 0.16 1/day,
k2 = 0.28 1/day.; for watercourses k1 = 0,069 1/day, k2 = 10.8 1/day.}

_{Of all mineral forms of
nitrogen, the most strictly standardized content in water nitrite nitrogen.
Therefore, of particular interest is to determine which values can reach its
concentration as result nitrification process. The maximum concentration of
nitrite nitrogen can be determined from the condition}

_{By simple calculations
from the condition (4) can determine the time (tc) during which the
concentration of nitrite nitrogen reached its maximum.}

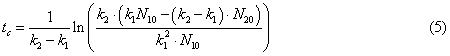
_{In the case where the
nitrite nitrogen formed in the water body only through the transformation of
ammonia nitrogen (N20 = 0), the expression (5) is simplified and the time and value
of maximum concentration of nitrite nitrogen can be determined by the formula}

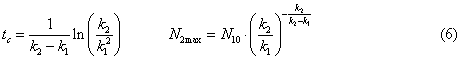
_{According to the
expressions (6), for reservoirs the time during which the concentration of
nitrite nitrogen reaches its maximum, is about five days, and the maximum
concentration of nitrite nitrogen reaches the value of 0.27}_×_{N10. If we assume that the initial content of ammonium nitrogen was at
the upper limit of water quality standard (N10 = 0,389 g/m3), the concentration
of nitrite nitrogen reaches the value of 0,27}_×_{0,389 = 0,105 that exceeds the water quality standard for nitrite
nitrogen, equal to 0,02 g/m3, to 5 times. This calculation shows, how important
is the account of nitrification in the reservoirs when the forecast of water
quality.}

_{For rivers, the picture
is somewhat different. According to the expressions (6) time during which the
concentration of nitrite nitrogen reaches its maximum, is about 0,5 days and
the maximum concentration of nitrite nitrogen reaches 0,006}_×_{N10. In this case, the nitrification process is considerably faster and
the maximum concentration of nitrite nitrogen is significantly less too. If
execute a similar previous calculation for rivers, the maximal concentration of
nitrite nitrogen will equal 0,006}_×_{0,389 = 0,0024, which is almost ten times less than water quality
standard for nitrite nitrogen. This means that for rivers of violation of water
quality only at the expense the process of nitrification will not occur.}

_{The proposed model
adequately describes the process of nitrification for 4 days. Longer forecasts
can lead to considerable error, particularly when predicting nitrate
concentrations.}

_{Model 2.}_{This model is based on the previous model, but allows taking into
account the role of bacteria in the nitrification process.} _{For
this purpose, equations that taking into account the dynamics of changes in
biomass of bacteria, which feed on the considered forms of nitrogen, were
introduced into model. In our case, it is the}_Nitrosomonas_{, feed on ammonia nitrogen, and}_Nitrobacter_{for which a nutrient substrate is nitrite nitrogen. To describe the
change of biomass of bacteria use model Michaelis – Menten – Mono. The equation
of Michaelis – Menten – Mono are the fundamental equations of the theory of
enzyme kinetics, taking into account the peculiarities of development of living
organisms. The biomass of bacteria is quantitatively evaluated by two factors:
the concentration and density of bacteria. The concentration of bacteria
characterizes number of cells per unit volume. The density of bacteria
characterizes the dry weight of bacteria per unit volume. The growth of biomass
usually results in increased cell numbers, cell mass and size of the body.
Because bacteria are unicellular organisms, their biomass increases at the
expense of reproduction. Bacteria grow in the process of dividing into two, so
the rate of growth is the number of doublings per unit time. This value is
called the rate of cell division and is determined by the formula}

_{where, t is
the time of division, N0 – initial concentration
of bacteria, N is the concentration
of bacteria at time t.}

_{The concept of
concentration of bacteria and the speed of their division are commonly used in
studying the cellular structure of living organisms in such Sciences as
biology, genetics, and medicine. In the process of transformation of substances
bacteria play the role of mediator, so it is more convenient to use the notion
of density of bacteria (biomass) and the biomass growth rate. The growth rate
of biomass}_m_{similar to the notion of coefficient of decomposition substance and is
numerically equal to the increase in units of dry mass bacteria per time unit.}

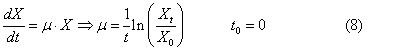_{In conditions of
exponential growth bacteria, the following formula describes link growth rate}_m_{and the rate of cell division}_n_bacteria.

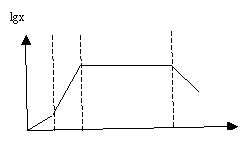_{The exponential growth of bacteria is observed in the most favorable for
their development conditions. It was established experimentally that if there
are no inhibitors that suppress the growth of bacteria, enough of all the
essential nutrients, physic-chemical conditions are suitable for bacteria the
rate of increase of biomass of bacteria is proportional to their biomass. It
means that bacteria grow by exponential low. To ensure favorable conditions
bacteria need regular replenishment of their food base. In the absence of
external coming of the substrate, the biomass goes through 4 phases of
development. This is lag phase (initial phase), log phase (exponential growth),
stationary phase and death phase. Growth curve of the biomass has in this case an
S-shape. The lag phase encompasses the period between the introduction of
bacteria and maximize the speed of their growth. In this phase bacteria adapts
to new conditions and the growth rate increases. Characteristics of the lag
phase depend on the properties of bacteria and the environment. The better the
nutrient medium suitable for bacteria, the shorter the lag phase. Therefore,
the duration of the lag phase describes the suitability of the environment for
the sustenance of bacteria. Ideally, the adaptation occurs almost immediately. Thus,
the duration of the lag phase characterizes the suitability of the environment
for the sustenance of bacteria. Ideally, the adaptation occurs almost immediately.
In reality, the duration of the lag phase may be different. Bacterial culture,
for which the lag phase is missing, is called ideal culture. Than the shorter
lag phase, the bacterial culture closer to the ideal culture. When building
mathematical models for the growth of biomass is assumed that the bacterial
environment is ideal.}

_{The log phase,
corresponding to the exponential biomass development, covers the period of time
when the growth rate of biomass constant and equal to its maximum, that is,}_m₌_m_max_{. The exponential phase is only possible under favorable conditions, the
most important of which is unlimited nutrient substrate and its diversity.}

_{Stationary phase covers
the period when the biomass is constant. The transition from the previous phase
to the stationary phase occurs gradually. First, the decrease substrate for bacteria
and the decrease in living space leads to a decrease in the rate of growth. The
reduction in living space leads to the poisoning of the bacteria by products of
metabolism and negative mechanical impact of the cells on each other. As reducing,
the amount of nutrient substrate the growth rate is reduced from}_m_max_{to zero.} _{During the stationary stage, processes growth of bacteria and their
natural decay are balanced.}

_{The decay phase is
characterized by the excess of the dying away of bacteria in comparison with
their of reproduction. It is the least studied phase. Now concept of the cell
death by exponential low is accepted.}

_{A complex life cycle of
bacteria requires a special approach when modeling. In the basis of models of
the dynamics of biomass of growth is the theory of enzyme kinetics and
principle of minimum. According to this principle, the rate of a complex
reaction is determined by the speed of the slowest simple reaction. Speed other
simple reactions that constitute the mechanism of a complex reaction, are
irrelevant. In relation to bacterial cells, the minimum principle is expressed
by the principle of Liebig. According to the Liebig law, the speed of
development of the organism is determined only limiting factors, that is, those
external factors that are at the minimum. The speed of enzymatic reactions in
the rate-limiting factor is determined by the equation of Michaelis – Menten}

_{where Vmax is the maximum reaction rate; S is the value of the limiting factor;
km is the Michaelis constant, equal to the value of the limiting factor, in
which speed of enzymatic reactions V = 0,5 Vmax.}

_{It is experimentally
proved that the factor limiting the rate of growth of bacterial cells is the
concentration of nutrients. Therefore, the growth of the bacterial mass in
resource-limited settings is determined by the need of the bacteria for
nutrients and the consumption rate of the substrate. The bacteria need nutrients
quantitatively assessed using the economic factor Y. This factor is numerically
equal to the increase in biomass due to the consumption of a unit of substrate
and shows what portion of consumed substrate is used to increase the biomass.}

_{The economic factor is
always less than one or equal to one. When the value Y = 1 the entire substrate
is to increase the biomass, when Y < 1 part of the substrate is lost to
unproductive allocation of metabolic products. Mono shows that under unchanging
external conditions Y = const.}

_{The rate of consumption
of substrate is characterized by a metabolic coefficient or specific rate of
metabolism. Specific metabolic rate q is numerically equal to the amount of
substrate consumed by the unit biomass per unit time.}

_{The value of the
metabolic coefficient and the value of the economic coefficient are linked
relation, which is easy derived from expressions (8), (10) and (11).}

_{From the expression (12)
implies that if the economic coefficient is equal to one, the speed of
processing of the substrate is equal to the biomass growth rate and the entire
substrate is consumed on biomass growth. If the economic factor is less than one,
then the substrate is processed faster than one absorbed by the biomass and the
recycled portion of the substrate is in the form of metabolic products. In
addition, a direct proportionality of metabolic coefficient and growth factor
leads to the fact that metabolic coefficient reaches its maximum simultaneously
with the speed of growth, i.e. exponential growth phase of the biomass.}

_{Applies the principles
of enzyme kinetics for bacteria. In this case, the enzymatic reaction is the
recovery of bacteria of the substrate, the rate of this enzymatic reaction is
the rate of processing of the substrate, that is, metabolic coefficient, and
the limiting factor is the concentration of substrate. If bacteria feed on
several substrates, the limiting factor will be the concentration of a
substrate, which is the minimum. The equation of Michaelis – Menten (9) for the
metabolic coefficient has the form}

_{where ks is
a constant of half-saturation, numerically equal to the substrate concentration
at which the coefficient of metabolism is half of its maximum; S is concentration of limiting
substrate; qmax is the maximum specific rate of metabolism corresponding to the
exponential phase of biomass development.}

_{In models the
transformation of nitrogenous substances, the rate of bacterial growth is of
more concern than the metabolic coefficient, so we write the equation (13)
relative to the speed of bacteria growth. On the base of expression (12) taking
into account, that the economic coefficient is constant under constant ambient
conditions, we obtain the equation of Mono.}

_{Using the expression
(8), (11), (12) and (14), we write the system of equations of the Michaelis –
Menten – Mono, describing the rate of biomass growth of bacteria and consumption
of the substrate depending on the substrate concentration.}

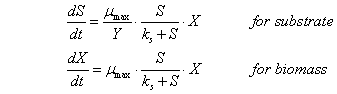
_{Complete the second
equation of the system by the member, taking into account the process of dying
bacteria. Because this process is not limited by the availability of substrate,
it can be assumed that the rate of decay is directly proportional to biomass.
This means that the process of decay of biomass follows the reaction of the
first order. The equation will take the form of}

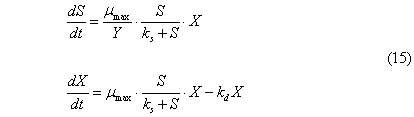
_{We can compose
mathematical model of nitrification process based on model (2) and equations
(15). This model will be taking into account dynamics development of the
nitrifying bacteria. The model diagram presented below}

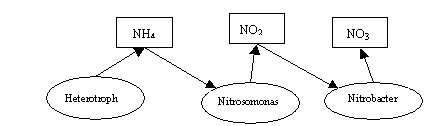
_{In the first stage of
nitrification involves bacteria}_Nitrosomonas_{.
They use ammonia nitrogen as a substrate, and excrete nitrite nitrogen as a
product metabolism.}_Nitrobacter_{bacteria play the main role on the second stage of nitrification. They consume
nitrite nitrogen and produce as a product of the metabolism nitrate nitrogen.
In the model traditionally first written the equations for the substrate, and
then the equations for the biomass of bacteria. The model has the form}

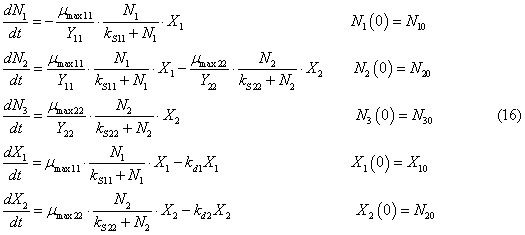
_{where N1, N2, N3, N10, N20,
N30 are concentrations of mineral forms of nitrogen and their initial values,
g/m3; X1, X2, X10, X20 are densities biomass}_Nitrosomonas_and_Nitrobacter_{and their initial values, g/m3;}_m_{max11
is maximum growth rate of}_Nitrosomonas_{when they consume ammonium nitrogen, 1/day;}_m_{max22
is maximum growth rate of}_Nitrobacter_{when they consume nitrogen nitrite, 1/day; Y11 is economic coefficient}_Nitrosomonas_{when they consume ammonium nitrogen; Y22 is economic coefficient}_Nitrobacter_{when they consume nitrogen nitrite; kS11 is constant of half-saturation
for}_Nitrosomonas_{when they consume ammonium nitrogen, g/m3; kS22 is constant of
half-saturation for}_Nitrobacter_{when they consume nitrite nitrogen, g/m3; kd1, kd2 are mortality coefficients
of}_Nitrosomonas_and_Nitrobacter_{, respectively, 1/day}

_{Inclusion in}_modelling_{of nitrification bacteria
has led to a substantial complication of the model. Equation models are
nonlinear, their number increased from two to five; increased the number of
constants which to be need determined in the process model identification from
two to ten. In order to reduce the number of identifiable parameters, the study
of variability of some parameters was performed. The study showed that the
values of parameters such as economic coefficient, the rate of bacterial growth
and constant of half-saturation mainly determined by the type of bacteria,
temperature and pH of the aquatic environment. Because the kind of bacteria
does not change, and the temperature and pH of the aquatic environment vary in
relatively small limits, the six parameters can be excluded from the identification
process of the model. Their values can be taken according to the literature
data. Now it is not}_enough_{information about the process of dying out of the bacteria. We can
assume that the rate of death of bacteria can vary substantially depending on
environmental conditions. Sensitivity analysis the model to this parameter was
used for}_determinate_{necessity to identify the model by the rate of decay of the bacteria. The
results showed that the model is little sensitive to the rate of decay of bacteria,
so parameters kd1 and kd2 may be excluded from the identification procedure.
Usually the values of these parameters are taken kd1 = kd2 =0. Thus, the
procedure for model identification is reduced to determining two parameters –
the initial concentrations of bacteria. The solution of this system of
equations is possible only by numerical methods. Verification of the model
adequacy showed that the model describes well the process within 10 days.}

_{Model 3}_{. This model is based on the model 2. This model permits to take into
account of the role of nitrogen in form dissolved organic matter, nitrogen in
form suspended organic matter and the role of heterotrophic bacteria in
nitrification process. The model diagram presented below.}

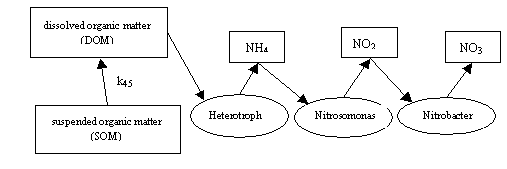
_{In the beginning of the
cycle is lying nitrogen, that included in the composition of suspended organic
matter (SOM). This nitrogen is transformed into nitrogen dissolved organic
matter (DOM). The process consists from two processes: deposition of a part of
the suspended matter in bottom sediments and dissolution of the remaining
portion, and can be evaluated according to the laws of first order reactions. Dissolved
nitrogen is a substrate for}_Heterotroph_{bacteria, which, as a product of metabolism, are isolated in an aqueous environment,
the ammonium nitrogen. Further, the nitrification process is in the previous
scenario. The model consists of eight equations, the first five equations are
inanimate nitrogen compounds, and the remaining three equations describe the
change of biomass of bacteria.}

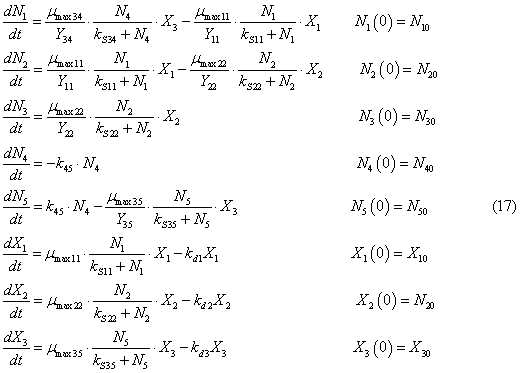
_{where N1, N2, N3, N4, N5, N10, N20, N30, N40, N50 are
concentrations of mineral forms of nitrogen, nitrogen of suspended and
dissolved organic matter and their initial values, g/m3; X1, X2, X3, X10, X20,
X30 are densities biomass}_Nitrosomonas_,_{Nitrobacter,
Heterotroph}_{respectively, and their
initial values, g/m3;}_m_{max11 is maximum growth rate of}_Nitrosomonas_{when they consume ammonium nitrogen, 1/day;}_m_{max22 is maximum growth rate of}_Nitrobacter_{when they consume nitrogen nitrite, 1/day.;}_m_{max35 is maximum growth rate of}_Heterotroph_{when they consume nitrogen of dissolved organic matter, 1/day;
Y11 is economic coefficient}_Nitrosomonas_{when they consume ammonium nitrogen; Y22 is economic coefficient}_Nitrobacter_{when they consume nitrogen nitrite; Y35 is economic coefficient}_Heterotroph_{when they consume nitrogen of dissolved organic matter; kS11 is
constant of half-saturation for}_Nitrosomonas_{when they consume ammonium nitrogen, g/m3; kS22 is constant of half-saturation
for}_Nitrobacter_{when they consume nitrite nitrogen, g/m3; kS35 is constant of half-saturation for}_Heterotroph_{when they consume nitrogen of dissolved organic matter; kd1, kd2,
kd3 are mortality rates of}_{Nitrosomonas, Nitrobacter}_and_Heterotroph_{, respectively, 1/day.`}

_{The study of the model
sensitivity to the new parameters showed that she is very sensitive to changes
in the speed of bacterial growth}_Heterotroph_{.
For example, a decrease in the rate of growth of}_Heterotrophs_{is almost twice as inhibits the growth of nitrates. In addition, there
is the sensitivity of the model to changes in initial biomass density of}_Heterotrophs_{. The increase of this parameter up to 10 times leads to the achievement
of the maximum content of ammonium nitrogen and nitrite nitrogen for a few days
earlier. Overall, this model better describes the nitrification process than
the previous two. Except for the first ten days, the calculated data are in
good agreement with measured data for two months.}

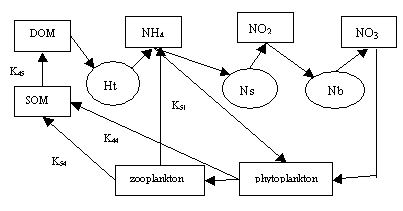_{Model 4}_{. The model includes the model 3, but describes not only the transition
of suspended organic matter in dissolved organic matter, the mineralization and
nitrification of nitrogen containing substances with emphasis on the role of
heterotrophic and nitrifying bacteria, but the role of plankton in the process
of transformation and cycling of nitrogen in the aquatic ecosystem.}

_{Accounting for the role
of zooplankton and phytoplankton has allowed us to close the loop of the
nitrogen cycle in the aquatic ecosystem. The phytoplankton uses for their
growth two types of substrate – ammonia nitrogen and nitrate nitrogen. At the
same time, it is food for zooplankton and, after death, it replenishes the
suspended organic matter. Zooplankton feeds on phytoplankton, in the process of
excretion excretes ammonia nitrogen, when death and defecation restock
suspended organic matter. Since phytoplankton and zooplankton are living
organisms, the processes of their development are subject to the laws of
kinetics Michaelis – Menten – Mono. The processes of decay of both types of
plankton, defecation and excretion of zooplankton obey the law of the first
order. The flow of the products of metabolism of plankton in the form of
dissolved organic matter is insignificant in comparison with other elements of
the nitrogen cycle, so they can be neglected. Since the phytoplankton in the
process of life does not emit products of metabolism, and all of the consumed
substrate (ammonium nitrogen and nitrate nitrogen) is only on the increase in
the biomass of phytoplankton, for him, the economic coefficient is equal to 1. In
this model, phytoplankton and zooplankton play a dual role. On the one hand,
they are live organisms and their growth is subject to the laws of Michaelis -
Menten – Mono. On the other hand, the phytoplankton itself is a substrate for
zooplankton. Both types of plankton in the processes of decay behave as
non-living organisms. With this in mind, the model has the form}

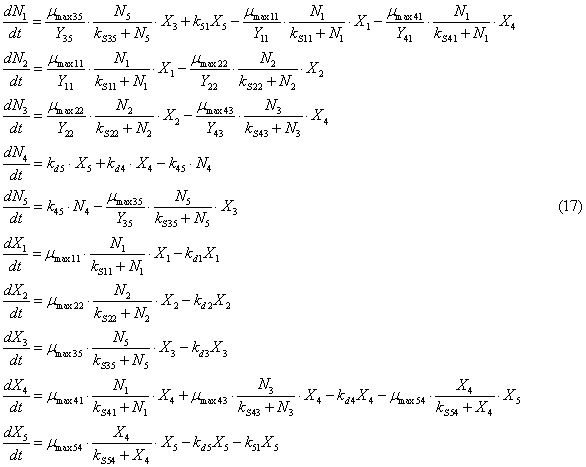
_{Initial conditions: Ni(0)
= Ni0, Xi(0) = Xi0 (i = 1}_¸_5).

_{In the system (17) is
used such new notation: X4, X5, are the densities of biomass of phytoplankton
and zooplankton, g/m3; X40, X50 are the initial densities of the biomass of
phytoplankton and zooplankton, g/m3;}_m_{max41
is maximum growth rate of phytoplankton when he consumes ammonia nitrogen,
1/day;}_m_{max43 is maximum growth rate of phytoplankton when he consumes nitrogen-nitrate,
1/day,}_m_{max54 is maximum growth rate of zooplankton when he consumes phytoplankton,
1/day; Y41 is the economic coefficient of phytoplankton when he consumes ammonia
nitrogen; Y43 is the economic coefficient of phytoplankton when he consumes nitrate
nitrogen; Y54 is the economic coefficient of zooplankton when he consumes phytoplankton;
kS41 is constant of half-saturation for
phytoplankton in nutrition by ammonium nitrogen, g/m3; kS43 is constant of half-saturation
for phytoplankton in the diet of nitrate nitrogen, g/m3; kS54 is constant of half-saturation
for zooplankton when feeding on phytoplankton; kd4, kd5 are mortality rates of
phytoplankton and zooplankton, 1/day; k51 is a coefficient of excretion of
zooplankton, 1/day. The values of economic coefficients Y41 = Y43 = 1.}

_{The proposed model is
complex, but it describes well the simulated process and is adequate for the
period in a few months. The drawback of the previous model, which is manifested
in the deviation of calculated data from field during the first ten days, in
the model is neutralized.}

_{The drawback of all
considered models is that they do not take into account the spatial
characteristics of the water body. Such models are good to use for bodies of
water with strong mixing conditions. In other cases, it is necessary to modify
the proposed model by using the turbulent diffusion equation or the equation of
convective transfer.}