Экономические науки/13.Региональная экономика

Студент. Чепухалина К.А

Тихоокеанский государственный университет, Россия

Методы оценки инновационного потенциала региона с использованием корреляционно-регрессионного анализа

Инновационный потенциал - это не только возможность создания новшеств, осуществления инноваций, но и готовность воспринять эти нововведения для последующего эффективного использования на уровне, соответствующем мировому.

Величина инновационного потенциала является параметром, позволяющим оценить возможности инновационной деятельности и определить стратегию инновационного развития. От состояния инновационного потенциала зависят управленческие решения по выбору и реализации инновационной стратегии, в связи с чем возникла необходимость его комплексной оценки как сложной системы.

Нередко предлагаемые методики оценки инновационного потенциала не учитывают его структуры, поэтому анализ получается неполным.

Как правило, инновационный потенциал региона состоит из системы потенциалов:

- производственно-технологического потенциала;

- кадрового потенциала;

- информационного потенциала;

- финансового потенциала;

- научно-технического потенциала;

- организационного потенциала;

- управленческого потенциала;

- инновационной культуры;

- потребительского сегмента потенциала.

В российской практике традиционно сложились несколько подходов к оценке инновационного потенциала региона.

1. Рейтинговый подход основан на процедуре интегрирования индикаторов, отражающих важнейшие аспекты инновационной составляющей социально-экономического развития региона.

2. Нормативный подход, позволяющий с помощью комплекса показателей и шкалы их измерения проследить за развитием инновационного процесса.

3. Подход, базирующийся на определении интегрального инновационного потенциала региона, опирается на метод главных компонент, а также на корреляционно-регрессивный анализ.

Объектами статистического изучения в экономических науках являются сложные системы. В данной работе нас интересует, такая модель уравнений, когда результирующий признак Y одного уравнения может выступать в виде фактора Х в другом уравнении.

Таким образом, параметры системы одновременных уравнений примут следующее значение:

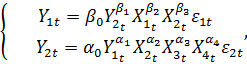(1)

В качестве показателей, характеризующих инновационный потенциал региона были выбраны: - объем валового регионального продукта; - объем инновационных товаров, работ, услуг; - среднегодовая численность занятых; - объем инвестиций в основной капитал; - затраты организаций на технологические инновации; - число персонала, занятого научными исследованиями и разработками; - параметры производственной функции; - случайная величина, характеризующая отклонение реального значения результативного признака от теоритического, найденного по уравнению регрессии.

Корреляционная матрица исследуемых факторов представлена в табл.1., построена на основе статистических данных по Дальневосточному федеральному округу.

Таблица 1

Результаты расчета корреляционной связи исследуемых факторов

Наименование факторов	- ВРП (млн. руб)	- Среднегодовая численность занятых (тыс.чел)	- Объем инвестиций в основной капитал (млн.руб)	Затраты на технологические инновации (млн.руб)	-Число персонала, занятого исследованиями (тыс.чел)	- Объем инноваци онных товаров, (млн.руб)
- ВРП (млн. руб)	1
- Среднегодовая численность занятых	0,6959	1
-Объем инвестиций в основной капитал	0,9818	0,7841	1
-Затраты на технологические инновации (млн.руб)	0,6839	0,4435	0,6815	1
-Число персонала, занятого исследованиями (тыс.чел)	-0,8193	-0,7513	-0,8413	-0,7687	1
- Объем инновационных товаров (млн.руб)	0,7484	0,3583	0,6852	0,5189	-0,4130	1

Проанализируем полученные коэффициенты корреляции с помощью шкалы Чеддока.

Заметим, что функциональная связь обозначается 1, а отсутствие связи-0. Как мы видим, зависимость результативного признака Y от среднегодовой численности занятых и затрат на технологические инновации является средней, а объем инновационных товаров проявляет высокое влияние. Очень высокое влияние на объем ВРП демонстрирует объем инвестиций в основной капитал. Однако существует один фактор оказывает обратное вяление на объем ВРП, это число персонала, занятого исследованиями, т.е при увеличении персонала, уменьшается объем ВРП.

Далее мы предлагаем провести регрессионный анализ с использованием режима Регрессия MS Excel и вследствие этого построим уравнение регрессии с пятью влияющими факторами:

(2)

где a- параметры (коэффициенты) регрессии, x- влияющие факторы, k (1,2,3,4,5)-количество факторов модели.

Полученные результаты по регрессионной статистике, представлены в табл.2.

Таблица 2

Результаты регрессионного анализа

Регрессионная статистика
Множественный R	0,992871495
R-квадрат	0,985793806
Нормированный R-квадрат	0,973955311
Стандартная ошибка	96895,82425
Наблюдения	12

Рассмотрим представленную в таблице 2 регрессионную статистику. Величина R-квадрат, называемая также мерой определенности, характеризует качество полученной регрессионной прямой. Это качество выражается степенью соответствия между исходными данными и регрессионной моделью. Данный показатель не может быть больше 1 и считается неплохо, когда R² выше 0,8, а если меньше 0,5, то резонность такой модели можно смело ставить под большой вопрос. В нашем случае мера определенности равна 98,57%, что говорит о высоком качестве данной модели.

Значение критерия Fфакт составило 83,27, а Fтабл = 4,39, следовательно, можно смело утверждать, что факторный признак существенно, надежно оказывает влияние на признак-результат т.е различие в изменчивости индекса роста ВРП под воздействием рассматриваемых факторов можно считать существенным.

Для построения уравнения регрессии, требуется изучить коэффициенты представленные в табл.3.

Таблица 3

Коэффициенты регрессии

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение	11675866,1	4963258,818	2,352459649	0,056866949
Переменная X 1	-2688,282823	1321,091897	-2,034894643	0,088064801
Переменная X 2	1,650550601	0,251208572	6,570439006	0,000595848
Переменная X 3	-2,194099732	2,494980976	-0,879405395	0,41301199
Переменная X 4	-137,8853456	108,0645208	-1,275953889	0,249138201
Переменная X 5	0,620831419	0,364733875	1,702149052	0,139624775

11675866,1--коэффициент, который показывает, какой будет Y в случае, если все используемые в модели факторы будут равны 0, подразумевается что это зависимость от других неописанных в модели факторов;

-2688,28--коэффициент, который показывает величину влияния фактора -на Y. То есть влияние среднегодовой численности занятых в экономике на объем валового регионального продукта. Увеличение среднегодовой численности занятых в экономике приводит к уменьшению ВРП.

1,65--коэффициент влияния объема инвестиций в основной капитал на величину объема валового регионального продукта. То есть увеличение объема инвестиций в основной капитал, влечет за собой увеличение объема ВРП.;

-2,19--коэффициент влияния затрат на технологические инновации на величину объема валового регионального продукта, имеет отрицательное влияние.

-137,88--коэффициент влияния численности персонала, занятого научными исследованиями и разработками на объем валового регионального продукта, здесь так же наблюдается отрицательное влияние.

0,62--коэффициент влияния объем инновационных товаров, работ, услуг на объем валового регионального продукта, здесь так же наблюдается положительное влияние.

Соберем рассчитанные коэффициенты в модель:

Y = 11675866,1-2688,28x₁+1,65x₂-2,19x₃-137,88x₄+0,62x₅ (3)

При помощи этого уравнения переменная Y выражается через константу a и угол наклона прямой (или угловой коэффициент) b, умноженный на значение переменной X. Константу a также называют свободным членом, а угловой коэффициент - коэффициентом регрессии или B-коэффициентом.

В большинстве случав (если не всегда) наблюдается определенный разброс наблюдений относительно регрессионной прямой.

Уравнение регрессии показывает, каким будет среднее значение результативного признака У при том или ином значении факторного признака Х, если остальные факторы, влияющие на У и не связанные с Х, не учитывать, т. е абстрагироваться от них.

На основании данной модели можно предположить, что затраты на наращивание инновационного потенциала имеют отложенный эффект и не приводят к росту ВРП немедленно, после их осуществления. Наличие такого временного лага необходимо учитывать при разработке инновационной стратегии развития региона и формирования долгосрочной инвестиционной политики.

Литература

[1] Александрова Е.Н., Салмина О.А. Методические подходы к оценке эффективности функционирования инновационной сферы на макроуровне. // Фундаментальные исследования.-2014.-№6-С.120-123

[2] Зарецкая, В. Г.Построение производственной функции региона с учетом инновационной составляющей / В. Г. Зарецкая, Л. А. Дремова, Л. М. Осиневич // Региональная экономика: теория и практика.-2014.-№ 2.-С.20-28.

[3] Добров, Г.М. Научно-технический потенциал: структура, динамика, эффективность / Г.М. Добров, В.Е. Тонкаль, А.А. Савельев и др.-Киев: Наукова думка, 2014.-347с.

[4] Дворецкий С.И., Матвейкин В.Г., Минько Л.В., Таров В.П., Чайникова Л.Н., Летунова О.И. Инновационный потенциал: современное состояние и перспективы развития: монография – М.:«Издательство Машиностроение-1», 2013.-9-10с.

[5] Статистический сборник «Регионы России. Социально-экономические показатели» {Электронный ресурс] //URL:http://www.gks.ru/wps/wcm/connect/rosstat_main/rosstat/ru/statistics/publications/catalog.html. (дата обращения 29.02.2016)

[6] Инновации. Официальный портал Правительства Хабаровского края: {Электронный ресурс] //URL: https://khabkrai.ru/ (дата обращения 12.03.2016)

[7] Изобретательская активность в регионах Российской Федерации: {Электронный ресурс] // URL: http://ipc-rm.narod.ru/izobr_act_reg.doc (дата обращения 01.03.2016)