УДК 004.383:656.056
Алдибекова К.А., магистр технических наук
Преподаватель
лицея при КазГАСА
Распознавание
образов методом SURF
В данной
статье рассматривается актуальность системы
распознавания образов методом SURF,
позволяющая идентифицировать объект или определения его свойств. Приведены доказательства того, что система может применяться для сравнения изображений, поиска
объектов на изображениях, 3D реконструкции.
Бұл мақалада
бейнені анықтау үшін немесе оның қасиеттерін
анықтауға мүмкіндік беретін Surf әдісі арқылы тану жүйесінің өзектілігін
талқылайды. Жүйе бейнелерді салыстыратын дәлелдер, бейне
объектілерін іздеу, 3D қайта құру үшін пайдаланылуы
мүмкін.
This article discusses the relevance of the pattern recognition system
by SURF, allowing to identify the object or to determine its properties. Proofs
that the system can be used to compare images search for objects in images, 3D
reconstruction.
Распознавание
образов (объектов, сигналов, ситуаций, явлений или процессов) - задача
идентификации объекта или определения каких-либо его свойств по его изображению
(оптическое распознавание) или аудиозаписи (акустическое распознавание) и
другим характеристикам.
Общая
структура системы распознавания и этапы в процессе ее разработки показаны на
рисунке 1.
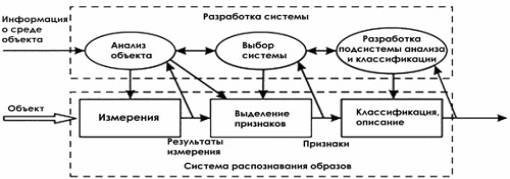
Рисунок 1- Структура системы
распознавания
Задачи
распознавания имеют следующие характерные черты.
Это
информационные задачи, состоящие из двух этапов:
- преобразование исходных данных к виду, удобному
для распознавания;
- собственно распознавание (указание
принадлежности объекта определенному классу).
Метод обнаружения пешеходов метод SURF. Метод может применяться
для сравнения изображений, поиска объектов на изображениях, 3D
реконструкции.
Задача
распознавания образов до сих пор не решена в полном объеме. Однако, в рамках
существенных ограничений, есть методы, позволяющие приблизится к ее решению.
Среди
различных родственных методов, был выбран для рассмотрения метод Speeded Up
Robust Features (SURF), поскольку он является одним из самых эффективных и
быстрых современных алгоритмов. Кроме того, SURF является распространенным
методом, его реализации есть во многих математических библиотеках.
Обзор метода SURF. SURF решает две задачи –
поиск особых точек изображения и создание их дескрипторов, инвариантных к
масштабу и вращению. Это значит, что описание ключевой точки будет одинаково,
даже если образец изменит размер и будет повернут (здесь и далее мы будем
говорить только о вращении в плоскости изображения). Кроме того, сам поиск
ключевых точек тоже должен обладать инвариантностью. Так, что бы повернутый
объект сцены имел тот же набор ключевых точек, что и образец.
Метод
ищет особые точки с помощью матрицы Гессе.
Детерминант
матрицы Гессе (т.н. гессиан) достигает экстремума в точках максимального
изменения градиента яркости. Он хорошо детектирует пятна, углы и края линий.
На рисунке 3 – особые точки изображения здания,
найденные с помощью матрицы Гессе.
Диаметр круга показывает масштаб особой точки. Зеленая линия –
направление градиента яркости.

Рисунок
3 - Особые точки изображения здания,
найденные с помощью матрицы Гессе
Гессиан
инвариантен относительно вращения. Но не инвариантен масштабу. Поэтому SURF
использует разномасштабные фильтры для нахождения гессианов.
Для
каждой ключевой точки считается направление максимального изменения яркости
(градиент) и масштаб, взятый из масштабного коэффициента матрицы Гессе.
Градиент
в точке вычисляется с помощью фильтров Хаара.
После
нахождения ключевых точек, SURF формирует их дескрипторы. Дескриптор
представляет собой набор из 64(либо 128) чисел для каждой ключевой точки. Эти
числа отображают флуктуации градиента вокруг ключевой точки (что понимается под
флуктуацией — рассмотрим ниже). Поскольку ключевая точка представляет собой
максимум гессиана, то это гарантирует, что в окрестности точки должны быть
участки с разными градиентами. Таким образом, обеспечивается дисперсия
(различие) дескрипторов для разных ключевых точек.
Флуктуации
градиента окрестностей ключевой точки считаются относительно направления
градиента вокруг точки в целом (по всей окрестности ключевой точки). Таким
образом, достигается инвариантность дескриптора относительно вращения. Размер
же области, на которой считается дескриптор, определяется масштабом матрицы
Гессе, что обеспечивает инвариантность относительно масштаба.
Флуктуации
градиента также считаются с помощью фильтра Хаара.
Интегральное представление.
Для
эффективного вычисления фильтров Гессе и Хаара – используется интегральное
представление изображений.
Если
кратко, то интегральное представление является матрицей, размерность которой
совпадает с размерностью исходного изображения, а элементы считаются по
формуле:
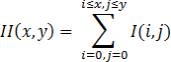 ,
,
где, I(i,j) – яркость пикселов исходного
изображения.
Имея интегральную матрицу можно очень быстро
вычислять сумму яркостей пикселов произвольных прямоугольных областей
изображения, по формуле:
SumOfRect(ABCD)
= II(A) + II(С) — II(B) —
II(D), где, ABCD – интересующий нас прямоугольник.
Заключение
Методы распознавания образов позволяют решать задачи
классификации, прогноза и управления процессами и сложными системами, а также
принятия в заданных условиях наиболее рациональных решений, основанных на опыте
прошлого. Обычно решение такого рода задач производится специалистом в данной
конкретной области. В связи с ростом сложности изучаемых систем и процессов,
при исследовании которых необходимо принимать во внимание большое число
взаимосвязанных случайных факторов, возникает проблема повышения объективности
и правильности принимаемых решений.
Возможность математической постановки ранее не
формализованных и
решающихся на интуитивном уровне задач обусловила важность и
перспективность применения методов распознавания широким кругом специалистов:
математиками, инженерами, социологами, геологами, медиками и т.д.
Несмотря на большое разнообразие методов и подходов к
распознаванию образов, в настоящее время не существует единого универсального
алгоритма, позволяющего решить задачу классификации объектов.
Среди возможностей системы должны быть: распознавание
пешеходов, простота работы с видеофайлами.
Список использованной
литературы
1. Журавлев Ю.И. Об алгебраическом подходе к
решению задач распознавания или классификации // Проблемы кибернетики. М.: Наука, 2005. - Вып. 33. С. 5-68.
2.
Ryuji Funayama, Hiromichi Yanagihara, Luc Van Gool, Tinne Tuytelaars, Herbert
Bay, "ROBUST INTEREST POINT DETECTOR AND DESCRIPTOR", published
2009-09-24
3.
N. Dalal and B. Triggs. Histograms of oriented gradients for human detection //
Conference on Computer Vision and Pattern Recognition (CVPR), 2005.
4.
D. Geronimo, A.M. Lopez, A.D. Sappa, and T. Graf. Survey of pedestrian
detection for advanced driver assistance systems // Pattern Analysis and
Machine Intelligence, 2010.
5. «Теория распознавания образов (статистические
проблемы обучения)», В. Н. Вапник, А. Я. Червоненкис. Издательство «Наука»,
Главная редакция физико-математической литературы, М., 1974, 416 стр.