Sukhorukova Irina V., Doctor of Economics, Professor of the Mathematics Department of the Russian Plekhanov University of Economics, 117997, Russian Federation, Moscow, Stremyanniy per., 36;

 

Mushrub  Vladimir A.,  Ph.D , associate professor of the Academic Department of Mathematical Methods in Economics of the Russian Plekhanov University of Economics, 117997, Russian Federation, Moscow, Stremyanniy per., 36.

 

The Jacobson Radical and ring Endomorphisms.

 

Throughout this paper all rings are associative but not necessarily contain a unity and R denotes such a ring unless indicated otherwise. Let f be an endomorphism of R. We say that an ideal I of R is an f-ideal if . An ideal I of R is called invariant with respect to f (or briefly f-invariant) if f(I)  I.

In this paper we are concerned about the question of determining the behavior of the Jacobson radical when it is mapped by ring endomorphisms. We will find conditions that ensure that the Jacobson radical of R is an f-ideal.

It is well known that the abstract definition of a radical property ρ in the category of rings includes the following axiom:

if φ:R  S is a surjective homomorphism of rings then φ(ρ(R))  ρ(S).

On the other hand, any radical τ in the category of right R-modules satisfies in particular the following axiom:

if φ:M  N is a homomorphism of R-modules then φ(τ(M))  τ(N).

 

Therefore, it seems interesting to know under which circumstances the inclusion f(ρ(R))  ρ(R) holds true, where f : R  R is an endomorphims of R.

This problem cannot be solved rashly and simultaneously for various radicals by abstract radical theory methods. For each specific radical, this problem should be considered individually.

 

We can formulate only one obvious assertion of common type:

Lemma 1. Let R be a ring and f be an endomorphism of R with Ker f  ρ(R) and ρ be a radical property in the category of all associative rings.

(1). If ρ is a strongly hereditary radical (i.e. every subring of any ρ-radical ring is ρ-radical), then (ρ(R))  ρ(R).

(2). If ρ is a strict radical (i.e. it’s semisimple class is closed under taking subrings, see [16]), then f (ρ(R))  ρ(R).

Proof. (1). Since S = f((ρ(R))) is a subring of ρ(R), S is ρ-radical. But (ρ(R)) / (Ker f (ρ(R))) is ρ-radical, because of the isomorphism S (ρ(R)) / (Ker f (ρ(R))). Then since ρ(R) /  (Ker f  (ρ(R))) and Ker f (ρ(R)) are both ρ-radical, the ideal  (ρ(R)) is ρ-radical too.

Let P = ρ(R). Then f(P) / Pf(P) is ρ-semisimple as a subring of R / P and  f(P) / Pf(P) is ρ-radical as a homomorphic images of P. Hence f(P) / Pf(P) = 0 and f(P) P.

 

Throughout the sequel, except for Proposition 1, let R be an associative ring and let us denote by J=Rad(R) its Jacobson radical.

What interests us in this work is invariance of the Jacobson radical. The question that naturally arises is:

Question 1. On what conditions R and f does one of the relations , ,  hold true?

This problem was first considered by A.V. Jategaoncar, who proved that the Jacobson radical of a right Artinian ring R is invariant with respect to any injective endmorphism of the ring R.

We call the problem described above as the problem on invariance of classical radicals of rings with respect to their endomorphisms. Under certain additional hypotheses on R and f, such as R is a right Kasch ring and f is an injective endomorphism, we also give the affirmative answer to Question 1, see Theorem 1.

The authors of the present paper have received different results concerning this problem. Some of them are presented in Propositions 2 and Theorems 1. Proposition 1 deals with universal algebra by the reason that it can be used not only in the associative rings, but also for other algebraic structures such as groups, semigroups, division rings, alternative rings.

 

In particular, the following problem looks natural to state:

Question 2. Is the Jacobson radical of SBI-ring R invariant with respect to injective endomorphisms of R?

With certain additional assumptions, the answer is yes. However there are many obvious counterexamples of SBI-rings having an injective endomorphism f such that. Some partial affirmative answers to this question will be given in [3].

 

Invariance of the nil radical with respect to endomorphisms was used to determine radicals of skew polynomial rings, their ring of fractions (see [1]), and Goldie dimension (see [2]). The result of the research could be an effective technique for investigating structure of skew polynomial rings, Cohn-Jordan extensions of rings, skew group rings and skew semigroup rings.

Research carried out at Plehanov Russian University of Economics.

 

Here is a piece of notations: a set of non-negative integers is denoted by , the right and left annihilators of M in R are denoted by r(M) and , in the commutative case the annihilator of M  is denoted by ann(M).

First we give the following proposition.

Proposition 1. Let R be a universal algebra,  f  be an endomorphism of R and S be a nonempty set of subalgebras of R. Set  is a subset of S}, i.e.  is the set of all kinds of intersections of some subalgebras . Set I = . Suppose that one of the following conditions (1.1) and (1.2) holds true:

(1.1) each nonempty subset  îf Ω contains an inclusion-wise maximal element;

(1.2) I =  for every infinite subset  of Ω.

Suppose in addition that R satisfies also the following condition:

(1.3) given any subalgebra , there exists subalgebra  such that .

Then  .

Proof. Inductively, we can construct the sequence {  } as follows:  = S and  . Set  for all n ∈ . Then , since S = . Since any subalgebra M  S can be represented as M =  for some , we have . It implies that  .

Note that . Therefore, it can be proved by induction on n that  for all nonnegative integers n. It follows from  that .

First suppose that condition (1.1) holds true. Since all algebras  belong to Ω, the ascending chain  by condition (1) must stabilize, so, for some m, . It implies that . Hence and  .

Let us suppose now that condition (1.2) holds true. If the set S is finite, then the condition (1.1) holds true. So, without loss of generality, we may assume that S is an infinite set. It is easy to see that the set  in this case is infinite too. Condition (1.2) yields . Thus  .

 

First let us recall the notion of quasiregularity. An element a  is said to be right quasi­regular if a + x – ax = 0 for some element x of R. An element a  is quasi­regular if it is both left and right quasi­regular. If every element of a right ideal P of R is quasiregular (right quasi­regular), then P is called quasi­regular (resp. right quasiregular).

Recall that a right ideal M of R is called regular (or modular) if there exists an element e in R such that er − r ∈ I for all r ∈ R. This element e is called a left unity modulo I. Any right regular ideal contains in maximal regular right ideal with the same left unity. If R contains the unity 1 then any right ideal of R is regular, since we may set e = 1. Recall that the Jacobson radical J=Rad(R) of R can be defined as the intersection of all maximal regular (modular) right ideal of R. The Jacobson radical J=Rad(R) of R is also called quasi-regular radical, because Rad(R) is just the largest right quasiregular right ideal of R.

We use Sp(Rad(R)) to denote the set of all maximal regular right ideals of R.

 

Definition 1. Let f be an endomorphism of R. Following D. Jordan we say that a right ideal I ring R is weakly f-closed if I =  The right ideal I is said to be f-closed if I is weakly -closed for all natural numbers n. Analogously an ideal I ring R is said to be weakly f-closed in I =  An ideal I is called f-closed if, for all natural numbers n, I is weakly -closed.

Let us denote by  the ring  obtained from R by adjoining a unity.

 

Proposition 2. Let f be an endomorphism of R such that . Let J be the Jacobson radical of R. Let S = Sp(Rad(R)) be the set of all maximal regular right ideals of R. Set   Sp(Rad(R))}. Suppose that one of the following conditions (2.1)and (2.2) holds true:

(2.1) every subset  îf  contains a maximal element;

(2.2) J = , for every infinite subset  of Ω.

In additoin let us suppose that the following condition (2.3) holds true:

(2.3) all maximal regular right ideals of R are weakly f-closed.

Then  

Proof. Let us use Proposition 1 with I = J and S = Sp(Rad(R)). If I = J then condition (1.1) implies (2.1) and condition (1.2) coincides with condition (1.1) of Proposition 1 for the case considered. Thus Proposition 2 follows from Proposition 1 provided that the condition (1.3) holds true in the case under consideration. So to prove the present proposition, it is sufficient to prove that for each  Sp(Rad(R)) there exists a subalgebra  Sp(Rad(R)) such that  .

Let M  and e be a left unity modulo M. Let us denote by P the smallest right ideal of R containing f(M), i.e. P =  . If  and  then f(e)f(t)c −f(t)c = (f(e)f(t) −f(t))c  . Since  every element s of R can be represented as 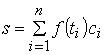 where  and  . Therefore f(e)s −s  for all  . Moreover, since  is weakly f-closed,  . It follows that P is a proper regular right ideal of R, f(e) is a left unity modulo P and consequently f(e)  P. So there exists a maximal regular right ideal N of R such that P  N, f(e)  N and f(e) is a left unity modulo N.

To finish the proof we observe that  and e , since f(e)  N. Moreover, er – r ∈  for all r ∈ R, i.e. e is a left unity modulo  and  is regular. However,  is a maximal regular right ideal of R, so, indeed, . Hence the condition (1.3) of Proposition 1 is satisfied. The present proposition immediately follows.

 

Definition 2. A ring R is called a right Kasch ring if every maximal regular right ideal of R coincides with the right annihilator of some nonempty subset S of R.

 

Lemma 2. Let f be an injective endomorphism of R and L be a subset of R Then  = {r  Lr = 0} is an f-closed ideal of R.

Proof. Let . To prove the inclusion   let a  , b  and c . Since  =  =  = 0, we obtain that  = 
=  and consequently Lc = 0. The reverse inclusion   is obvious.

 

We state a major result.

Theorem 1. Let R be a right Kasch ring and f be an injective endomorphism of R such that  . Suppose that one of the following conditions (i), (ii) holds true:

(i) R satisfies the ascending chain condition for right annihilators containing J;

(ii) J = , for every infinite subset  of Sp(Rad(R)).

Then  

Proof. It is clear that (ii) implies (2.2). In order to prove the implication "(i)(2.1)" we need to make sure that the intersection  is a right annihilator in R if  Sp(Rad(R)). Finally, by using Lemma 2 we can see that every maximal regular right ideal of the ring R is f-closed. Hence, for every maximal regular right ideals of R, the condition (2.3) of Proposition 2 is also satisfied and theorem 1 follows from Proposition 2.

 

Example 1. There exists a commutative Kasch ring satisfying both conditions (i) and (ii) of theorem 1 the Jacobson radical of which is neither zero nor nil.

Proof. Let K be a commutative principal ideal domain with unity. As well-known every prime ideal of K is a maximal ideal of K. Let S be the set of all maximal ideals of K. Consider the power series ring T = K[[x]] in one variable x over K. If P∈S then M(P) denotes the simple T-module T/(P+xT) that is isomorphic to K/P as a K-module. We set R=T  where M =  M(P) and define multiplication on R by setting

(t+m)(s+n)=ts+(tn+sm)  (  t, s ∈R  m, n ∈M).

Then R becomes a commutative ring with the same unity (1 + 0) = 1 as in K. It is transparent that J(R)=J(T)  J(K)  xT  M, here we consider K and T as subrings of R. Note that R/J(R)  K/J(K) is a commutative Noetherian ring. Hence R satisfies condition (i) of Theorem 1.

Since K is a principal ideal domain, given any infinite subset Γ of S, we have J(K) = . But every maximal ideal of R has the form of P+J(R)=P  xT  M=ann(M). It is straightforward to check that R satisfies condition (ii) of Theorem 1. Note in addition that  for every unitary endomorphism of R.

We finish this paper by formulating the following conjecture.

Conjecture. Let R be a semilocal SBI-algebra over a field k and 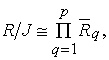 where 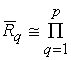 Matrix(  ) are the matrix rings over some division rings Dq. If Ker fJ and the Gelfand-Kirillov transcendence degree of all Dq over the base field k are finite, then .

 

Bibliography

1. Grishin A.V., Mushrub V.A., Schigolev V.V., Tsybulya L.M., Platonov S.V., “Varieties of Algebras, T-Spaces and Application of algebraic Groups to them”, research report ¹ 07-01-00625 (Russian Foundation for Basic Research), 2009.
(Grishin A.V., Mushrub V.A, Schigolev V.V., Tsibulya L.M., Platonova S.V., “MNOGOOBRAZIYA ALGEBR, T-PROSTRANSTVA I PRIMENENIE K NIM ALGEBRAIChESKIH GRUPP”, otchet o NIR # 07-01-00625 (Rossiyskiy fond fundamentalnyih issledovaniy), 2009.

 

2. V. A. Mushrub, On the uniform dimension of skew polynomial rings in many variables, Fundam. Prikl. Mat., 2001, Volume 7, Issue 4, 1107–1121, pp. 1107-1121. (Mushrub V.A. O razmernosti Goldi rasshireniy Ore so mnogimi peremennyimi //Fundamentalnaya i prikladnaya matematika., 2001. T. 7, vyip. 4, C.1107-1121.)

 

3.       I. V. Suhorukova, V.A. Mushrub, Invariance of the Jacobson Radical of SBI-rings with respect to endomorphisms. To appear.