К.т.н. Лукащук Т.І., Буров О.В., Жаган Ю.А.

Харківський національний автомобільно-дорожній університет

Методи математичного програмування як сучасні вектори інтелектуального розвитку майбутніх фахівців

Математична підготовка майбутніх фахівців у вищій школі складається з вивчення основних понять та методів багатьох математичних дисциплін: вищої алгебри, аналітичної геометрії, математичного аналізу, де розглядаються елементи диференціального та інтегрального числення, диференціальних рівнянь, елементів теорії ймовірностей та математичної статистики. Важливою математичною дисципліною при підготовці фахівців для народного господарства держави – економістів, менеджерів, фінансистів, є математичне програмування. При вивченні цієї дисципліни студенти навчаються будувати математичні моделі технологічних процесів та шукати оптимальні розв’язки поставлених задач.

В курсі «математичне програмування» розглядаються методи лінійного програмування, нелінійного та динамічного програмування і таке інше [1, 2].

Фундаментальна математична підготовка студентів має своїм основним завданням вивчення методів класичних математичних дисциплін. Математичне програмування, як математична дисципліна, відноситься до прикладної математики і, на жаль, на вивчення цієї дисципліни відводиться небагато часу. В цьому разі постають методи знайомства з можливостями цієї дисципліни такі як факультатив або самостійна робота по пошуку оптимального розв'язку конкретної економічної задачі. Для постановки задач та пошуку оптимального розв'язку конкретної економічних задач викладач-математик має співпрацювати з викладачами-економістами. На цьому етапі підготовки фахівців є деякі протиріччя. Елементи та можливості математичного програмування студент вивчає на молодших курсах: першому або другому, залежно від фаху, а економіку студенти вивчають на старших курсах. Розв’язком цих протирічь можуть бути доповіді на студентських наукових конференціях, де студенти доповідають про результати впровадження методів математичного програмування, для пошуку оптимальних розв'язків деяких економічних задач, наближених за фахом до майбутньої спеціальності. Це збагачує інтелектуально майбутнього фахівця, надає йому впевненості в собі та підвищує якість навчального процесу.

В даній роботі наведено приклад укладання оптимального плану перевезень вантажів залізної руди на металургійні комбінати. В загальному вигляді є декілька пунктів виробництва А_і та декілька пунктів споживання В_j. Якщо відомі об’єми виробництва сировини та потреби виробництва, а також відома вартість перевезення одиниці вантажу з пункту А_і до пункту В_j на одиницю відстані С_іj, то можна скласти оптимальний план перевезень, вартість перевезення якого є найменшою. В загальному виді така задача називається транспортною.

Математична модель транспортної задачі має вигляд, наведений у таблиці 1.

Таблиця 1.

Вj Аі	В1=100	В2=150	В3=250	В4=80	В5=120
А1=200	10	8	200 7	12	9
А2=300	100 7	9	10	80 13	120 6
А3=170	12	120 7	50 8	9	10
А4=30	13	30 6	9	10	12

Постачальниками в таблиці 1 позначені гірничо-добуваючі підприємства України по розробці уранових та марганцевих руд підземним та наземним способами під позначками: А₁ – Криворізький гірничо-збагачувальний комбінат; А₂ – Кременчуцький залізорудний район; А₃ – Нікопольський марганцеворудний басейн; А₄ – Павлоградський гірничий комбінат.

Виробниками в даній роботі визначені металургійні виробництва: В₁ – Дніпропетровський металургійний комбінат; В₂ – Запорізький металургічний комбінат (Запоріжсталь); В₃ – Маріупольський металургійній комбінат (Азовсталь); В₄ – Донецький металургійний завод; В₅ – Запорізький завод «Дніпроспецсталь».

В нижній частині кожної клітини наведена вартість перевезення 1т/км вантажу. В роботі розглянута збалансована модель транспортної задачі.

Попередній план перевезень складаємо методом мінімального елементу таблиці (таблиця 2).

Таблиця 2.

Вj Аі	В1=100	В2=150		В3=250	В4=80	В5=120
А1=200	10	8		200 7	12	9	U1=-3
А2=300	100 7	0 9		10	80 13	120 6	U2=0
А3=170	12	120 7		50 8	9	10	U3=-2
А4=30	13	30 6		9	10	12	U4=-3
V1=7		V2=9	V3=10	V4=13	V5=6

Вартість такого плану перевезень складає:

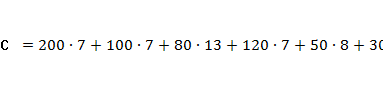(умовних одиниць)

Перевірку плану на оптимальність виконуємо методом потенціалів. Для цього введемо потенціал третього ряду U₂=0. Потенціали рядків та стовпців пов'язані співвідношенням:

U_і + V_j = C_ij (1)

Знайдемо потенціали усіх рядків та стовпців (таблиця 2). Далі знаходимо потенціали незавантажених клітин із співвідношення:

P_ij = U_і + V_j - C_ij (2)

Умова оптимальності плану P_ij£0 (3)

Знайдемо потенціали незавантажених клітин:

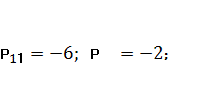
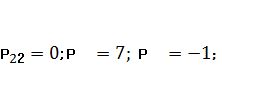
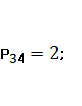
Серед потенціалів незавантажених клітин є додатній потенціал (клітина є потенціалом, Р₃₄=2). Будуємо замкнений цикл та перерозподіляємо вантажі по замкненому циклу:

+ 0 80 –

– 120 +

За алгоритмом методу потенціалів величина вантажу для перерозподілу визначається як min(120,80)=80. Будуємо новий план та перевіряємо його на оптимальність (таблиця 3).

Таблиця 3.

Вj Аі	В1=100	В2=150		В3=250	В4=80	В5=120
А1=200	10	8		200 7	12	9	U1=3
А2=300	100 7	80 9		10	13	120 6	U2=0
А3=170	12	40 7		50 8	80 9	10	U3=-2
А4=30	13	30 6		9	10	12	U4=-3
V1=7		V2=9	V3=10	V4=11	V5=6

;

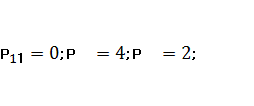
План не оптимальний, так як є клітина з додатнім потенціалом. Будуємо замкнений цикл та перерозподіляємо вантажі по замкненому циклу.

+ 40 160 –

– 0 90 +

Отримаємо новий план перевезень таблиця 4.

Таблиця 4.

Вj Аі	В1=100	В2=150		В3=250	В4=80	В5=120
А1=200	10	40 8		160 7	12	9	U1=8
А2=300	100 7	80 9		0 10	13	120 6	U2=9
А3=170	12	7		90 8	80 9	10	U3=9
А4=30	13	30 6		9	10	12	U4=6
V1=-2		V2=0	V3=10	V4=-1	V5=-3

.

Отримали оптимальний план перевезень, вартість якого складає:

одиниць вартості.

У порівнянні з вартістю попереднього плану перевезень економія складає ~17%. В масштабах державного планування застосування методів математичного програмування вносить вагомий внесок.

Знайомство студентів з можливостями застосування математичного апарату до пошуку оптимальних розв'язків економічних задач збагачує їх інтелект, підвищує якість вищої освіти та якість випускників вищої школи.

Література:

1. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. «Математическое программирование».- М.: Москва. Высшая школа, 1980.

2. Карпелевич Ф.И., Садовский Л.Е. «Элементы линейной алгебры и линейного программирования».- М.: Наука, 1967.