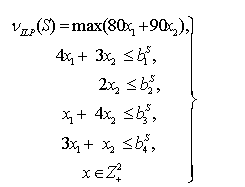Математика/4. Прикладная математика
К.ф.-м.н.
Зинченко А.Б., Саакова В.А.
Южный
федеральный университет. Россия
Клановые и близкие к ним кооперативные игры
Кооперативная игра с трансферабельной полезностью имеет вид ![]() , где
, где ![]() - конечное
множество (игроков, агентов),
- конечное
множество (игроков, агентов), ![]() ,
, ![]() - характеристическая
функция, удовлетворяющая условию
- характеристическая
функция, удовлетворяющая условию ![]() . Значение
. Значение ![]() , называемое весом коалиции
, называемое весом коалиции ![]() , интерпретируется как максимальная выгода, которую может
получить эта коалиция без помощи остальных агентов. Игра
, интерпретируется как максимальная выгода, которую может
получить эта коалиция без помощи остальных агентов. Игра ![]() моделирует ситуации,
участники которых, объединяя ресурсы, капиталы, технологии, доступную информацию
и т.д., могут получить дополнительную полезность: увеличить прибыль, престиж,
влияние на других, сократить расходы. Предполагается, что сформировалась
коалиция
моделирует ситуации,
участники которых, объединяя ресурсы, капиталы, технологии, доступную информацию
и т.д., могут получить дополнительную полезность: увеличить прибыль, престиж,
влияние на других, сократить расходы. Предполагается, что сформировалась
коалиция ![]() всех игроков. Проблема
состоит в "справедливом" распределении общей полезности
всех игроков. Проблема
состоит в "справедливом" распределении общей полезности ![]() между участниками
игры. С-ядро (core) игры
между участниками
игры. С-ядро (core) игры ![]() состоит из эффективных
и коллективно-рациональных векторов индивидуальных выигрышей
состоит из эффективных
и коллективно-рациональных векторов индивидуальных выигрышей
![]() .
.
Игра ![]() , имеющая непустое С-ядро, называется сбалансированной.
, имеющая непустое С-ядро, называется сбалансированной.
Клановые игры [1] были введены для моделирования
взаимодействия между группой ![]() сильных агентов (кланом)
и слабыми агентами, не принадлежащими клану. Коалицию слабых игроков
сильных агентов (кланом)
и слабыми агентами, не принадлежащими клану. Коалицию слабых игроков ![]() называют союзом. Клановая игра
называют союзом. Клановая игра ![]() лиц с коалицией
лиц с коалицией ![]() в качестве клана определяется условиями:
в качестве клана определяется условиями:
(неотрицательность) ![]()
(свойство клана) ![]() (1)
(1)
(свойство союза) ![]() (2)
(2)
Из свойства клана следует, что каждый игрок ![]() имеет право "вето".
Свойство союза означает, что слабые игроки успешней действуют в объединениях,
чем поодиночке. Например, клановой является игра
единогласия (unanimity game)
имеет право "вето".
Свойство союза означает, что слабые игроки успешней действуют в объединениях,
чем поодиночке. Например, клановой является игра
единогласия (unanimity game) ![]() , где
, где ![]() ,
,
в которой выигрывают только те коалиции, которые
содержат фиксированную непустую коалицию ![]() . Такие игры возникают в ситуациях голосования, когда
множество участников содержит группу, имеющую право ²вето², а голоса остальных
агентов несущественны. Если
. Такие игры возникают в ситуациях голосования, когда
множество участников содержит группу, имеющую право ²вето², а голоса остальных
агентов несущественны. Если ![]() , где
, где ![]() , то клановая игра является игрой с максимальным кланом. Только один агент не принадлежит
клану. Если выполняется условие
, то клановая игра является игрой с максимальным кланом. Только один агент не принадлежит
клану. Если выполняется условие ![]() , то клановая игра с нулевым кланом
, то клановая игра с нулевым кланом ![]() сводится к 1-выпуклой
(двойственно симплексной) игре.
сводится к 1-выпуклой
(двойственно симплексной) игре.
Клановая игра, с кланом, состоящим из
одного агента ![]() , известна как немонотонная игра большого босса с игроком
, известна как немонотонная игра большого босса с игроком ![]() в качестве босса.
Монотонная игра большого босса с игроком
в качестве босса.
Монотонная игра большого босса с игроком ![]() в качестве босса [2] определяется
условиями:
в качестве босса [2] определяется
условиями:
(монотонность)
![]() ;
;
(свойство босса) ![]() ; (3)
; (3)
(свойство союза) ![]() .
(4)
.
(4)
Из монотонности игры следует ее неотрицательность и
неотрицательность маргинальных вкладов ![]() всех игроков. Однако
обратное не верно. Кроме монотонных и немонотонных игр большого босса
существуют тотальные (total), обобщенные (generalized) и игры сильного (strong)
большого босса.
всех игроков. Однако
обратное не верно. Кроме монотонных и немонотонных игр большого босса
существуют тотальные (total), обобщенные (generalized) и игры сильного (strong)
большого босса.
Перечислим некоторые приложения
клановых и близких к ним игр: ситуации банкротства и инвестирования,
коллективное страхование, объединение ресурсов для совместного выпуска
продукции, рыночные отношения, дележ прибыли между землевладельцем и наемными
работниками, холдинг.
Клановые и близкие к ним игры обладают привлекательными свойствами:
-
они сбалансированы,
-
С-ядро имеет специальную
структуру, его крайние точки легко вычисляются,
-
существуют простые
критерии выпуклости таких игр,
-
некоторые концепции
решения совпадают, т.е. одновременно отражают несколько принципов
справедливости,
-
неаддитивные в общем
случае решения приобретают для таких игр свойство аддитивности.
Некоторые определения кооперативной теории
не инвариантны относительно стратегической эквивалентности. Например, 0-форма
немонотонной игры может быть монотонной. Не симметричные
игроки могут стать симметричными после 0-нормализации игры. Одна из
стратегически эквивалентных игр может быть инверсионно симметричной, а другая –
нет. Покажем не инвариантность понятий клановой игры и игры большого босса.
Рассмотрим ситуацию производства неделимой
продукции, определенную следующими значениями параметров: ![]() (количество ресурсов);
(количество ресурсов);
![]() (количество типов продукции);
(количество типов продукции);
![]() (количество производителей);
(количество производителей);
![]() - вектор цен;
- вектор цен;
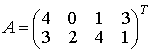 ,
, 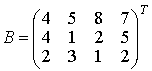
технологическая матрица и матрица ресурсов. Задача,
определяющая вес каждой непустой коалиции S, и векторы ресурсов коалиций имеют вид
|
|
|
|
|
|
|
|
|
Характеристическая функция целочисленной
производственной игры ![]() , а также оптимальные производственные планы приведены во
второй и третьей строках таблицы 1. Игра
, а также оптимальные производственные планы приведены во
второй и третьей строках таблицы 1. Игра ![]() не имеет
вето-игроков, следовательно, не является клановой. Выполнив 0-нормализацию,
получаем игру, приведенную в последней строке таблицы 1. Вычислив маргинальные
вклады игроков
не имеет
вето-игроков, следовательно, не является клановой. Выполнив 0-нормализацию,
получаем игру, приведенную в последней строке таблицы 1. Вычислив маргинальные
вклады игроков
![]() ,
, ![]() ,
, ![]() ,
,
мы видим, что 0-форма игры ![]() монотонна, имеет
вето-игрока и удовлетворяет условию союза, которое для игры трех лиц и
монотонна, имеет
вето-игрока и удовлетворяет условию союза, которое для игры трех лиц и ![]() состоит из одного
неравенства
состоит из одного
неравенства ![]() . Таким образом, в отличие от исходной игры,
0-нормализованная игра
. Таким образом, в отличие от исходной игры,
0-нормализованная игра ![]() есть игра большого
босса с игроком 1 в качестве босса.
есть игра большого
босса с игроком 1 в качестве босса.
Таблица 1
Характеристическая функция производственной игры и ее
0-форма
|
Коалиция |
|
|
|
|
|
|
|
|
|
90 |
80 |
0 |
180 |
180 |
80 |
270 |
|
Вектор выпуска |
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
10 |
90 |
0 |
100 |
Рассмотрим
теперь игру трех лиц ![]() , где
, где
![]()
Игра
не является неотрицательной и не имеет вето-игроков. Это не клановая игра. Однако
после 0-нормализации получаем неотрицательную игру ![]() с характеристической функцией
с характеристической функцией
![]()
неотрицательными
маргинальными вкладами![]()
и
двумя вето-игроками (первым и вторым). Игра ![]() удовлетворяет условию
(2) для CL={1,2}. Следовательно,
удовлетворяет условию
(2) для CL={1,2}. Следовательно, ![]() - клановая игра с коалицией {1,2} в качестве клана.
- клановая игра с коалицией {1,2} в качестве клана.
Следующие два утверждения обобщают рассмотренные
примеры.
Утверждение
1. Игра ![]() , удовлетворяющая (4) и условиям
, удовлетворяющая (4) и условиям
![]() (5)
(5)
![]() (6)
(6)
стратегически эквивалентна монотонной игре большого
босса с игроком ![]() в качестве босса.
в качестве босса.
Доказательство. Игра ![]() стратегически
эквивалентна игре
стратегически
эквивалентна игре ![]() , где
, где
![]() (7)
(7)
Согласно (6), ![]() т.е.
т.е. ![]() удовлетворяет
(3). Из (5) и (7) следует, что
удовлетворяет
(3). Из (5) и (7) следует, что ![]() т.е. игра
т.е. игра![]() монотонная. Если
монотонная. Если ![]() , то из (4) и (7) получаем
, то из (4) и (7) получаем
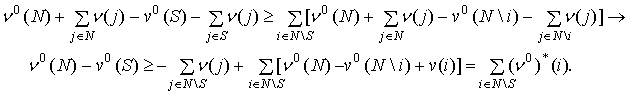
Значит, игра ![]() удовлетворяет (4).
Доказано, что
удовлетворяет (4).
Доказано, что ![]() – монотонная игра
большого босса с игроком
– монотонная игра
большого босса с игроком ![]() в качестве босса. „
в качестве босса. „
Утверждение
2. Пусть ![]() . Игра
. Игра ![]() , удовлетворяющая (2) и условиям
, удовлетворяющая (2) и условиям
![]() (8)
(8)
![]() (9)
(9)
стратегически эквивалентна клановой игре с коалицией CL в
качестве клана.
Доказательство. Рассмотрим стратегически
эквивалентную ![]() игру
игру ![]() , определенную (7). Согласно (8),
, определенную (7). Согласно (8), ![]() для
для ![]() и
и ![]() для
для ![]() . Значит,
. Значит, ![]() – неотрицательная
игра, удовлетворяющая (1). Согласно (9), для всех
– неотрицательная
игра, удовлетворяющая (1). Согласно (9), для всех ![]() справедливо
справедливо
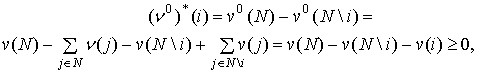
т.е.
маргинальные вклады ![]() неотрицательны для всех
агентов игры
неотрицательны для всех
агентов игры ![]() . Аналогично доказательству утверждения 1, получаем, что
. Аналогично доказательству утверждения 1, получаем, что ![]() удовлетворяет условию
(2). Доказано, что
удовлетворяет условию
(2). Доказано, что ![]() – клановая игра с
коалицией
– клановая игра с
коалицией ![]() в качестве клана.
„
в качестве клана.
„
Множество клановых игр ![]() лиц с кланом
лиц с кланом ![]() и множество игр
большого босса (монотонных и немонотонных) с игроком
и множество игр
большого босса (монотонных и немонотонных) с игроком ![]() в качестве босса обозначим
через
в качестве босса обозначим
через ![]() и
и ![]() соответственно.
Как уже говорилось, клановая игра с одноэлементным кланом является игрой
большого босса (монотонной или не монотонной). Покажем, что существуют клановые
игры, в которых ни один из членов клана не является боссом.
соответственно.
Как уже говорилось, клановая игра с одноэлементным кланом является игрой
большого босса (монотонной или не монотонной). Покажем, что существуют клановые
игры, в которых ни один из членов клана не является боссом.
Рассмотрим неотрицательную игру четырех
лиц с характеристической функцией
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() для остальных
для остальных ![]() .
.
Маргинальные вклады игроков неотрицательны
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Для ![]() выполняется свойство
клана (1) и условие союза (2), т.к.
выполняется свойство
клана (1) и условие союза (2), т.к.
![]() ,
,
а для ![]() -элементных коалиций неравенства из (2) имеют вид
-элементных коалиций неравенства из (2) имеют вид ![]() , т.е. всегда выполняются. Таким образом, данная игра –
клановая и мощность клана больше двух. Очевидно, что первый и второй агенты являются
вето-игроками, т.е. для kÎ{1,2} выполняется условие (3). Однако ни игрок 1, ни
игрок 2 не является боссом, т.к. не выполняются неравенства
, т.е. всегда выполняются. Таким образом, данная игра –
клановая и мощность клана больше двух. Очевидно, что первый и второй агенты являются
вето-игроками, т.е. для kÎ{1,2} выполняется условие (3). Однако ни игрок 1, ни
игрок 2 не является боссом, т.к. не выполняются неравенства
![]() ,
, ![]()
из условия (4).
Возникает
вопрос: существуют ли клановые игры ![]() , с мощностью клана
, с мощностью клана ![]() , которые принадлежат хотя бы одному из классов
, которые принадлежат хотя бы одному из классов ![]() , для
, для ![]() ? Положительный ответ следует из [3], где доказано, что игры
единогласия двухэлементных коалиций
? Положительный ответ следует из [3], где доказано, что игры
единогласия двухэлементных коалиций ![]() являются клановыми
играми с кланом
являются клановыми
играми с кланом ![]() , а также играми большого босса с каждым из игроков
, а также играми большого босса с каждым из игроков ![]() в качестве босса.
Более двух боссов клановая игра
в качестве босса.
Более двух боссов клановая игра ![]() иметь не может.
иметь не может.
Принадлежность
одноточечных решений ![]() -ядру игры
-ядру игры ![]() считается
их положительным свойством, а идеальным -
случай, когда
считается
их положительным свойством, а идеальным -
случай, когда ![]() -ядро состоит
из единственного дележа. Тем не менее, С-ядра клановых и близких к ним игр иногда
содержат контр-интуитивные дележи. Выигрыш
члена клана может быть нулевым, в то время как малого игрока – максимально
возможным в С-ядре. И наоборот, вся прибыль от кооперации распределяется между
членами клана (или достается боссу). Численный эксперимент показывает, что в
клановой игре ненулевые игроки часто получают нулевые выигрыши. В таких играх
значение Шепли (при бездотационном принципе распределения благ) и консенсус-значение
[4] (при компенсационном принципе) более согласованы с экономическими
ситуациями, порождающими клановые игры, чем дележи из
-ядро состоит
из единственного дележа. Тем не менее, С-ядра клановых и близких к ним игр иногда
содержат контр-интуитивные дележи. Выигрыш
члена клана может быть нулевым, в то время как малого игрока – максимально
возможным в С-ядре. И наоборот, вся прибыль от кооперации распределяется между
членами клана (или достается боссу). Численный эксперимент показывает, что в
клановой игре ненулевые игроки часто получают нулевые выигрыши. В таких играх
значение Шепли (при бездотационном принципе распределения благ) и консенсус-значение
[4] (при компенсационном принципе) более согласованы с экономическими
ситуациями, порождающими клановые игры, чем дележи из ![]() -ядра.
-ядра.
Литература:
1. Potters J., Poos R., Tijs S., Muto S. Clan games // Games and
Economic Behavior. 1989. № 1. P. 275-293.
2.
Muto S., Nakayama M., Potters J.,
Tijs S. On big boss games // The Economic Studies Quarterly. 1988. № 39. P.
303-321.
3. Zinchenko A.B. Polytopes of special classes of the balanced transferable utility games
// Journal of Applied and Industrial Mathematics.
2016. Vol. 10. No. 1. P. 145-154.
4. Ju Y., Born P., Rays P. The consensus value: a new solution
concept for cooperative games // Social Choice and Welfare. 2006. Vol. 28. № 4. P. 85-703.