Математика /5. Математическое моделирование
К.т.н. Кадникова О.Ю., к.ф.-м.н. Шалдыкова Б.А.
Рудненский индустриальный институт, Республика Казахстан
Применение математического
моделирования для оценки качества пряжи
Рост благосостояния людей, увеличение доходов
трудящихся, все более полное обеспечение спроса на изделия и товары народного
потребления закономерно сопровождаются постоянным повышением требований к их
качеству. Поэтому систематическое улучшение качества товаров народного
потребления становится постоянной и наиболее актуальной задачей, решение
которой должно осуществляться непрерывно и с наибольшей эффективностью. Качество
продукции обуславливается свойствами исходного сырья, надлежащим
технологическим процессом, структурой продукта, его свойствами.
Выбор номенклатуры, определяющих показателей
качества – это первый и наиболее важный этап оценки качества продукции, так как
от результатов его реализации зависит качество исходного сырья, а затем и
готовой продукции. Не менее важным является рациональность требований
потребителя, правильность и достоверность результатов оценки показателей качества,
зависящие от принятых методов оценки. В трикотажном производстве необходимо,
чтобы пряжа при петлеобразовании отличалась мягкостью, прочностью, минимальным
содержанием пороков. Существующие производственные линии по производству
шерстяной и смешанной пряжи не отвечают в полной мере необходимым требованиям
для трикотажного производства [1].
Следовательно, целесообразно проводить комплексную оценку качества нити, а полученные
результаты обрабатывать математическими методами.
В данной работе проведено исследование качества
нитей и пряжи из шерстяного и смешанного волокна с применением корреляционного
анализа.
В практике использования
теории корреляций, особенно в трикотажном производстве, большую роль играет
оценка близости корреляционной зависимости между Х и У к линейной
функциональной зависимости. Близость к
линейной функции возникает в корреляционной зависимости всякий раз, когда
каждая из случайных величин Х и У по отдельности следует нормальному закону
распределения [2,4].
Для количественной оценки
связи между случайными величинами в корреляционном анализе наиболее часто
используют коэффициент корреляции, корреляционное отношение, показатель
корреляции рангов, множественные коэффициенты корреляции и корреляционные
отношения.
Определяют коэффициент
корреляции по формуле:
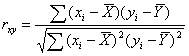(1)
где Xi и Yi -значения случайных величин, между
которыми исследуется корреляционная связь; 
и 
-
средние значения.
Реальный смысл коэффициента
корреляции заключается в том, что его величина выражает отношение числа
факторов, общих для изучаемых случайных величин, ко всему числу факторов,
вызывающих появление данных значений случайных величин [3]. Чем ближе это отношение к единице, тем с большим основанием
можно говорить об одинаковой обусловленности появления изучаемых случайных
величин, т.е. тем теснее между ними корреляционная связь.
Неравномерность волокон по их свойствам,
нестабильность процессов производства пряжи и другие причины вызывают неровноту
продуктов прядения по толщине, прочности и другим свойствам. Источники
неровноты имеются на всем протяжении технологического процесса получения пряжи
– от выбора сырья и составления смески до прядильной машины. Поэтому неровнота по толщине во многих случаях
является определяющим при оценке качества пряжи. Кроме этого, неровнота по
толщине является первопричиной неравномерности других показателей: разрывной
нагрузки, удлинения при разрыве, крутки и т.д. Из
– за неровноты продуктов прядения увеличивается обрывность и, следовательно,
снижается производительность оборудования, ухудшаются свойства и внешний вид
трикотажа.
Поэтому испытания в первую очередь
проводились для исследования неровноты по линейной плотности. Для проведения
исследования были отобраны по одному образцу нитей длиной 10 м из 10 партий и
проведены измерения их массы, диаметра и линейной плотности. Результаты
измерений исследуемого материала сведены в таблицу 1.
Таблица 1 – Значения исследуемых характеристик
|
Показатели |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Масса, m, (г) |
0,598 |
0,566 |
0,572 |
0,642 |
0,608 |
0,609 |
0,617 |
0,615 |
0,573 |
0,704 |
|
Линейная плотность, Т, (г/км) |
56,5 |
55,4 |
59,3 |
59,8 |
62,3 |
61,4 |
60,8 |
61,3 |
56,8 |
68,3 |
|
Диаметр, d, (мм) |
0,272 |
0,264 |
0,260 |
0,284 |
0,279 |
0,275 |
0,276 |
0,280 |
0,268 |
0,299 |
Порядок расчета коэффициента
корреляции между массой и линейной плотностью по формуле (1) показан в таблице 2.
Таблица 2 - Расчет коэффициента корреляции
|
№ |
|
|
|
|
|
|
|
|
1 |
0,598 |
56,5 |
-0,012 |
-3,69 |
0,00014 |
13,6161 |
0,04428 |
|
2 |
0,566 |
55,4 |
-0,044 |
-4,79 |
0,00194 |
22,9441 |
0,21076 |
|
3 |
0,572 |
59,3 |
-0,038 |
-0,89 |
0,00144 |
0,7921 |
0,03382 |
|
4 |
0,642 |
59,8 |
0,032 |
-0,39 |
0,00102 |
0,1521 |
0,01248 |
|
5 |
0,608 |
62,3 |
-0,002 |
2,11 |
0,00001 |
4,4521 |
0,00422 |
|
6 |
0,609 |
61,4 |
-0,001 |
1,21 |
0,0000 |
1,4641 |
0,00121 |
|
7 |
0,617 |
60,8 |
0,007 |
0,61 |
0,00005 |
0,3721 |
0,00427 |
|
8 |
0,615 |
61,3 |
0,005 |
1,11 |
0,00003 |
1,2321 |
0,00555 |
|
9 |
0,573 |
56,8 |
-0,037 |
-3,39 |
0,00137 |
11,4921 |
0,12543 |
|
10 |
0,704 |
68,3 |
0,094 |
8,11 |
0,00884 |
65,7721 |
0,76234 |
|
∑ |
6,104 |
601,9 |
- |
- |
0,01484 |
122,289 |
1,20436 |
|
|
0,610 |
60,19 |
|
|
|
|
|
.
.
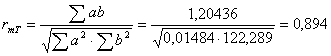Коэффициент корреляции
достаточно высокий, что свидетельствует о существенной зависимости линейной
плотности от массы нити. Близость коэффициента корреляции к единице
свидетельствует о тесной положительной связи между массой и
ее линейной плотностью. Коэффициент детерминации показывает, что величина
линейной плотности объясняется величиной массы только на 79,924%.
Найдем уравнение регрессии между массой
и линейной плотностью:
, 
,
, 
,
b=0,894·3,686/0,041=80,373, a=60,19-80,373·0,61= 11,162.
Тогда уравнение регрессии
имеет вид: y=11,162+80,373x.
Взаимосвязь между массой и линейной плотностью нитей прямая, сильная и положительная. Коэффициент
регрессии b
показывает, что в среднем с увеличением
массы нити на 1 грамм линейная плотность увеличивается на 80,373 г/км.
Аналогичным образом была
исследована связь между диаметром и линейной плотностью. Получены следующие
результаты:
, 
, 
,
, 
,
b=277,081, a=-16,284.
y=-16,284+277,081x - уравнение регрессии.
С увеличением диаметра на 1 мм линейная плотность
возрастает в среднем на 277,081 г/км. Тесноту
линейной связи между показателями оценили с помощью коэффициент корреляции 
, значение
которого подтверждает наличие сильной связи между диаметром и линейной
плотностью. Взаимосвязь между исследуемыми
показателями приведена на рисунках 1 и 2.
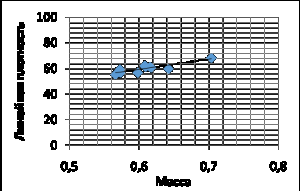
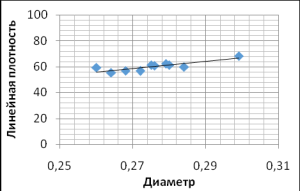
а) б)
Рисунок 1 -
Взаимосвязь между: а) массой и линейной плотностью;
б) диаметром и
линейной плотностью
Результаты корреляционно-регрессионного
анализа показывают, что исследуемая пряжа отличается по коэффициенту вариации и
неравномерности по линейной плотности. Исследуемые нити имеют толстые и тонкие
места. Именно эти колебания по толщине вызывают колебания по прочности. Тем не менее,
исследуемая пряжа соответствует стандартным значениям.
Литература:
1. Кадникова О.Ю. Исследование влияния влажно-тепловой
обработки на свойства пряжи повторного использования.: Наука 21 века: вопросы, гипотезы,
ответы. 2013. № 2.
С. 91-95
2. Кремер, Н.Ш. Теория вероятностей и
математическая статистика.: Учеб. для вузов/ Н.Ш. Кремер
- М.: ЮНИТИ-ДАНА, 2004.
3. Елисеева,
И.И. Эконометрика.: Учебник/ И.И. Елисеевой, С.В. Курышева, Т.В. Костеева и др –
М.: Финансы и статистика, 2007.
4. Виноградов, Ю.С. Математическая
статистика и ее применение в текстильной и швейной промышленности./ Ю.С. Виноградов – М.: Легкая индустрия, 1970.