Пиль Э.А.

Академик РАЕ, профессор, доктор технических наук,

г. Санкт-Петербург

влияние шести переменных на площадь SSeu

Ниже представлена статья, в которой рассмотрены двенадцать вариантов влияния шести переменных на параметр существования площади SSeu. Построенные кривые SSeu позволяют наглядно представить влияние на нее этих переменных. При этом переменные могут увеличиваться, уменьшаться и быть постоянными. Таким образом, в предлагаемой статье рассмотрены зависимости изменения SSeu= f(Х1, Х2, Х3, Х4, Х5, Х6).

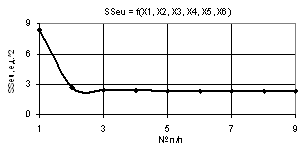
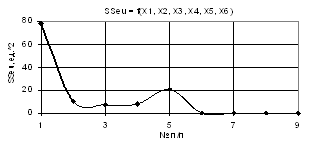
На первом рис. 1 изображена зависимость SSeu при Х1 =Х2 = 1,Х3 = 1..10, Х4 = Х5 = 1...0.1, Х6 = 0.1…1. Из этого примера видно, что параметр SSeu падает до минимума 7,23 в точке 3 после чего увеличивается до 20,78 и потом падает до нуля.

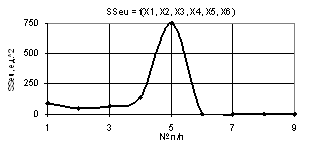
Рис. 1. SSeu = f(X1, X2, X3, Х4, Х5, Х6) Х1 =Х2 = 1,Х3 =1..10, Х4 = Х5=1..0.1,Х6 = 0.1..1	Рис. 2. SSeu = f(X1, X2, X3, Х4, Х5, Х6) Х1 =Х2 = 1,Х3 =Х4 = Х5=1..0.1,Х6 = 0.1..1
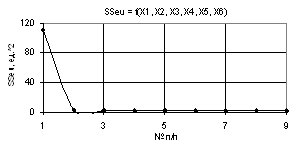
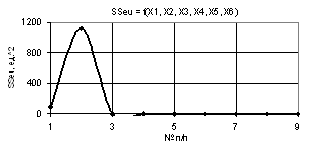
Рис. 3. SSeu = f(X1, X2, X3, Х4, Х5, Х6) Х1= Х6 =1, Х2= Х4 = 1…0.1, Х3= Х5= 1..10	Рис. 4. SSeu = f(X1, X2, X3, Х4, Х5, Х6) Х1= Х6 =1, Х2= 1..10, Х3= Х5= 0.1…1, Х4 =0.1..1

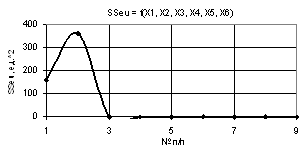
Следующий рис. 2 показывает, что при значениях переменных Х1 =Х2 = 1, Х3 = Х4 = Х5 = 1...0.1, Х6 = 0.1…1 параметр SSeu также падает до минимума 45,18 в точке 2, а после растет до 750,22 в точке 5 и падает до нуля в точке 6.

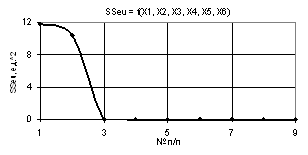
На следующих двух рисунках 3 и 4 показаны зависимости SSeu = f(X1, X2, X3, Х4, Х5, Х6), когда переменные были Х1 = Х6 = 1, Х2 = Х4 = 1…0.1, Х3 = Х5 = 1...10 и Х1 = Х6 = 1, Х2 = 1...10, Х3 = Х5 = 0.1…1, Х4 = 0.1…1. Здесь значения параметра SSeu на рис. 3 падают с 111,51 до 2,63 в точке 2 и далее уменьшается очень медленно. На рис. 4 параметр SSeu достигает максимума 1127,33 в точке 2 и падает до нуля в точке 3.

Рис. 5. SSeu = f(X1, X2, X3, Х4, Х5, Х6) Х1= Х6 =1, Х2= Х4= 0.1…1,Х3= 1…0.1,Х5=1..10		Рис. 6. SSeu = f(X1, X2, X3, Х4, Х5, Х6) Х1= Х6 =1, Х2= Х3= 1…10,Х4= Х5=1…0.1
Рис. 7. SSeu = f(X1, X2, X3, Х4, Х5, Х6) Х1= Х6 =1, Х2= Х5= 1…0.1,Х3=1…10,Х4=0.1..1	Рис. 8. SSeu = f(X1, X2, X3, Х4, Х5, Х6) Х1= Х6 =1, Х2= Х5= 1…10,Х3= Х4=1…0.1

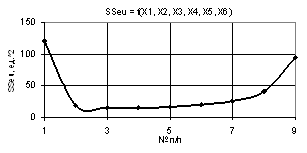
Следующие два рисунка 5 и 6 были построены при Х1= Х6 =1, Х2 = Х4 = 0.1…1, Х3 = 1…0.1, Х5 = 1...10 и Х1 = Х6 = 1, Х2 = Х3 = 1…10, Х4 = Х5 = 1…0.1. Из рисунка 5 видно, что параметр SSeu резко падает с 8,43 до 2,69 в точке 2 и далее медленно уменьшается. Кривая, представленная на рис. 6 быстро возрастает с 159 до 362 в точке 2 и падает до нуля в точке 3.

Для построения двух 2D графиков на рис. 7 и 8 были использованы следующие значения переменных: Х1 = Х6 = 1, Х2 = Х5 = 1…0.1, Х3 = 1…10, Х4 = 0.1...1 и Х1 = Х6 = 1, Х2 = Х3 = 1…10, Х4 = Х5 = 1…0.1. На рис. 7 построенная кривая SSeu резко уменьшается и в точке 3 равна нулю. Из рис. 8 видно, что построенная кривая имеет минимум 14,94 в точке 4 после чего растет до 94,20.

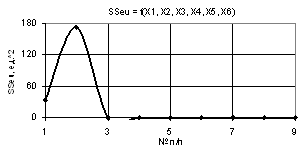
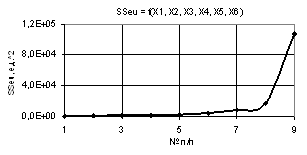
Из следующего рис. 9 видно, что кривая SSeu имеют максимум 173,12 в точке 2 и падает до нуля в точке 3. Построенная же на рис. 10 кривая вырастает до значительной величины 1,07Е+05 в точке 9.

Рис. 9. SSeu = f(X1, X2, X3, Х4, Х5, Х6) Х1= Х6 =1, Х2= Х3= 1…10,Х4=0.1…1,Х5= 1..0.1		Рис. 10. SSeu = f(X1, X2, X3, Х4, Х5, Х6) Х1= Х3= 1..0.1, Х2= 1…10, Х4=0.1..1, Х5= Х6 =1
Рис. 11. SSeu = f(X1, X2, X3, Х4, Х5, Х6) Х1= Х2= 1..0.1, Х3= 1…10, Х4=0.1..1, Х5= Х6 =1	Рис. 12. SSeu = f(X1, X2, X3, Х4, Х5, Х6) Х1= Х2= 1…10, Х3= Х4=1…0.1, Х5= Х6 =1

На последних двух рисунках 11 и 12 были построены две кривые SSeu при Х1 = Х2 = 1...0.1, Х3 = 1…10, Х4 = 0.1…1, Х5 = Х6 = 1 и Х1 = Х2 = 1…10, Х3 = Х4 = 1…0.1, Х5 = Х6 = 1 соответственно.

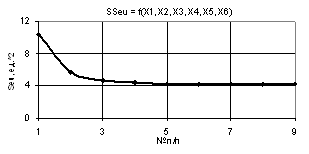
Здесь из рис. 11 видно, что кривая падает с 10,42 до 4,38 в точке 4, а после уменьшается очень медленно до 4,182.

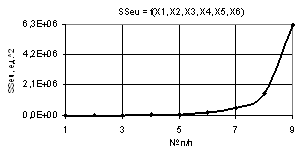
На рис. 12 параметр SSeu достигает самого большого своего значения 6,24Е+06 из всех рассчитанных ранее.